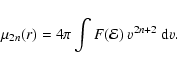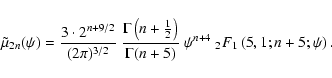Up: The Hernquist model revisited:
Subsections
The simplest dynamical models are those where the augmented
density is a function of the potential only,
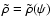 .
For such models, the
distribution function is only a function of the binding energy,
i.e. the distribution function is isotropic. In this case, the
integral Eq. (1) can be inverted to find the
well-known Eddington relation
.
For such models, the
distribution function is only a function of the binding energy,
i.e. the distribution function is isotropic. In this case, the
integral Eq. (1) can be inverted to find the
well-known Eddington relation
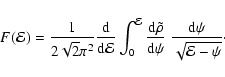 |
(12) |
For such isotropic models, we do not use the general anisotropic
moments (6), but define the isotropic moments as
 |
(13) |
Similarly as for the anisotropic moments, we can derive a relation
that allows to calculate the augmented isotropic moments from the
augmented density
 .
Indeed, they satisfy the
relation (Dejonghe 1986)
.
Indeed, they satisfy the
relation (Dejonghe 1986)
 |
(14) |
In particular, we obtain an expression for the velocity dispersion
profile by setting n=1,
 |
(15) |
The isotropic model that corresponds to the potential-density pair (2ab)
is described in full detail by Hernquist (1990).
We restrict ourselves by resuming the most important results, for
a comparison with the anisotropic models discussed later in this
paper. The augmented density reads
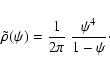 |
(16) |
Substituting this density into Eddington's formula (12)
yields the distribution function
![$\displaystyle F({\cal{E}})
=
\frac{1}{8\sqrt{2}\pi^3}
\left[
\frac{\sqrt{{\cal{...
...cal{E}})^2}
+
\frac{3\arcsin\sqrt{{\cal{E}}}}{(1-{\cal{E}})^{5/2}}
\right]\cdot$](/articles/aa/full/2002/38/aa2799/img63.gif) |
|
|
(17) |
Combining the density (16) with the general formula (14)
gives us the moments of the distribution
function,
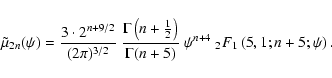 |
(18) |
For all
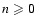 ,
this expression can be written in terms of
rational functions and logarithms. For example, for the velocity
dispersions, we obtain after substitution of the Hernquist
potential (2a),
,
this expression can be written in terms of
rational functions and logarithms. For example, for the velocity
dispersions, we obtain after substitution of the Hernquist
potential (2a),
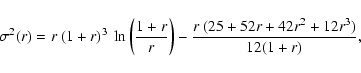 |
(19) |
in agreement with Eq. (10) of Hernquist (1990). From an
observational point of view, it is very useful to obtain an
explicit expression for the line-of-sight velocity dispersion. For
isotropic models, the line-of-sight dispersion is easily found by
projecting the second-order moment on the plane of the sky, i.e.
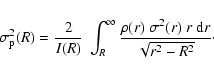 |
(20) |
For the Hernquist model this yields after some algebra


Up: The Hernquist model revisited:
Copyright ESO 2002
![]() .
For such models, the
distribution function is only a function of the binding energy,
i.e. the distribution function is isotropic. In this case, the
integral Eq. (1) can be inverted to find the
well-known Eddington relation
.
For such models, the
distribution function is only a function of the binding energy,
i.e. the distribution function is isotropic. In this case, the
integral Eq. (1) can be inverted to find the
well-known Eddington relation