

Up: The Hernquist model revisited:
A general discussion on the inversion of the fundamental Eq. (1),
and hence on the construction anisotropic
distribution functions for a given spherical potential-density
pair, is presented by Dejonghe (1986). The key ingredient of the
inversion procedure is the concept of the augmented mass density
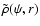 ,
which is a function of potential and
radius, such that the condition
,
which is a function of potential and
radius, such that the condition
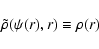 |
(5) |
is satisfied. The augmented mass density is in fact equivalent to
the distribution function
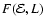 :
with every augmented
density
:
with every augmented
density
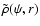 we can associate a distribution
function
we can associate a distribution
function
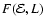 and vice versa. There exist various
transition formulae between these two equivalent forms of a
dynamical model, amongst others a formalism that uses combined
Laplace-Mellin transforms.
and vice versa. There exist various
transition formulae between these two equivalent forms of a
dynamical model, amongst others a formalism that uses combined
Laplace-Mellin transforms.
Besides providing a nice way to generate a distribution function
for a given potential-density pair, the augmented density is also
very useful to calculate the moments of the distribution function.
The anisotropic moments are defined as
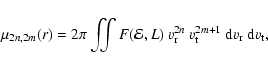 |
(6) |
where
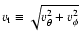 is the transverse
velocity. One can derive a relation that links the higher-order
moments to the augmented mass density
is the transverse
velocity. One can derive a relation that links the higher-order
moments to the augmented mass density
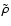 ,
when written
explicitly as a function of
,
when written
explicitly as a function of 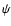 and r,
and r,
![$\displaystyle \tilde{\mu}_{2n,2m}(\psi,r)
=
\frac{2^{m+n}}{\sqrt{\pi}}~
\frac{\...
...m}}{({\rm d}r^2)^{m}}
\left[
r^{2m}~\tilde{\rho}(\psi',r)
\right]
{\rm d}\psi'.$](/articles/aa/full/2002/38/aa2799/img47.gif) |
|
|
(7) |
In particular, the radial and transverse velocity dispersions can
be found from the density through the relations, 010
By means of these functions, we can define the anisotropy
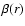 as
as
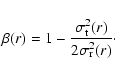 |
(9) |
We will in this paper consider augmented densities which are
separable functions of 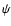 and r, and we introduce the
notation
and r, and we introduce the
notation
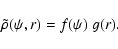 |
(10) |
For such models, the anisotropy can be directly calculated from
the augmented density as
![\begin{displaymath}\beta(r)
=
1-\frac{1}{g(r)}~\frac{{\rm d}}{{\rm d}r^2}
\left[r^2~g(r)\right],
\end{displaymath}](/articles/aa/full/2002/38/aa2799/img55.gif) |
(11) |
as a result of the formulae (8ab), (9)
and (10).


Up: The Hernquist model revisited:
Copyright ESO 2002
![]() ,
which is a function of potential and
radius, such that the condition
,
which is a function of potential and
radius, such that the condition
![]() as
as