From a stellar dynamical point of view, the most complete
description of a stellar system is the distribution function
![]() ,
which gives the probability density for the stars
in phase space. In this paper, we will concentrate on the problem
of constructing anisotropic equilibrium distribution functions
that self-consistently generate a given spherical mass density
profile
,
which gives the probability density for the stars
in phase space. In this paper, we will concentrate on the problem
of constructing anisotropic equilibrium distribution functions
that self-consistently generate a given spherical mass density
profile ![]() .
In the assumption of spherical symmetry, the
mass density of a stellar system can easily be derived from the
observed surface brightness profile, at least if we assume that
the mass-to-light ratio is constant and that dust attenuation is
negligible. And as the surface brightness of a galaxy (or bulge or
cluster) is fairly cheap and straightforward to observe, compared
to other dynamical observables which require expensive
spectroscopy, the problem we will deal with is relevant and
important.
.
In the assumption of spherical symmetry, the
mass density of a stellar system can easily be derived from the
observed surface brightness profile, at least if we assume that
the mass-to-light ratio is constant and that dust attenuation is
negligible. And as the surface brightness of a galaxy (or bulge or
cluster) is fairly cheap and straightforward to observe, compared
to other dynamical observables which require expensive
spectroscopy, the problem we will deal with is relevant and
important.
The first step in the construction of self-consistent models is
the calculation of the gravitational potential ![]() ,
which
can immediately be determined through Poisson's equation. The
second step, the actual construction of the distribution function,
is less straightforward. Basic stellar dynamics theory (see e.g. Binney & Tremaine 1987) learns that steady-state distribution
functions for spherical systems can generally be written as a
function of binding energy and angular momentum. We hence have to
determine a distribution function
,
which
can immediately be determined through Poisson's equation. The
second step, the actual construction of the distribution function,
is less straightforward. Basic stellar dynamics theory (see e.g. Binney & Tremaine 1987) learns that steady-state distribution
functions for spherical systems can generally be written as a
function of binding energy and angular momentum. We hence have to
determine a distribution function
![]() ,
such that the
zeroth order moment of this distribution function equals the
density, i.e. we have to solve the integral equation
,
such that the
zeroth order moment of this distribution function equals the
density, i.e. we have to solve the integral equation
Particularly interesting are models for which the distribution function and its moments can be computed analytically. Such models have many useful applications, which can roughly be divided into two classes. On the one hand, they can improve our general understanding of physical processes in galaxies in an elegant way. For example, they can serve as simple galaxy models, in which it is easy to generate the starting conditions for N-body or Monte Carlo simulations, or to test new data reduction or dynamical modelling techniques. A quick look at the overwhelming success of simple analytical models, such as the Plummer sphere (Plummer 1911; Dejonghe 1987), the isochrone sphere (Hénon 1959, 1960), the Jaffe model (Jaffe 1983) and the Hernquist model (Hernquist 1990), provides enough evidence. On the other hand, analytical models are also useful for the detailed dynamical modelling of galaxies. For example, in modelling techniques such as the QP technique (Dejonghe 1989), a dynamical model for an observed galaxy is built up as a linear combination of components, for each of which the distribution function and its moments are known analytically. As a result, the distribution function and the moments of the final model are also analytical, which obviously has a number of advantages.
Unfortunately, the number of dynamical models for which the distribution function is known analytically is rather modest. Moreover, most of them consist of distribution functions that are isotropic or of the Osipkov-Merritt type, and therefore basically one-dimensional. An exception is the completely analytical family of anisotropic models described by Dejonghe (1987). These models self-consistently generate the Plummer potential-density pair, a simple yet useful model for systems with a constant density core.
During the last decade, however, it has become clear that, at
small radii, elliptical galaxies usually have central density
profiles that behave as
![]() with
with
![]() (Lauer et al. 1995; Gebhardt et al. 1996). Such galaxies can
obviously not be adequately modelled with a constant density core.
This has stimulated the quest for simple potential-density pairs,
and corresponding distribution functions, with a central density
cusp. The first effort to construct such models was undertaken by
Ciotti (1991) and Ciotti & Lanzoni (1997), who discussed the the
dynamical structure of stellar systems following the R1/m law
(Sérsic 1968), a natural generalization of the empirical
R1/4 law of de Vaucouleurs (1948). A major drawback of this
family, however, is that the spatial density and the distribution
function can not be written in terms of elementary functions (see
Mazure & Capelato 2002). A more useful family is formed by the
so-called
(Lauer et al. 1995; Gebhardt et al. 1996). Such galaxies can
obviously not be adequately modelled with a constant density core.
This has stimulated the quest for simple potential-density pairs,
and corresponding distribution functions, with a central density
cusp. The first effort to construct such models was undertaken by
Ciotti (1991) and Ciotti & Lanzoni (1997), who discussed the the
dynamical structure of stellar systems following the R1/m law
(Sérsic 1968), a natural generalization of the empirical
R1/4 law of de Vaucouleurs (1948). A major drawback of this
family, however, is that the spatial density and the distribution
function can not be written in terms of elementary functions (see
Mazure & Capelato 2002). A more useful family is formed by the
so-called ![]() -models (Dehnen 1993; Tremaine et al. 1994),
characterized by a density proportional to r-4 at large radii
and a divergence in the center as
-models (Dehnen 1993; Tremaine et al. 1994),
characterized by a density proportional to r-4 at large radii
and a divergence in the center as
![]() with
with
![]() .
The dynamical structure of models with this
potential-density pair has been extensively investigated (e.g. Carollo et al. 1995; Ciotti 1996; Meza &
Zamorano 1997), but only for isotropic or Osipkov-Merritt type
distribution functions. Simple analytical models with a more
general anisotropy structure are still lacking.
.
The dynamical structure of models with this
potential-density pair has been extensively investigated (e.g. Carollo et al. 1995; Ciotti 1996; Meza &
Zamorano 1997), but only for isotropic or Osipkov-Merritt type
distribution functions. Simple analytical models with a more
general anisotropy structure are still lacking.
In this paper we construct a number of families of completely
analytical anisotropic dynamical models that self-consistently
generate the Hernquist (1990) potential-density pair. It is a
special case of the family of ![]() -models, corresponding to
-models, corresponding to
![]() .
In dimensionless units, the Hernquist
potential-density pair is given by 010
.
In dimensionless units, the Hernquist
potential-density pair is given by 010
As the density diverges as 1/r for
![]() ,
the surface
brightness I(R) will diverge logarithmically for
,
the surface
brightness I(R) will diverge logarithmically for
![]() .
More precisely, the surface brightness profile
has the form
.
More precisely, the surface brightness profile
has the form
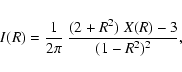 |
(3) |
Copyright ESO 2002