- ...
errors
![[*]](/icons/foot_motif.gif)
- Detailed analysis of the data
will be presented elsewhere (Wozna et al. 2002, in preparation).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... accurate
![[*]](/icons/foot_motif.gif)
- For
presentation of detailed numerical results see e.g. Harding et al. (1997).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... occurs
![[*]](/icons/foot_motif.gif)
- It is easy to reproduce the behaviour of
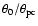 as a function of P in Fig. 7 with analytic formula:
the maximal value of
as a function of P in Fig. 7 with analytic formula:
the maximal value of
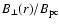 encountered in a static dipolar field by a photon emitted along the local field line at
encountered in a static dipolar field by a photon emitted along the local field line at  is approximately equal to
is approximately equal to
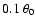 (Sturrock 1971, also Fig. 1
in Rudak & Ritter 1994). This occurs always
at
(Sturrock 1971, also Fig. 1
in Rudak & Ritter 1994). This occurs always
at
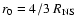 ,
regardless the value of
,
regardless the value of  .
The angle
.
The angle 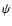 between the photon propagation direction and
the local field line at r0 is
between the photon propagation direction and
the local field line at r0 is
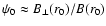 and therefore
and therefore
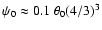 .
To minimize
.
To minimize
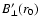 as much as possible in the case of rotation,
the aberration angle due to local linear velocity
as much as possible in the case of rotation,
the aberration angle due to local linear velocity
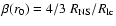 should be close to
should be close to
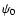 .
Since
.
Since
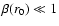 ,
the aberration angle is
,
the aberration angle is
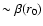 .
Therefore, we obtain the condition
.
Therefore, we obtain the condition
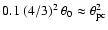 which
gives
which
gives
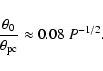 |
(9) |
This formula overestimates the locations of maxima in Fig. 7
by a factor  2 only.
2 only.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.