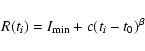 |
(1) |
A large sample of the brightest BATSE GRBs was used with the data
combined from the four energy channels (Fishman & Meegan 1995). The
analysis procedures are described in detail elsewhere (Quilligan
et al. 2002; McBreen et al. 2001, 2002a). The full sample
consisted of 100 GRBs with duration
T90 < 2 s where T90measures the burst integrated count from 5% to 95% of the
total, 319 GRBs with
T90 > 2 s and a further fainter sample
of 79 GRBs with
T90 > 100 s to include very long bursts. The
cumulative light curves of most GRBs could be approximated by a
linear function implying constant output over most of the
duration of the burst (McBreen et al. 2002a). Two significant
minorities were visually identified that are better described by
nonlinear changes in the cumulative count. In category A the
running count increased towards the tallest pulse in the burst
resulting in a nonlinear increase in the cumulative profile. In
category B the running count decreased after the tallest pulse in
the burst causing the cumulative profile to increase at a much
slower rate as time progressed. In category A the normalised
cumulative profile was fit by the function
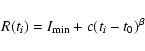 |
(1) |
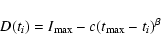 |
(2) |
The median number of pulses N in GRBs with T90 > 2 s is only 6 (Quilligan et al. 2002) and the requirement on N restricts the GRBs to about half of the total. The number of pulses is important because they may originate from explosions in the central engine and discriminate against GRBs, where the emission is not well resolved into pulses because of the washing out of time structure in the jet before the gamma-ray photosphere, and interactions with the external medium including the effects of early afterglow (Dermer & Mitman 1999). The changes in the cumulative count presented here are quite different from the smooth power law decays in GRBs of the FRED (i.e. Fast Rise Exponential Decay) type (Giblin et al. 2002) and the smooth decays in a sample of pulses within GRBs (Ryde & Svensson 2001).
Most GRBs with T90 < 2 s can also be approximated by a linear fit to the cumulative light curve (McBreen et al. 2002a). The GRBs have a median value of N = 2.5 (McBreen et al. 2001) and no short GRBs were found to meet the criteria used for long GRBs.
Copyright ESO 2002