8 An analytical approach to the tidal perturbations

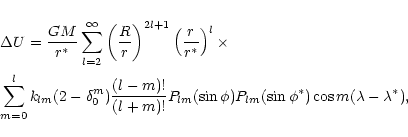
The tidal perturbations of the Moon have various origins:
[1] the Earth deformations due to the Moon;
[2] the Earth deformations due to the Sun;
[3] the deformations of the Moon itself by the Earth;
[4] the deformations of the Moon itself by the Sun.

The main effect arises from [1]. Below, we restrict ourselves to this tidal component. The additional potential of a non rigid Earth acting on the Moon has the well-known classical form (Lambeck 1980):

$$\begin{eqnarray*}&& \Delta U=\frac{GM}{r^*}\sum_{l=2}^{\infty}\left(\frac{R}{r}\... ...P_{lm}(\sin \phi)P_{lm}(\sin \phi^*) \cos m(\lambda-\lambda^*), \end{eqnarray*}$$

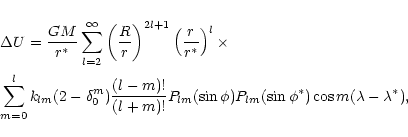
where G is the gravitational constant and M the mass of the Moon, R the equatorial radius of the Earth; l and m are integers. k_l,m are Love numbers and P_l,m Legendre functions. $\lambda$, $\phi$ and r are the spherical coordinates of a point outside of the Earth at time t, in terrestrial axes; $\lambda^{*}$, $\phi^{*}$ and r^* are the same quantities for the Moon's barycenter, the symbol star (*) meaning that the coordinates are evaluated at the time $t^{*} = t - \tau_{l,m}$ where $\tau_{l,m}$ is a delay in the deformation related to the harmonic of index (l,m) attached to the Love number k_l,m. For an elastic Earth: $\tau_{l,m}=0$; in case of an anelastic Earth: $\tau_{l,m}\not=0$. If now we limit ourselves to l=2 and express the above formula in terms of right ascension $\alpha$ and declination $\delta$, we derive for the disturbing function acting on the Earth-Moon vector:

$$\begin{eqnarray*}&& \Delta U=GM\left( 1+\frac{M}{E}\right)\frac{R^5}{{r^*}^3r^3}... ...{22}(\sin\delta^*) \cos(2\alpha-2\alpha^*-2\omega\tau_{22})~], \end{eqnarray*}$$

where $\omega$ is the angular velocity of the Earth, and E is the mass of the Earth. The index (2, 1) induces the diurnal tides; the index (2, 2) induces the semi-diurnal ones.

In the simplified model of the JPL numerical integration DE200 the following approximations where done: k₂₀=k₂₁=k₂₂=k; $\tau_{21}=\tau_{22}=\tau$; $(\omega \tau)^{2}$ is neglected.

In DE245, and further JPL integrations (DE403 and DE405), one simply puts $\tau_{20}=0$, and k₂₁=k₂₂. In the analytical solution ELP we follow the same way, and substitute in $\Delta U$ analytical series for the lunar coordinates. After integration of the differential equations, the main effect consists of two contributions in the mean longitude:

$$\begin{eqnarray*}\Delta W_{1} = a t^{2} + b \cos \Omega. \end{eqnarray*}$$

 

 

Table 8: Contributions of harmonics in the evaluation of a and b coefficients in the lunar mean longitude $\Delta W_{1} = a t^{2} + b \cos \Omega$. k: Love number; $\tau$: time delay.

Parameter	(2, 0)	(2, 1)	(2, 2)	Total
DE200
k	0.30	0.30	0.30
$\tau$ (day)	0	0.006460	0.006460
a ( $''/{\rm cy}^{2}$)		-0.90	-10.55	-11.45
b (10-5'')	0	58	-138	-80
DE403
k	0.34	0.30	0.30
$\tau$ (day)	0	0.014350	0.006772
a ( $''/{\rm cy}^{2}$)		-2.0	-11.06	-13.06
b (10-5'')	0	127	-144	-17
DE405
k	0.34	0.30	0.30
$\tau$ (day)	0	0.012909	0.006942
a ( $''/{\rm cy}^{2}$)		-1.8	-11.34	-13.14
b (10-5'')	0	114	-148	-34

 

 

Table 9: Position angles of the inertial mean ecliptic of J2000.0 with respect to equatorial celestial system (R) in S2001. The uncertainties are formal errors. Units: arcsecond.

R	$\epsilon - 23^{\circ}26'21\arcsec$	$\phi$	$\psi$	Mean Epoch
ICRS	0.41100 $\pm$ 0.00005	-0.05542 $\pm$ 0.00011		Dec. 1994
MCEP	0.40564 $\pm$ 0.00009	-0.01460 $\pm$ 0.00015	0.0445  $\pm$  0.0003	Dec. 1994
DE403	0.40928 $\pm$ 0.00000	-0.05294 $\pm$ 0.00001	0.0048  $\pm$  0.0004	Jan. 1985
DE405	0.40960 $\pm$ 0.00001	-0.05028 $\pm$ 0.00001	0.0064  $\pm$  0.0003	Jan. 1990

The first term corresponds to the secular acceleration $2\times a$. The second term is a periodic term in $\Omega$ with the period of the ascending node of the Moon on the ecliptic (18.6 years).

We gather in Table 8 various evaluations of a and b depending on the model, and the corresponding values of Love numbers and delay. We notice that the b coefficient is smaller in the case of DE403 and DE405 than for DE200. It is mainly due to a partial cancellation of the coefficients arising from (2, 1) and (2, 2), which is not the case for DE200. It should be noted that the value of the secular acceleration ($2\times a$) from Table 8, Col. 5, is not complete as mentioned above. It represents nevertheless the main tidal contributions that are slightly different from the total contributions given in Table 7.

In JPL numerical integrations, Love numbers and time delays are fitted parameters, while in our solution only a is fit. In both cases, because of the long period of the argument $\Omega$, a long and accurate set of data is necessary. Hence, we understand why the value ($2\times a$) of the secular acceleration has been significantly improved since DE200, which was fit on less that 15 years of observations (Williams et al. 1978). A better knowledge of this parameter has benefited from an increasing range of data and an improvement in the quality of observations.