3 Working of the DBNN

The working of the DBNN may be divided into three units. The first unit computes Bayes' probability and the threshold function for each of the training examples. The second unit consists of a gradient descent boosting algorithm that enhances the differences in each of the examples in an attempt to minimize the number of incorrectly classified cases. At this stage, boosting is applied to the connection weights for each of the probability components of the attribute U_m belonging to an example from the class C_k. Initially all the connection weights are set to unity. For the correctly classified object, the total probability , computed as the product of component probabilities will be a maximum for C_k, the class of the object given in the training set. For the wrongly classified examples, for each of the component probability values, the associated weights are incremented by a factor which is proportional to the difference in the total probability of membership of the example in the stated class and that in the wrongly classified class. The exact value is computed as

$$\begin{eqnarray*}\delta W_m = \alpha \left( 1-\frac{P_k} {P^*_k} \right) \end{eqnarray*}$$

in a sequence of iterations through the training set. Here P_k is the computed total probability for the actual class of the object and P^*_k that of the wrongly classified class. The parameter is a learning constant functionally similar to the learning constant in the back-propagation algorithm. It thus defines the rate at which the algorithm updates its weight parameter. The third unit computes the discriminant function (Bishop 1999)  as:

  $$\begin{eqnarray*} P(C_{k}\mid U)=\frac{\prod_{m}\hat{P}(U_{m}\cap C_{k}) W_{m}}{\sum_{j}\prod_{m}\hat{P}(U_{m}\cap C_{j}) W_{m}}\cdot \end{eqnarray*}$$

Here stands for which from the axioms of set theory is equivalent to .

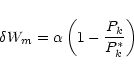
In the implementation of the network, the actual classification is done by selecting the class corresponding to a maximum value for the discriminant function. Since this value is directly related to the probability function, its value is also an estimate of the confidence with which the network is able to do the classification. A low value indicates that the classification is not reliable. Although a network based on back-propagation also gives some probability estimates on the confidence it has on a classification scheme, these are not explicitly dependent on the probabilities of the distribution. Thus while such networks are vulnerable to divergent training vectors that are invariably present in training samples, DBNN is able to assign low probability estimates to such vectors. This is especially significant in astronomical data analysis where one has to deal with variations in the data due to atmospheric conditions and instrumental limitations. Another significance of the approach is the simplicity in the computation. DBNN can be retrained with ease to adapt to the variations in the observations enabling one to generate more accurate catalogs. In the following section, we describe the use of the DBNN technique to differentiate between stars and galaxies in broadband imaging data. We chose to illustrate the capabilities of the DBNN by addressing the star-galaxy classification problem for the following reasons:

1.

A widely used benchmark implementation of the back propagation algorithm is already available for tackling this problem in SExtractor.

2.

High quality imaging data has recently become available from ongoing optical surveys. The number of sources detected by such surveys is large enough for us to construct moderately large training and test sets from uniformly high quality data. The data we use here is publicly accessible and our results can therefore be verified and extended by other researchers.

3.

Construction of a reasonably accurate training set is possible from visual examination, given our experience with optical imaging data.