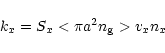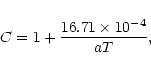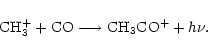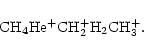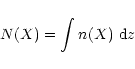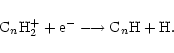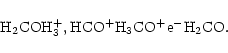A&A 385, 632-646 (2002)
DOI: 10.1051/0004-6361:20020050
Molecular distributions in the inner regions of protostellar disks
A. J. Markwick1 - M. Ilgner2 - T. J. Millar1 - Th. Henning2
1 - Department of Physics, UMIST, Sackville Street,
Manchester M60 1QD, UK
2 -
Astrophysical Institute and University Observatory (AIU),
Friedrich Schiller University, Schillergaesschen 2-3,
07745 Jena, Germany
Received 5 September 2001 / Accepted 10 January 2002
Abstract
The distributions of molecules in the inner regions of a protostellar disk are presented. These were calculated using an uncoupled chemical/dynamical model, with a numerical integration of the vertical disk structure. A comparison between models with and without the effects of X-ray ionisation is made, and molecules are identified which are good tracers of the ionisation level in this part of the disk, notably CN and C2H. In the region considered in this paper (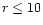 AU), the chemistry is dominated by the thermal desorption of species from grains. This shows that a critically important detail in this region of the disk, as far as molecular distributions are concerned, is the temperature profile. We find that not all of the gaseous material is frozen onto grain surfaces at 10 AU, and we identify species, including some organic molecules, which should exist in observable quantities in the inner regions of protostellar disks.
AU), the chemistry is dominated by the thermal desorption of species from grains. This shows that a critically important detail in this region of the disk, as far as molecular distributions are concerned, is the temperature profile. We find that not all of the gaseous material is frozen onto grain surfaces at 10 AU, and we identify species, including some organic molecules, which should exist in observable quantities in the inner regions of protostellar disks.
Key words: solar system: formation - stars: circumstellar matter -
stars: pre-main sequence - ISM: molecules - ISM: abundances - stars: planetary systems: protoplanetary disks
During star formation, a rotating molecular cloud core undergoes gravitational collapse. The enhanced centripetal effects flatten the protostellar object into an accretion disk. The observational evidence is that most pre-main sequence objects have disks. Since it is thought that planetary systems develop out of contracting molecular clouds, through the accretion disk process, studying the chemistry in these regions is important for the understanding of the connection between interstellar and planetary material.
The complex interdependence of the chemistry, temperature and opacity in the disk gives rise to a set of highly nonlinear equations. Attention has been focused on chemical kinetic models which consider only the midplane of the disk, allowing many simplifications to be made. Some models explicitly follow a parcel of gas from the outer edge to the inner disk, using analytically determined dependencies for quantities in the midplane. Such a model is described in a series of papers emanating from the Heidelberg group (Bauer et al. 1997; Finocchi & Gail 1997; Finocchi et al. 1997; Gail 1998). The model is detailed, including treatments of ice mantle evaporation, dust evaporation, three-body reactions, ionisations by cosmic rays, radionuclides and UV photons and produces interesting results. The most notable of these is that the model (which was set up for the solar nebula) shows peaks in molecules like methane, ammonia and hydrogen sulphide at around 1 AU. The source of the CH4 produced is the carbon resulting from the oxidation of carbon dust grains, and similarly, the H2S is formed from the sulphur which results from the destruction of troilite (FeS) grains. Both dust oxidisation and destruction depend on temperature which means that the temperature profile is the determining factor for this chemical activity. Carbon dust oxidisation starts at around 1000 K, and FeS destruction at around 700 K. Different models using different temperature profiles may exhibit none of this chemical activity around 1 AU, and may give quite different results to the same problem with the same initial conditions.
An approach to chemical modelling along the midplane is to take a complex dynamical code and use values of density, temperature and so on as inputs to a stand-alone chemical model. Such a calculation was presented in Willacy et al. (1998). The disadvantage with this approach is that the dynamics and chemistry are treated as if they are independent, but the (significant) advantage is that both sides of the model (dynamics, chemistry) can be as complex as possible. Willacy et al. report that the chemistry in their model is unlike that of Bauer et al., but this is not surprising because their model has no treatment of dust destruction in it, and even if it did, the midplane temperature profile is different and precludes the possibility of dust being destroyed.
The approach used by Aikawa et al. (1996) is similar to Bauer et al., but their model uses the minimum mass solar nebula model of Hayashi (1981) for the radial dependencies of physical parameters. The model includes adsorption and thermal desorption and neglects dust destruction. Later, Aikawa & Herbst (1999a) augmented the model and calculated the chemistry vertically in three layers; midplane, surface and intermediate. The same authors (1999b, 2001) added deuterium to their chemical model. These models are also based on the minimum mass solar nebula model. Aikawa et al. (1999) present a similar model based on the steady accretion disk model of Lynden-Bell & Pringle (1974). Willacy & Langer (2000) also present a model in which vertical column densities are derived. This time the authors chose to adopt the disk model of Chiang & Goldreich (1997) as the physical input for their calculations. These models present data for the (R,z) distribution of molecules, but they are not 2D models of protostellar disk chemistry. They are 1+1 D models of the type we describe in this work. A 2D coupled chemical/dynamical model of a protostellar disk remains a target for the future.
Comparisons between the various models are difficult because they are all different in the assumptions made and the processes included. This alone means that each model gives different results for the same problem and same initial conditions.
2 Chemistry in protostellar disks
At present, nearby protostellar disks are barely resolved by interferometers (Qi 2000). Radio observations of protostellar disks have detected emission lines of CO (Guilloteau & Dutrey 1994). Dutrey et al. (1997) surveyed other molecular lines around DM Tau and GG Tau. These stars have large disks, extending out to about 800 AU. Molecules detected include CO, CN, CS, HCN, HNC, H2CO, C2H and HCO+. The resolution of current observing facilities precludes the possibility of obtaining detailed spatial information. However, with the advent of submillimetre arrays like ALMA, it will soon be possible for maps of the distributions of molecules in protostellar disks to be made. In this paper, we present an attempt to provide a theoretical comparison for this forthcoming data.
In a typical interstellar cloud model, the input physical parameters are usually the density, temperature, cosmic ray ionisation rate and the visual extinction. They are one point models, which is to say that the values of these parameters are taken to be good for the whole cloud, so the model need only be run once. Where the object in question cannot be treated as one point, or where spatial information is important (as in the case of disks), a trick for calculating the chemistry is to use the values of the physical parameters at each point to run a one point model. A map is soon built up of the abundances at each point. The problem with this approach is clear from the outset - in the vertical direction, each point in the grid evolves in chemical isolation from the others. To implement this method, we need a one point chemical model which is appropriate for an accretion disk, and values of the physical parameters at each grid point.
The method we used to produce the results presented in this paper is based on that of Willacy et al. (1998), except we study the chemistry vertically as well as radially. The structure of the rest of the paper is as follows. In Sects. 3 and 4 we introduce and discuss the modelling approach we have used. Section 3 is concerned with the numerical integration to obtain the vertical disk structure at each radius point, and Sect. 4 describes the chemical model. In Sect. 5 we present contour plots showing the results for 8 molecules listed above. The colour postscript versions of these plots are available for download and printing at http://www.ajmarkwick.com/disks/. We also discuss some aspects of protostellar disk chemistry, involving ionisation processes and gas-grain interaction. Column densities are presented for many molecular species in Sect. 6, and species which could be used to trace physical conditions in the disk are identified. Finally, in Sect. 7 we compare our results at small radii with the previously published studies of molecular distributions at large radii.
3 Vertical disk structure
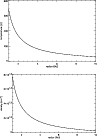 |
Figure 1:
The variation of the midplane temperature (top) and density (bottom), as calculated
by the dynamical model for the protostellar disk described in the text. |
| Open with DEXTER |
The dynamical evolution of a two-dimensional non-self-gravitating disk is characterized
by a set of six partial differential equations for the density, momentum, thermal and
radiation energy. Based on disk dynamics there is a strong evidence for redistribution of
disk material on timescales of 106 years by an angular momentum transfer mechanism.
In contrast to the molecular viscosity the turbulent viscosity may provide an efficient angular
momentum transfer.
The steady-state solution is a simplification of the time-dependent equations of radiation
hydrodynamics mentioned above. Based on these equations one can deduce steady vertical disk
models assuming that the mass transfer rate changes on timescales longer than the viscous
timescale. Separating the radial from the vertical direction leads to 1+1 dimensional disk models
discussed below.
Several models have been presented in the literature to describe the vertical structure of
steady accretion disks (e.g. Meyer & Meyer-Hofmeister 1982; Bell et al. 1997; d'Alessio et al. 1998). Before we introduce the model based on Bell et al. (1997), we briefly review the basic assumptions of current disk models. One assumes no thermal decoupling
between the gas and dust components of the mixture. Assuming hydrostatic equilibrium, the
motion of the gas and dust particles is related to a mean bulk description of motion.
For a given radius r the vertical structure is determined by the following set of coupled
differential equations for the temperature T, the pressure P, and the flux energy density F:
Here 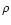 is the mass density, gz is the z-component of the stellar gravity,
is the mass density, gz is the z-component of the stellar gravity, 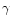 is the gravitational constant and
is the gravitational constant and 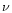 denotes
the kinematic viscosity. Equation (1) is the condition for hydrostatic equilibrium in a
gravitational field. The operator
denotes
the kinematic viscosity. Equation (1) is the condition for hydrostatic equilibrium in a
gravitational field. The operator 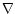 (
(
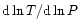 )
has to be specified based on
the favoured energy transport mechanism.
)
has to be specified based on
the favoured energy transport mechanism.
In this work, we assume that the temperature gradients can be caused by convective and
radiative transport. Radiative transport will be the dominant process in regions where the
local temperature gradient of the radiative equilibrium
 is lower than the
adiabatic temperature gradient
is lower than the
adiabatic temperature gradient
 .
Considering radiation transport first, we
use a flux limited diffusion approximation of the radiation transport given by Levermore &
Pomraning (1981). Based on this theory the magnitude of the flux is regulated to be no greater than
the density times the maximum transport speed. In the case that the medium is unstable against
convection the major part of energy transfer is carried by convective elements. This kind
of transport process can be described by mixing length theory. Convective elements will
dissolve and deliver their excess of energy after passing the so-called mixing length. As shown
in Bell et al. (1997) the highest efficiency of the energy transport by convection is in
temperature regions where ice grains exist (
.
Considering radiation transport first, we
use a flux limited diffusion approximation of the radiation transport given by Levermore &
Pomraning (1981). Based on this theory the magnitude of the flux is regulated to be no greater than
the density times the maximum transport speed. In the case that the medium is unstable against
convection the major part of energy transfer is carried by convective elements. This kind
of transport process can be described by mixing length theory. Convective elements will
dissolve and deliver their excess of energy after passing the so-called mixing length. As shown
in Bell et al. (1997) the highest efficiency of the energy transport by convection is in
temperature regions where ice grains exist (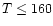 K). The efficiency is around 20% in the
outer parts of the disk. The expressions for the various temperature gradients and related quantities can be found in standard works on stellar atmospheres (e.g. Kippenhahn & Weigert 1994).
K). The efficiency is around 20% in the
outer parts of the disk. The expressions for the various temperature gradients and related quantities can be found in standard works on stellar atmospheres (e.g. Kippenhahn & Weigert 1994).
We assume that the vertical transport of energy is radiated locally. The most dominant energy
production process in the inner parts of the disk is viscous heating. The corresponding energy
flux per unit volume is given by Eq. (3). In the outer parts of the disk,
especially around the disk surface, heating by the stellar radiation field will become the most
dominant heating source (D'Alessio et al. 1998) and has to be taken into account. We limit our considerations to disk radii smaller than 10 AU because for larger radii the disk may prone to gravitational instabilities (see, e.g., Bell et al. 1997). In addition, the disk becomes optically thin and the usual
treatment of the vertical structure breaks down. For the inner part of the disk, only
viscous heating has to be considered.
Assuming vertical thermal balance the energy loss by radiation is exactly balanced by the
local viscous energy production, i.e.:
![\begin{displaymath}\sigma T_{{\rm acc}}^4 = \frac{3}{8 \pi}
\frac{\gamma M_{\as...
...}}{r_{}^3} \left[ 1-\beta \sqrt{\frac{R_{\ast}^{}}{r}}\right],
\end{displaymath}](/articles/aa/full/2002/14/aa1884/img17.gif) |
(4) |
where 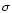 denotes the Stefan-Boltzmann constant and
denotes the Stefan-Boltzmann constant and 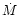 refers to the mass accretion
rate. Setting
refers to the mass accretion
rate. Setting 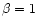 refers to Keplerian orbits with a non-rotating central star. According to Eq. (4), for a central
star with mass
refers to Keplerian orbits with a non-rotating central star. According to Eq. (4), for a central
star with mass 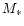 ,
radius
,
radius 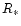 and accretion rate
and accretion rate 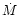 ,
one can calculate the
total energy per unit area radiated at the disk surface as well as the related accretion
temperature. The height of the disk surface corresponds to the assumption of a photosphere
,
one can calculate the
total energy per unit area radiated at the disk surface as well as the related accretion
temperature. The height of the disk surface corresponds to the assumption of a photosphere
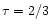 .
Taking into account that in our model viscous heating is the only heating source,
the assumption of a photosphere preserves self-consistently modelling in the sense that according
to the Eddington-Barbier relation the emergent radiation flux is caused approximately by flux
radiated from the photosphere. To calculate the optical depth
.
Taking into account that in our model viscous heating is the only heating source,
the assumption of a photosphere preserves self-consistently modelling in the sense that according
to the Eddington-Barbier relation the emergent radiation flux is caused approximately by flux
radiated from the photosphere. To calculate the optical depth 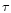 we used approximated formulae
as polynomial fits to the tabulated data of the Rosseland mean opacity
we used approximated formulae
as polynomial fits to the tabulated data of the Rosseland mean opacity
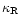 given by Lin
& Papaloizou (1985).
given by Lin
& Papaloizou (1985).
The system of Eqs. (1)-(3) is a two boundary value problem. Based
on a relaxation method we start with a guess of the photospheric thickness (or disk height) determining
the upper boundary condition. Then an inward integration to the midplane is iterated until the
photospheric height is found for which the flux at the midplane vanishes.
We calculated the vertical disk structure for a given mass accretion rate
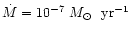 .
The mass of the central object is
.
The mass of the central object is
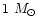 ,
and its radius is
,
and its radius is
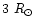 .
The efficiency of viscous transport characterized by
the kinematic viscosity
.
The efficiency of viscous transport characterized by
the kinematic viscosity 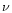 is described by the
is described by the 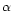 parameterization of Shakura &
Sunyaev (1973) with
parameterization of Shakura &
Sunyaev (1973) with
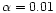 .
Figure 1 shows the variation of the midplane
temperature and density with radius.
.
Figure 1 shows the variation of the midplane
temperature and density with radius.
The disk chemical model is based on that of Willacy et al. (1998) with some modifications described below. The model contains various types of reaction: adsorption, desorption, ion-neutral, neutral-neutral, photoprocesses. Willacy et al. included grain surface reactions, but they are not considered here, since current treatments of them are very uncertain. Termolecular (or three-body) reactions have also been removed, because the rates for these reactions are only valid at temperatures greater than 1000 K. The maximum temperature in the model is  600 K. In addition, Willacy et al. found that their inclusion has only a very small effect.
600 K. In addition, Willacy et al. found that their inclusion has only a very small effect.
Sources of ionisation in the disk include X-ray and UV radiation from the central object, UV from the interstellar radiation field and energetic particles formed by the decay of radioisotopes (see Fig. 2). The latter process is principally from the radioactive decay of 26Al. Briefly, this isotope decays into excited 26Mg by either positron decay or electron capture. In both cases, the excited magnesium isotope de-excites radiatively, releasing a photon of energy 1.809 MeV. This line has in fact been observed in the Galactic Centre (Mahoney et al. 1984). In the case of positron decay, two such positrons can annihilate and form a pair of photons. The ionisation comes from two sources. Either the positron can collisionally ionise material itself, or the photons produced in the decay can Compton scatter their energy into recoil electrons, which can then collisionally ionise the molecules. The net ionisation rate due to this process was found to be
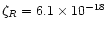 s-1 by Umebayashi & Nakano (1981). An excess of 26Mg was found in the Allende meteorite (Lee et al. 1977), proving that 26Al was present at the time when the meteoritic chrondules formed. 26Al can be produced in AGB stars and ejected during mass loss. Hence we can expect it to be present in protostellar objects.
s-1 by Umebayashi & Nakano (1981). An excess of 26Mg was found in the Allende meteorite (Lee et al. 1977), proving that 26Al was present at the time when the meteoritic chrondules formed. 26Al can be produced in AGB stars and ejected during mass loss. Hence we can expect it to be present in protostellar objects.
X-ray ionisation is only effective near the surface of the disk because the attenuation length of X-rays is small. Observations by X-ray satellites have found that the X-ray luminosity of T Tauri stars is in the range
1028.5-1031.5 erg s-1 (Glassgold et al. 1997). Igea & Glassgold (1999) presented a study of X-ray ionisation in protostellar disks. They found that the ionisation rate in the region
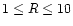 AU is in the range
10-13-10-15 s-1.
AU is in the range
10-13-10-15 s-1.
Aikawa & Herbst (1999a) have calculated the variation of the total ionisation rate (X-ray + cosmic ray + radionuclide) with height in a protostellar disk. Based on the results of Igea & Glassgold (1999) and Aikawa & Herbst (1999a), we parameterise the total ionisation  as follows. Taking z0 as the height of the disk, the disk is divided vertically into three regions; the midplane,
as follows. Taking z0 as the height of the disk, the disk is divided vertically into three regions; the midplane,
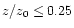 ;
the surface,
;
the surface,
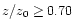 ;
and the intermediate. In the midplane region, the only significant ionisation process is radionuclides, so
;
and the intermediate. In the midplane region, the only significant ionisation process is radionuclides, so
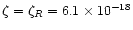 s-1. In the surface region, the total ionisation varies linearly between
s-1. In the surface region, the total ionisation varies linearly between
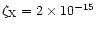 at R=10 AU and
at R=10 AU and
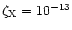 s-1 at R=1 AU. In the intermediate region, the ionisation varies linearly between
s-1 at R=1 AU. In the intermediate region, the ionisation varies linearly between 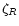 at
z/z0=0.25 to
at
z/z0=0.25 to
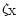 at z/z0=0.7. Results are presented for the cases with and without X-ray ionisation.
at z/z0=0.7. Results are presented for the cases with and without X-ray ionisation.
Adsorption and desorption mechanisms provide the gas-grain interaction in the model. The adsorption rate of a species x is given by
where Sx is the sticking coefficient for the freezing of species onto grains, a is the grain radius, 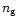 the grain number density, and vx and nx are the velocity and number density of the species x. We have taken Sx=0.3 for all neutral species. For ions, the coefficient is multiplied by a factor
the grain number density, and vx and nx are the velocity and number density of the species x. We have taken Sx=0.3 for all neutral species. For ions, the coefficient is multiplied by a factor
where a is the grain radius in cm and T is the grain temperature in K (Rawlings et al. 1992). The grain temperature is always taken to be the same as the gas temperature. The factor C takes into account the fact that grains are negatively charged (Umebayashi & Nakano 1981) and therefore the positively charged ions will be attracted to them more than neutral species.
Species can be desorbed from grain surfaces by thermal heating or cosmic ray heating. The latter process occurs when a cosmic ray particle deposits heat in a grain, so it will only be significant near the surface where cosmic rays can penetrate. The main desorption mechanism in the inner regions of the disk studied here is thermal desorption, simple evaporation. The process for calculating the rates of desorption is described in Hasegawa et al. (1992). This rate depends on the binding energy of the species, which are taken from that source, except in a few cases (see Willacy et al. 1998).
The chemical model was evaluated at each output point from the dynamical model, to build up a map of the molecular distributions. The grid of chemical calculations was therefore 10 cells in the radial direction and 100 cells vertically. The number of radial cells will be increased in future calculations. We started in the midplane at r=10 AU, and calculated vertically using the output from the previous step as input to the next - in this way the calculations were completed quite quickly. When determing the time for which to integrate each chemical model, we considered the viscous timescale and never integrated for longer than 10% of the timescale for radial transport (Willacy et al. 1998).
In Figs. 3-10, the results of this study are presented, for molecules detected in emission in DM Tau by Dutrey et al. (1997). The contour plots in Figs. 3, 4 and 6 show the logarithm of the fractional abundance of each species relative to total H nuclei. The colour postscript versions of these plots are available for download and printing at http://www.ajmarkwick.com/disks/.
The molecular distributions in the models with and without X-ray ionisation show large quantitative differences for ionic species, like HCO+, and also for some neutrals, like CN and C2H. For some species like H2CO, the difference is less marked.
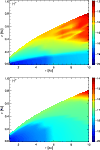 |
Figure 3:
Comparison of the molecular distributions of H+ in the disk, for the cases with (top) and without (bottom) the treatment of X-ray ionisation. The contours show the log fractional abundance of H+ relative to total H nuclei. These plots directly reflect the different ionisation structures in the two cases. |
| Open with DEXTER |
Generally, ions find their abundances greatest near the surface of the disk, seen for example in the plots of H+ (Fig. 3). In the case without X-rays, the ionisation fraction 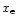 is in the range
is in the range
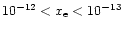 .
The dominant ion is either CH3CO+ near the midplane or HCO+ near the surface, as shown in Table 1. HCO+ is formed by the reaction of CO with H3+, and is the dominant ion in the colder regions (near the surface, further from the central object) because CO can remain in the gas in these regions where molecules needed to form other ions have already frozen out onto grains. In the warmer parts of the disk where most molecules are in the gas phase, the dominant ion changes to CH3CO+. This ion is formed by the radiative association of CH3+ and CO;
.
The dominant ion is either CH3CO+ near the midplane or HCO+ near the surface, as shown in Table 1. HCO+ is formed by the reaction of CO with H3+, and is the dominant ion in the colder regions (near the surface, further from the central object) because CO can remain in the gas in these regions where molecules needed to form other ions have already frozen out onto grains. In the warmer parts of the disk where most molecules are in the gas phase, the dominant ion changes to CH3CO+. This ion is formed by the radiative association of CH3+ and CO;
CH3+ is produced from methane, either directly by reaction with H+, or indirectly through the sequence
In the model with X-ray ionisation, the ionisation fraction 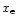 can reach 10-10. Table 1 shows that in the intermediate region, CH3CO+ is replaced as the dominant ion by HCNH+, an ion which is prevalent in the high ionisation model.
can reach 10-10. Table 1 shows that in the intermediate region, CH3CO+ is replaced as the dominant ion by HCNH+, an ion which is prevalent in the high ionisation model.
Table 1:
The dominant ion throughout the disk. The disk is split into bands of z/z0 between the surface (z/z0=1) and the midplane (z/z0=0).
Without X-rays:
| radius (AU) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| surface |
1 |
2 |
3 |
3 |
4 |
4 |
4 |
4 |
4 |
4 |
| 0.8 |
5 |
5 |
5 |
6 |
7 |
3 |
4 |
4 |
4 |
4 |
| 0.6 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
4 |
4 |
4 |
| 0.4 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
| 0.2 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
| midplane |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
With X-rays:
| radius (AU) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| surface |
4 |
1 |
4 |
4 |
8 |
8 |
8 |
8 |
8 |
8 |
| 0.8 |
9 |
9 |
9 |
1 |
1 |
8 |
8 |
8 |
8 |
8 |
| 0.6 |
1 |
1 |
9 |
4 |
1 |
1 |
8 |
8 |
8 |
8 |
| 0.4 |
9 |
1 |
1 |
9 |
4 |
1 |
1 |
4 |
4 |
8 |
| 0.2 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
4 |
| midplane |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
Key: 1 = HCNH+; 2 = H2C3N+; 3 = C3H4+; 4 = HCO+;
5 = CH3CO+; 6 = NH4+; 7 = C3H5+; 8 = H3+; 9 = H4C2N+.
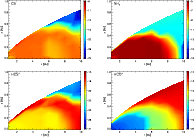 |
Figure 4:
The molecular distributions of CS, NH3, HCO+ and HCS+ in the disk (clockwise from top left). The contours show the log fractional abundance of H+ relative to total H nuclei. |
| Open with DEXTER |
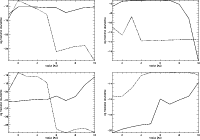 |
Figure 5:
The variation of log fractional abundance (relative to total H nuclei) of CS, NH3, HCO+ and HCS+ (clockwise from top left) with radius in the midplane (solid lines) and at the surface (dash lines) of the disk. |
| Open with DEXTER |
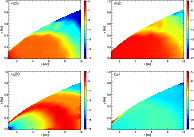 |
Figure 6:
As Fig. 4, but for HCN, HNC, C2H and H2CO (clockwise from top left). |
| Open with DEXTER |
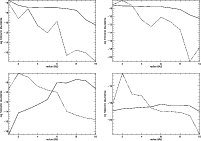 |
Figure 7:
As Fig. 5, but for HCN, HNC, C2H and H2CO (clockwise from top left). |
| Open with DEXTER |
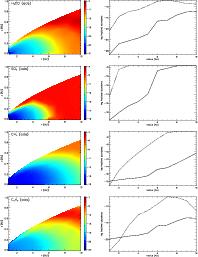 |
Figure 8:
The adsorbed abundance of H2CO, SO2, CH4 and C2H2 throughout the disk. The contours show the log fractional abundance of H+ relative to total H nuclei, and the panels on the right show the variation of the fractional abundances in the midplane (solid lines) and at the surface (dash lines) of the disk. |
| Open with DEXTER |
Most of the molecular distributions show some radial structure. The distribution of formaldehyde (H2CO), for example, has a ring-like form. In the midplane, its abundance seems to peak at around 8 AU. This can be understood by comparing the distribution of gaseous formaldehyde with that of its adsorbed counterpart. The ring structure in the gas phase distribution originates from the desorption of the molecule from grain surfaces. In the region 10 AU <R<8 AU, the adsorption drops by four orders of magnitude (Fig. 8), signifying the desorption of this species. Over the same region, the gas phase abundance increases (Fig. 6).
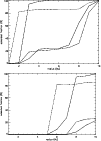 |
Figure 9:
The radial variation of the adsorbed fractions of the elements C (solid), N (dot), O (dash) and S (dash-dot) at the surface of the disk (top) and in the midplane (bottom). |
| Open with DEXTER |
The amount of adsorbed material follows the temperature profile of the disk. The composition of the mantles changes with temperature as well, as seen from Table 2 for R=10 AU. In the midplane, the ice mantle is mainly water, ammonia, CO and methane, while at the surface, the water ice fraction is less and there are more carbonaceous species adsorbed. Figure 9 shows the adsorbed fractions of each of the elements C, N, O and S at the surface and in the midplane of the disk. We see that at the surface, most material is in solid form at R=10 AU. Because observations tell us that there are molecules in the gas at radii much greater than this, there must be some desorption mechanisms at work there. Willacy et al. (1998) considered two mechanisms; cosmic ray heating and grain mantle explosions. However, they found that neither of these processes is efficient at maintaining significant gas phase abundances at radii greater than 10 AU, although the latter process is the more efficient of the two. In the model of Aikawa & Herbst (1999a), which is specifically concerned with the outer regions of the disk, up to 1000 AU, they achieve good agreement with observations by lowering the sticking probability from the normal value of 0.3 to 0.03. This simulates the effects of non-thermal desorption by restricting the amount of adsorption which can occur. Aikawa & Herbst use this result as evidence that some non-thermal desorption mechanism is operating in the outer disk, but do not speculate what it may be.
In this paper, we note that there is still quite a lot of material in the gas phase at the midplane (Fig. 9: bottom). This is especially true for carbon and nitrogen, which are only frozen out to around the 25% level at 10 AU. In the next section, we will see that this allows some molecules to persist in observable quantities.
Table 2:
The mantle composition in the disk at R=10 AU. The gas temperature here is 26.7 K (surface), 56.9 K (midplane).
| Species |
% (s) |
% (m) |
| H2O |
64.8 |
91.9 |
| CH4 |
14.3 |
1.9 |
| CO |
10.8 |
2.1 |
| N2 |
3.3 |
- |
| NH3 |
2.3 |
3.3 |
| CO2 |
1.4 |
- |
| C3H4 |
1.3 |
- |
| HCN |
0.4 |
- |
| HC3N |
0.1 |
0.2 |
| Other |
1.3 |
0.6 |
Table 3:
The top 30 highest vertical column densities in the model without X-ray ionisation, at radii 1, 5 and 10 AU from the central object.
| |
R=1 AU |
R=5 AU |
R=10 AU |
| |
Species |
log N (cm-2) |
Species |
log N (cm-2) |
Species |
log N (cm-2) |
| 1 |
He |
25.2 |
He |
24.8 |
He |
24.7 |
| 2 |
H2O |
22.2 |
H2O |
21.5 |
CH4 |
21.0 |
| 3 |
CH4 |
21.5 |
CH4 |
21.1 |
CO |
21.0 |
| 4 |
CO |
21.5 |
CO |
21.0 |
H |
20.6 |
| 5 |
H |
21.0 |
H |
20.9 |
N2 |
20.4 |
| 6 |
N2 |
21.0 |
N2 |
20.6 |
NO |
19.4 |
| 7 |
HCN |
20.4 |
NH3 |
20.2 |
O2 |
19.2 |
| 8 |
C3H4 |
20.4 |
CO2 |
20.1 |
HCN |
17.7 |
| 9 |
C4H2 |
20.0 |
C3H4 |
20.0 |
HNC |
17.7 |
| 10 |
NH3 |
20.0 |
C4H2 |
19.5 |
CH3CN |
17.2 |
| 11 |
HC3N |
20.0 |
C3H3 |
19.5 |
O |
17.1 |
| 12 |
C2H2 |
19.3 |
O2 |
18.9 |
C3H4 |
16.9 |
| 13 |
CH3CN |
19.3 |
HC3N |
18.9 |
C3H3 |
16.7 |
| 14 |
CO2 |
18.9 |
CH3CN |
18.9 |
H2CO |
16.6 |
| 15 |
HNC |
18.7 |
C2H2 |
18.8 |
C2H2 |
15.7 |
| 16 |
CH3OH |
18.5 |
NH2 |
18.7 |
H2CS |
15.0 |
| 17 |
CH3 |
18.4 |
HCN |
18.6 |
N |
15.0 |
| 18 |
O2 |
18.4 |
HNC |
18.1 |
CS |
14.6 |
| 19 |
SO2 |
18.3 |
CH3OH |
17.9 |
CH2CO |
14.6 |
| 20 |
CH2CO |
18.3 |
CH2CO |
17.9 |
SO |
13.5 |
| 21 |
SiH4 |
18.2 |
SO2 |
17.8 |
C2S |
13.1 |
| 22 |
Fe |
18.0 |
SiH4 |
17.6 |
C3H2 |
13.1 |
| 23 |
Mg |
18.0 |
Fe |
17.4 |
CN |
12.9 |
| 24 |
SiO |
17.7 |
C3H2 |
17.4 |
CH3 |
12.4 |
| 25 |
C3H3 |
17.5 |
SiO |
17.2 |
OH |
12.3 |
| 26 |
C3N |
17.3 |
CH3 |
17.2 |
HCO+ |
12.3 |
| 27 |
SiO2 |
17.3 |
H2CO |
17.1 |
NH2 |
11.6 |
| 28 |
C2H |
17.2 |
Mg |
17.0 |
CO2 |
11.5 |
| 29 |
O |
17.0 |
NO |
16.7 |
CH3CO+ |
11.3 |
| 30 |
C4H |
17.0 |
SiO2 |
16.5 |
HCS |
11.3 |
Table 4:
As Table 3, but for the model including X-ray ionisation.
| |
R=1 AU |
R=5 AU |
R=10 AU |
| |
Species |
log N (cm-2) |
Species |
log N (cm-2) |
Species |
log N (cm-2) |
| 1 |
He |
25.2 |
He |
24.8 |
He |
24.7 |
| 2 |
H2O |
22.2 |
H |
21.9 |
H |
22.3 |
| 3 |
CH4 |
21.5 |
H2O |
21.5 |
CH4 |
20.8 |
| 4 |
CO |
21.5 |
CH4 |
21.0 |
CO |
20.8 |
| 5 |
H |
21.4 |
CO |
21.0 |
N2 |
20.4 |
| 6 |
N2 |
21.0 |
N2 |
20.6 |
NO |
19.2 |
| 7 |
HCN |
20.3 |
CO2 |
20.1 |
O2 |
19.2 |
| 8 |
C3H4 |
20.3 |
C3H4 |
19.9 |
HCN |
17.9 |
| 9 |
C4H2 |
20.1 |
NH3 |
19.8 |
N |
17.9 |
| 10 |
NH3 |
19.9 |
C4H2 |
19.8 |
HNC |
17.8 |
| 11 |
HC3N |
19.9 |
C3H3 |
19.5 |
O |
17.6 |
| 12 |
C2H2 |
19.7 |
HC3N |
19.4 |
CH3 |
17.5 |
| 13 |
HNC |
19.6 |
CH3CN |
19.2 |
CH3CN |
17.2 |
| 14 |
CH3CN |
19.4 |
C2H2 |
19.0 |
C3H4 |
16.9 |
| 15 |
CO2 |
18.9 |
O2 |
19.0 |
C3H3 |
16.8 |
| 16 |
CH3 |
18.8 |
HCN |
18.6 |
H2CO |
16.6 |
| 17 |
C3H3 |
18.8 |
CH3OH |
18.3 |
C2H2 |
15.8 |
| 18 |
C3H |
18.7 |
HNC |
18.3 |
NH2 |
15.4 |
| 19 |
CH3OH |
18.5 |
SO2 |
17.8 |
H2CS |
15.0 |
| 20 |
O2 |
18.3 |
SiH4 |
17.6 |
CS |
14.6 |
| 21 |
SO2 |
18.3 |
NH2 |
17.6 |
CH2CO |
14.6 |
| 22 |
CH2CO |
18.2 |
CH2CO |
17.5 |
CN |
14.6 |
| 23 |
SiH4 |
18.2 |
C3H2 |
17.5 |
OH |
14.4 |
| 24 |
C3N |
18.1 |
Fe |
17.4 |
C |
14.4 |
| 25 |
Fe |
18.0 |
H2CO |
17.4 |
HCO+ |
14.1 |
| 26 |
Mg |
18.0 |
C3N |
17.3 |
NH |
13.7 |
| 27 |
SiO |
17.7 |
SiO2 |
17.0 |
SO |
13.6 |
| 28 |
SiO2 |
17.2 |
SiO |
17.0 |
HCNH+ |
13.2 |
| 29 |
H2CS |
16.8 |
Mg |
17.0 |
C2S |
13.1 |
| 30 |
C4H |
16.8 |
O |
16.9 |
N2H+ |
13.1 |
The radial distributions of vertical column densities for some molecules are shown in Fig. 10. Tables 3 and 4 list the atomic and molecular species with the highest vertical column densities at radii of 1, 5 and 10 AU, for the low and high ionisation models respectively. The column density of species X is calculated from its number density of n(X), using the formula
which is evaluated over the disk height using numerical quadrature from the calculated abundances. The 5-point Newton-Cotes formula was used. A comparison with observations would be desirable, but unfortunately observational data for a region so close to the central object are as yet unavailable. The observations of DM Tau by Dutrey et al. (1997) were only sensitive to the outer regions of the disk, and further, their data were interpreted on the basis of the relative abundances remaining constant throughout the disk. Hopefully, data will be available in the near future so that a comparison can be made.
From Tables 3 and 4 we see that there are some molecules whose column densities at 10 AU are appreciable. These include the species already discussed, such as HCN, HNC, CH4 and H2CO, but also molecules such as methyl acetylene (propyne; CH3CCH), methyl cyanide (CH3CN), acetylene (C2H2) and ketene (CH2CO). The presence of such molecules in large quantities in the gas phase at radii 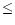 10 AU is interesting because we are describing the chemical state of the gas out of which planets form, and these species are the chemical building blocks of more complex organic compounds.
10 AU is interesting because we are describing the chemical state of the gas out of which planets form, and these species are the chemical building blocks of more complex organic compounds.
It is clear that the level of ionisation makes a large difference to the column density of some species, and as such, observations of C2H or CN for example, would be useful in measuring the actual effect of such processes on the chemistry in protostellar disks. Figure 10 shows that the column density of the cyanogen radical CN changes by over 4 orders of magnitude depending on the ionisation level. The two models are identical except for the ionisation profile and so all differences must be traceable back to this. In the case of CN, the analysis is quite straightforward. Nine of the top ten formation reactions are ion-neutral or dissociative recombination, involving ions like C+, He+, H2C3N+, HCNH+, etc., independent of the ionisation level. When the ionisation is low, the main formations are those with C+ and He+, but as these molecules are relatively unabundant, the formation of CN is very inefficient. Because the formation of CN is dependent on ion-neutral chemistry, it suffers when ions are not abundant. Worse for CN, it is destroyed by neutral-neutral reactions, like its reaction with acetylene which makes HC3N, or its reaction with ammonia which produces hydrogen cyanide. CN is also a photodissociation product of HCN. We find that in regions of low ionisation, CN is destroyed 100 times faster than it is formed. Hence, it is quite unabundant in the low ionisation model.
The ethynyl radical, C2H, also shows a marked increase in column density when 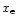 is high. This is true of the whole family of polyyne molecules CnH. The reason for this is because they are mainly formed by dissociative recombination of hydrocarbon ions;
is high. This is true of the whole family of polyyne molecules CnH. The reason for this is because they are mainly formed by dissociative recombination of hydrocarbon ions;
The hydrocarbon ions, CnH2+ are ultimately formed by ion-neutral reactions between gas phase ions and neutral species desorbed from grain surfaces. C2H is a photodissociation product of C2H2. When the ionisation level is low, these processes will be less efficient.
On the other hand, formaldehyde, H2CO, shows almost no change in its vertical column density between the ionisation models (see Fig. 10). As previously noted, in this model the formation of H2CO is principally due to its desorption from grains. Subsequently, the molecule is retained by the following cycle of proton transfer and recombination;
If 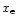 is high, the cycle goes quickly, and if xe is low, the cycle hardly goes at all, but H2CO persists because all the main destruction routes are ion-neutral reactions. This is borne out by the observation that in both models, the formation and destruction rates of H2CO are nearly the same.
is high, the cycle goes quickly, and if xe is low, the cycle hardly goes at all, but H2CO persists because all the main destruction routes are ion-neutral reactions. This is borne out by the observation that in both models, the formation and destruction rates of H2CO are nearly the same.
A protostellar disk is an interesting place for comparing ion-neutral chemistry with that of neutral-neutral chemistry. As one moves from the midplane of the disk upward, the ionisation level increases. In the studied case with X-ray ionisation, this change is quite drastic and there is the opportunity to examine both kinds of chemistry in the same object at the same time.
A comparison of our results with the results obtained in the previous studies described in the introduction is difficult since the models discussed all differ either in their physical basis (i.e. which disk model is used), in their chemical details (whether gas-grain interaction is included, for example) or both. Therefore we are forced to make global statements about the differences in the models. Compared to the midplane model of Willacy et al. (1998), our results are similar. We expect this because the chemical model is similar. Compared to the midplane model of Finocchi & Gail (1997; FG97), the results differ more greatly, but this is associated with the model details, specifically that we have included desorption of species from grain mantles, and FG97 include grain sputtering and destruction. In each case, the temperature profile dictates where these two processes will become significant in the disk, and in the two models this profile is different. Taking ammonia as an example, in the low ionisation model presented here, at 1 AU the fractional abundance is
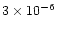 (relative to total H nuclei). In the model of FG97 the value is
(relative to total H nuclei). In the model of FG97 the value is
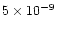 .
This large discrepancy is due to the desorption of NH3 from grain mantles, which occurs in our model. In the case of methane, FG97 showed that its abundance changes dramatically as one approaches a radius of 1 AU, where it has increased from a negligible fractional abundance at 5 AU to
.
This large discrepancy is due to the desorption of NH3 from grain mantles, which occurs in our model. In the case of methane, FG97 showed that its abundance changes dramatically as one approaches a radius of 1 AU, where it has increased from a negligible fractional abundance at 5 AU to
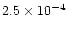 .
In our model the abundance at 1 AU is
.
In our model the abundance at 1 AU is
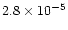 ,
but it is
,
but it is
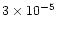 at 5 AU. Therefore in our model methane is already present in a large quantity at 5 AU due to its desorption from grains, which can be seen in Fig. 8 and in Table 3. It is being chemically processed away by the time we reach 1 AU. This trend is present in many of the molecules which are primarily desorbed from grains in our model, e.g. H2CO, SO2.
at 5 AU. Therefore in our model methane is already present in a large quantity at 5 AU due to its desorption from grains, which can be seen in Fig. 8 and in Table 3. It is being chemically processed away by the time we reach 1 AU. This trend is present in many of the molecules which are primarily desorbed from grains in our model, e.g. H2CO, SO2.
Comparing our model with the previously published (R,z) models is also difficult because they all focus on radii >100 AU, whereas we are interested in the inner regions where R<10 AU. It is possible however to compare the column densities derived for large radii with ours at small radii, and this is done in Table 5. Once again the main differences are produced by desorption of mantle species. The column density of CO increases by orders of magnitude in the inner regions of the disk. At 50 AU in the model of Willacy & Langer (2000) the column density is 1019 cm-2, intermediate between the values at 100 AU and 5 AU (see also Fig. 10). This is consistent with the radius of desorption of mantle carbon monoxide, and also applies to the other species which are largely affected by grain mantle desorption, for example HCN, H2CO and NH3.
The ethynyl radical C2H has a lower column density in the inner regions of the disk than in the outer. This can be explained because the other models have included photoprocesses in the regions away from the midplane. Indeed, taking the value from our model with X-ray ionisation, we get a column density of 1015 cm-2 at 5 AU. In that case, the comparison is completely different, but is consistent with the discussion of the differences between the model with and without X-ray ionisation and our identification of C2H as a good tracer of the ionisation level in the disk. The same argument applies to CN and HCO+, which also appear to decrease in Table 5.
It is also worth noting that the values derived between the two models at 100 and 300 AU do not agree in some cases, especially CO, HCO+ and H2CO. The major difference between these two models is the physical model for the disk parameters. Willacy & Langer (2000) use the model of Chiang & Goldreich (1997) while Aikawa & Herbst (1999a) use a model based on the minimum mass solar nebula. The significant difference in terms of an (R,z) chemistry is that the former has a vertical temperature profile, whereas the latter is isothermal in the z-direction. This only serves to confirm our conclusion that the temperature profile is a critical ingredient for chemical modelling of protostellar disks.
Table 5:
Comparison of our model results at 1 AU (low ionisation) with those of previous (R,z) models at 100 and 300 AU. The tabulated values are log column densities (cm-2). References: Willacy & Langer 2000 (first block); Aikawa & Herbst 1999a (second block).
| Species |
5 AU |
100 AU |
300 AU |
100 AU |
300 AU |
| CO |
21.0 |
16.9 |
16.9 |
19.8 |
16.5 |
| CS |
15.4 |
9.5 |
11.0 |
11.9 |
12.5 |
| NH3 |
20.3 |
- |
- |
14.1 |
15.0 |
| HCO+ |
11.5 |
10.9 |
10.7 |
13.3 |
12.0 |
| HCN |
18.7 |
12.5 |
12.1 |
13.2 |
13.5 |
| C2H |
9.6 |
10.6 |
12.0 |
12.1 |
12.5 |
| H2CO |
17.0 |
10.8 |
10.7 |
12.6 |
12.2 |
| CN |
11.7 |
11.3 |
11.6 |
12.6 |
13.0 |
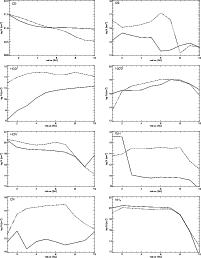 |
Figure 10:
The radial distribution of column densities for the molecules CO, CS, HCO+, H2CO, HCN, C2H, CN and NH3 in the disk. The dashed line shows the X-ray ionisation model. |
| Open with DEXTER |
We have presented distributions of molecules in the inner regions of a protostellar disk. They were calculated from a one point chemical model using a numerical integration to get the vertical disk structure.
In the inner regions studied here, thermal desorption dominates the chemistry. The temperature profile also determines the radius at which dust destruction occurs. In our model, no dust is destroyed outside a radius of 1 AU. Because of these facts, the temperature profile adopted or the method used to calculate it is extremely significant in modelling the molecular distributions.
We performed our calculations with and without a treatment of X-ray ionisation, and found that certain species are good tracers of the ionisation level in the disk, especially CN and C2H, whose column densities vary widely between the two cases. This is in agreement with other studies (e.g. Aikawa & Herbst 2001), and suggests that further observations of these molecules will be useful in determining the ionisation structure of protostellar disks. The column density of other species (e.g. H2CO) is less dependent on the ionisation, but is sensitive to the level of thermal desorption occurring, and so could be used to trace the temperature in these inner regions of protostellar disks.
Although gas phase material freezes out onto dust grains as one moves outward in the disk, we have shown that there is still an appreciable column density in certain molecules at 10 AU, including some organic species, which would be good candidates for future observational studies.
Finally, dynamical effects which couple directly to the chemistry, such as diffusion, have not been incorporated in this model, and have not been studied in this context by other authors. The effects of these processes on the chemistry in protostellar disks will be the subject of a forthcoming paper (Ilgner et al. 2002, in preparation).
Acknowledgements
Research in Astrophysics at UMIST is supported by PPARC. The Jena group is supported by DFG grant He 1935/5-3.
-
Aikawa, Y., & Herbst, E. 1999a, A&A, 351, 233
In the text
NASA ADS
-
Aikawa, Y., & Herbst, E. 1999b, ApJ, 526, 314
NASA ADS
-
Aikawa, Y., & Herbst, E. 2001, A&A, 371, 1107
In the text
NASA ADS
-
Aikawa, Y., Miyama, S. M., Nakano, T., & Umebayashi, T. 1996, ApJ, 467, 684
In the text
NASA ADS
-
Aikawa, Y., Umebayashi, T., Nakano, T., & Miyama, S. M. 1999, ApJ, 519, 705
In the text
NASA ADS
-
Bauer, I., Finocchi, F., Duschl, W. J., Gail, H.-P., & Schlöder, J. P. 1997, A&A, 317, 273
In the text
NASA ADS
-
Bell, K. R., Cassen, P. M., Klahr, H. H., & Henning, Th. 1997, ApJ, 486, 372
In the text
NASA ADS
-
Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368
In the text
NASA ADS
-
D'Alessio, P., Canto, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411
NASA ADS
-
Dutrey, A., Guilloteau, S., & Guelin, M. 1997, A&A, 317, 55
In the text
-
Finocchi, F., & Gail, H.-P. 1997, A&A, 327, 825
NASA ADS
-
Finocchi, F., Gail, H.-P., & Duschl, W. J. 1997, A&A, 325, 1264
In the text
NASA ADS
-
Gail, H.-P. 1998, A&A, 332, 1099
In the text
NASA ADS
-
Glassgold, A. E., Najita, J., & Igea, J. 1997, ApJ, 480, 344
In the text
NASA ADS
-
Guilloteau, S., & Dutrey, A. 1994, A&A, 291, 23
In the text
-
Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167
In the text
NASA ADS
-
Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35
In the text
NASA ADS
-
Igea, J., & Glassgold, A. E. 1999, ApJ, 518, 848
In the text
NASA ADS
-
Kippenhahn, R., & Weigert, A. 1994, Stellar Structure and Evolution (Springer, Berlin)
In the text
-
Lee, T., Papanastassiou, D. A., & Wasserburg, G. J. 1977, Geochimica et Cosmochimica Acta, 41, 1473
In the text
NASA ADS
-
Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321
In the text
NASA ADS
-
Lin, D. N. C., & Papaloizou, J. C. B., in Protostar and Planets II, ed. D. C. Black, & M. S. Mathews (University of Arizona, Tucson), 981
-
Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603
In the text
NASA ADS
-
Mahoney, W. A., Ling, J. C., Wheaton, W. A., & Jacobson, A. S. 1984, ApJ, 286, 578
In the text
NASA ADS
-
Meyer, F., & Meyer-Hofmeister, E. 1982, A&A, 106, 34
In the text
NASA ADS
-
Qi, C. 2000, Ph.D. Thesis, Pasadena, California
In the text
-
Rawlings, J. M. C., Hartquist, T. W., Menten, K. M., & Williams, D. A. 1992, MNRAS, 255, 471
In the text
NASA ADS
-
Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337
In the text
NASA ADS
-
Umebayashi, U., & Nakano, T. 1981, PASJ, 33, 617
In the text
NASA ADS
-
Willacy, K. A., Klahr, H. H., Millar, T. J., & Henning, Th. 1998, A&A, 338, 995
In the text
NASA ADS
-
Willacy, K. A., & Langer, W. D. 2000, ApJ, 544, 903
In the text
NASA ADS
Copyright ESO 2002

![\begin{displaymath}\sigma T_{{\rm acc}}^4 = \frac{3}{8 \pi}
\frac{\gamma M_{\as...
...}}{r_{}^3} \left[ 1-\beta \sqrt{\frac{R_{\ast}^{}}{r}}\right],
\end{displaymath}](/articles/aa/full/2002/14/aa1884/img17.gif)