Appendix B: Notes on the numerical computations

The computations have been carried out analytically as far as possible and we have used the software Mathematica (Wolfram 1999). However, some of the results have been obtained numerically.

• The residual intensity 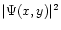$\vert\Psi(x,y)\vert^2$ (computed with Eq. (10)) cannot be integrated analytically to obtain the residual star energy, and the integration must be performed numerically. We have used a Gauss-Kronrod integration algorithm provided by Mathematica.
• The optimal parameters a and b have been obtained with a numerical minimization of the residual energy criterion, using a conjugate gradient method.

• The Fourier transform to compute the final residual intensities for the star can be separated into a difference of one-dimensional computations. If we consider the spatial limitation of the Lyot's stop and the symmetry properties of the residual wave amplitude, the Fourier integral can be favorably computed directly within the finite exit pupil, with only the cosine terms and using a numerical integration algorithm.

Acknowledgements

The authors would like to thank François Martin for his very helpful contribution to the preliminary laboratory tests of the interferometric apodization technique. Thanks are also due to François-Xavier Schmider for interesting discussions.