A&A 379, 305-322 (2001)
DOI: 10.1051/0004-6361:20011261
R. Alvarez1
- A. Jorissen1,![]() - B. Plez2 - D. Gillet3 - A. Fokin4 - M. Dedecker1,
- B. Plez2 - D. Gillet3 - A. Fokin4 - M. Dedecker1,![]()
1 - Institut d'Astronomie et d'Astrophysique,
Université Libre de Bruxelles,
CP226, Boulevard du Triomphe,
1050 Bruxelles, Belgium
2 -
GRAAL,
Université Montpellier II,
cc072,
34095 Montpellier Cedex 05, France
3 -
Observatoire de Haute-Provence,
04870 Saint-Michel l'Observatoire, France
4 -
Institute for Astronomy of the Russia Academy of Sciences,
48 Pjatnitskaja,
109017 Moscow, Russia
Received 30 March 2001 / Accepted 22 August 2001
Abstract
This paper presents statistics of the line-doubling phenomenon in a sample of
81 long-period variable (LPV) stars of various periods, spectral types and
brightness ranges. The set of observations consists of 315
high-resolution optical spectra collected with the spectrograph ELODIE at the
Haute-Provence Observatory, during 27 observing nights at one-month intervals and
spanning two years.
When correlated with a mask mimicking a K0III spectrum, 54% of the sample stars
clearly showed a double-peaked cross-correlation profile around maximum light,
reflecting double absorption lines.
Several pieces of evidence are presented that point towards the double absorption
lines as being caused by the propagation of a shock wave through the photosphere.
The observation of the Balmer lines appearing in emission
around maximum light in these stars
corroborates the presence of a shock wave.
The observed velocity discontinuities, ranging between 10 and
25 km s-1, are not correlated with the brightness ranges.
A comparison with the center-of-mass (COM) velocity obtained
from submm CO lines originating in the circumstellar envelope reveals that the
median velocity between the red and blue peaks is blueshifted with respect to
the COM velocity, as expected if the shock moves upwards.
The LPVs
clearly exhibiting line-doubling around maximum light with the K0III mask
appear to be the
most compact ones, the stellar radius being
estimated from their effective temperatures (via the
spectral
type) and luminosities (via the period-luminosity relationship).
It is not entirely clear whether or not this segregation between
compact and extended LPVs is an
artefact of the use of the K0III
mask. Warmer masks (F0V and G2V) applied to the most extended
and coolest LPVs yield asymmetric
cross-correlation functions which suggest that line doubling is
occurring in those stars as well. Although a firm conclusion on this
point is hampered by the large correlation noise present in the
CCFs of cool LPVs obtained with warm masks, the occurrence of line
doubling in those stars is confirmed by the double
CO
![]() lines observed around 1.6
lines observed around 1.6 ![]() m by Hinkle
et al. (1984, ApJS, 56, 1).
Moreover, the H
m by Hinkle
et al. (1984, ApJS, 56, 1).
Moreover, the H![]() line in emission, which is another signature of the
presence of shocks, is observed as well
in the most extended stars,
although with a
somewhat narrower profile. This is an indication that the shock is
weaker in extended than in compact LPVs, which may also contribute to
the difficulty of detecting line doubling in cool, extended LPVs.
line in emission, which is another signature of the
presence of shocks, is observed as well
in the most extended stars,
although with a
somewhat narrower profile. This is an indication that the shock is
weaker in extended than in compact LPVs, which may also contribute to
the difficulty of detecting line doubling in cool, extended LPVs.
Key words: stars: AGB and post-AGB - stars: atmospheres - stars: late-type - stars: oscillations - stars: variables: general - shock waves
Long-period variable stars (LPVs) are cool giant stars of low and intermediate masses, and the light variations associated with the pulsation of their envelope have long periods (typically 300 d) and large amplitudes (up to 9 magnitudes peak-to-peak in the visual). LPVs are subdivided into Mira Ceti-type variables (Mira stars or Miras) and semi-regular variables (of the SRa or SRb subtypes), depending on the light curve amplitude, shape and regularity.
Apart from the brightness fluctuations, LPVs are characterized by striking spectral changes:
Merrill (1955) was the first to suggest that the spectral changes observed in LPVs may be explained by the presence of a shock wave moving outward. This idea has been extensively investigated since then by a number of authors: e.g. Gorbatskii (1957, 1961), Willson (1972, 1976), Hinkle (1978), Willson & Hill (1979), Hill & Willson (1979), Wood (1979), Willson et al. (1982), Gillet & Lafon (1983, 1984, 1990), Fox et al. (1984), Fox & Wood (1985), Bessell et al. (1996), Fadeyev & Gillet (2000, 2001).
Nevertheless, due to the lack of a complete and self-consistent model describing the pulsation and its effect on the spectrum, most of the questions raised by the spectral peculiarities of LPVs remain unanswered so far. For instance, the origin of the emission lines is still debated: although most authors believe they are formed in the hot wake of the shock (Gillet 1988a; de la Reza 1986 and references therein), others reject the shock wave scenario and invoke instead purely non-LTE radiative processes (Magnan & de Laverny 1997).
The velocity of the shock front is also a matter of debate: large shock-wave velocity discontinuities (of the order of 60 km s-1) are indeed required to photodissociate H2 molecules and photoionize hydrogen atoms in order to subsequently produce by recombination the observed Balmer emission lines (Gillet et al. 1989). Velocity discontinuities of that order are indeed observed for fluorescent lines (Willson 1976), although double absorption lines yield much lower velocity discontinuities (of the order of 20-30 km s-1; e.g. Adams 1941; Merrill & Greenstein 1958; Maehara 1968; Tsuji 1971; Hinkle 1978; Hill & Willson 1979; Hinkle et al. 1997 and references therein). The lower velocity discontinuities derived from absorption lines are not necessarily incompatible with the theoretical requirement, since the velocities of the blue and red components suffer from a strong averaging effect due to the large extension of the region where they form.
The line-doubling phenomenon is source of conflicting theories. Some important progress towards its understanding has however been made recently thanks to a dedicated monitoring of Mira variables (Alvarez et al. 2000a, hereafter 1), which confirmed that the line-doubling phenomenon is caused by a shock wave propagating in the photosphere. It was shown that the temporal evolution of the red and blue peaks of the double absorption lines of the Mira variable RTCyg is consistent with the so-called "Schwarzschild scenario''. This scenario, originally presented by Schwarzschild (1952) for WVir Cepheids, relates the evolution of the line profile to the progression of a shock wave in the atmosphere. Alternative models accounting for line doubling without resorting to differential atmospheric motions (Karp 1975; Gillet et al. 1985a) can thus be definitively rejected.
It was shown in 1 that some LPVs (e.g., XOph) do not (or, at least, not clearly) exhibit line doubling around maximum light. This paper further investigates the questions raised by this result: what is the frequency of Mira variables exhibiting line-doubling around maximum light (Sect. 4.3.1) and what are their distinctive properties (Sect. 4)? To address these questions, a large sample of LPVs (mostly Mira variables) of various spectral types was monitored during 2 years (Sect. 2).
This section describes the two-year-long monitoring of a large sample of LPV stars performed with ELODIE at the Observatoire de Haute-Provence (France) at a frequency of about one night per month, weather-permitting.
The fibre-fed echelle spectrograph ELODIE (Baranne et al. 1996) is mounted
on the 1.93-m telescope of the Observatoire de Haute-Provence (France). This
instrument is designed to perform very accurate radial-velocity measurements
by cross-correlating the stellar spectrum with numerical masks. In one
exposure an echelle spectrum at a resolution of 42000 ranging from
3906 Å to 6811 Å is recorded. Then, an automatic on-line data
processing extracts a 2-D spectrum (67 orders ![]() 1044 pixels) from the
echelle spectrum. We developed our own cross-correlation procedure, following
the prescriptions of Baranne et al. (1996). We have thus the possibility
of using our own numerical templates and to perform different kinds of tests in
the computation of the cross-correlation function (CCF). The CCF is computed
directly from the 2-D spectrum. First, it is wavelength-calibrated, then
corrected from the value of the Earth barycentric velocity towards the star.
To preserve the accuracy, the CCF is computed without either rebinning or
merging the orders. Only orders having an average signal-to-noise
(S/N) ratio
greater than 2.0 are used.
1044 pixels) from the
echelle spectrum. We developed our own cross-correlation procedure, following
the prescriptions of Baranne et al. (1996). We have thus the possibility
of using our own numerical templates and to perform different kinds of tests in
the computation of the cross-correlation function (CCF). The CCF is computed
directly from the 2-D spectrum. First, it is wavelength-calibrated, then
corrected from the value of the Earth barycentric velocity towards the star.
To preserve the accuracy, the CCF is computed without either rebinning or
merging the orders. Only orders having an average signal-to-noise
(S/N) ratio
greater than 2.0 are used.
Two templates have been systematically used in a first step to compute the CCFs of the whole sample: (i) the default K0III mask provided in the ELODIE reduction software (Baranne et al. 1996); (ii) a M4V mask constructed by Delfosse et al. (1999) from an ELODIE spectrum of Barnard's star (Gl 699) applying the method of Baranne et al. (1979). Although the K0III template may in fact seem inadequate to study much cooler LPVs, it was argued in Sect. 2.2 of Alvarez et al. (2001; hereafter Paper II) that "warm'' masks like the K0III one are more prone to detect line doubling (see also Sects. 3 and 4.3.2.1). On the other hand, it has been checked a posteriori (see the discussion in Sect. 4.3.2.1 in relation with Fig. 10) that the M4V mask yields CCFs that are identical to those obtained with a mask mimicking the spectrum of the M4.5III star HD 123657 (see Table 1).
The sample is composed of: (i) 6 circumpolar Miras (SUCam, SUMi, RTDra, AXCep, SCep, RYCep) that can be observed all along the pulsational cycle; (ii) 76 LPVs (Mira and semi-regular variables) of different periods, chemical compositions, spectral types and brightness ranges, observed at different phases; (iii) 8 non-LPV red giants; (iv) 3 radial-velocity standard stars. The entire sample (93 stars) is presented in Table 1: for each star are indicated its GCVS (General Catalogue of Variable Stars, Kholopov et al. 1988) name (or the HD number); its right ascension and declination (2000.0); its variability type, period, spectral type and brightness range as given by the GCVS; the number of observations N. The last column indicates whether the star is circumpolar ("circum.''), non-LPV ("non-LPV'') or radial-velocity standard ("r.v. st.'').
| Name | Right Asc. | Declination | Variability | Period | Spectral | Brightness | N | Comments |
| (2000.0) | (2000.0) | Type | (d) | Type | Range | |||
| SV And | 00:04:20 | +40:06:36 | Mira | 316.21 | M5e-M7e | 7.7-14.3 | 2 | |
| T And | 00:22:23 | +26:59:46 | Mira | 280.76 | M4e-M7.5e | 7.7-14.5 | 2 | |
| R And | 00:24:02 | +38:34:39 | Mira | 409.33 | S3,5e-S8,8e | 5.8-14.9 | 1 | |
| Y Cep | 00:38:22 | +80:21:24 | Mira | 332.57 | M5e-M8.2e | 8.1-16.0 | 1 | |
| U Psc | 01:22:58 | +12:41:54 | Mira | 173.10 | M4e | 10.3-14.9 | 1 | |
| R Psc | 01:30:38 | +02:52:55 | Mira | 344.50 | M3e-M6e | 7.0-14.8 | 5 | |
| Y And | 01:39:37 | +39:20:37 | Mira | 220.53 | M3e-M4.5e | 8.2-15.1 | 5 | |
| o Cet | 02:19:21 | -02:58:28 | Mira | 331.96 | M5e-M9e | 2.0-10.1 | 3 | |
| R Cet | 02:26:02 | -00:10:42 | Mira | 166.24 | M4e-M9 | 7.2-14.0 | 7 | |
| U Cet | 02:33:44 | -13:08:54 | Mira | 234.76 | M2e-M6e | 6.8-13.4 | 1 | |
| R Tri | 02:37:02 | +34:15:54 | Mira | 266.9 | M4IIIe-M8e | 5.4-12.6 | 3 | |
| U Ari | 03:11:03 | +14:47:58 | Mira | 371.13 | M4e-M9.5e | 7.2-15.2 | 5 | |
| SS Cep | 03:49:30 | +80:19:20 | SRb | 90.0 | M5III | 8.0- 9.1 | 3 | |
| R Tau | 04:28:18 | +10:09:44 | Mira | 320.90 | M5e-M9e | 7.6-15.8 | 4 | |
| V Tau | 04:52:02 | +17:32:18 | Mira | 168.7 | M0e-M4.5e | 8.5-14.6 | 4 | |
| R Aur | 05:17:18 | +53:35:11 | Mira | 457.51 | M6.5e-M9.5e | 6.7-13.9 | 3 | |
| W Aur | 05:26:55 | +36:54:11 | Mira | 274.27 | M3e-M8e | 8.0-15.3 | 2 | |
| RU Aur | 05:40:08 | +37:38:12 | Mira | 466.47 | M7e-M9e | 9.0-16.0 | 3 | |
| S Cam | 05:41:02 | +68:47:55 | SRa | 327.26 | C7,3e(R8e) | 7.7-11.6 | 5 | |
| 05:55:10 | +07:24:25 | SRc | M1 | 0.50 | 1 | non-LPV | ||
| U Ori | 05:55:49 | +20:10:31 | Mira | 368.3 | M6e-M9.5e | 4.8-13.0 | 4 | |
| 05:59:31 | +54:17:11 | K0 | 3.71 | 1 | non-LPV | |||
| X Aur | 06:12:13 | +50:13:41 | Mira | 162.79 | M3e-M7e | 8.0-13.6 | 2 | |
| 06:22:57 | +22:30:54 | Lb | M3 | 2.97 | 1 | non-LPV | ||
| SU Cam | 06:38:12 | +73:55:00 | Mira | 285.03 | M5 | 8.9-12.6 | 8 | circum. |
| X Gem | 06:47:07 | +30:16:35 | Mira | 264.16 | M5e-M8e(Tc:) | 7.5-13.8 | 3 | |
| X Mon | 06:57:12 | -09:03:51 | SRa | 155.80 | M1eIII-M6ep | 6.8-10.2 | 1 | |
| R Gem | 07:07:21 | +22:42:13 | Mira | 369.91 | S2.9e-S8.9e | 6.0-14.0 | 7 | |
| R CMi | 07:08:43 | +10:01:27 | Mira | 337.78 | C7,1Je(CSep) | 7.25-11.6 | 1 | |
| S CMi | 07:32:43 | +08:19:07 | Mira | 332.94 | M6e-M8e | 6.6-13.2 | 5 | |
| 07:35:55 | +26:53:50 | M0 | 4.06 | 1 | non-LPV | |||
| 81 Gem | 07:46:08 | +18:30:39 | K4 | 4.87 | 1 | non-LPV | ||
| R Cnc | 08:16:34 | +11:43:35 | Mira | 361.6 | M6e-M9e | 6.07-11.8 | 5 | |
| X UMa | 08:40:49 | +50:08:11 | Mira | 249.04 | M3e-M4e | 8.1-14.8 | 4 | |
| HD 76830 | 08:59:11 | +18:08:09 | M4 | 6.38 | 1 | non-LPV | ||
| UZ Hya | 09:16:45 | -04:36:24 | Mira | 260.95 | M4e | 8.8-14.5 | 5 | |
| R Leo | 09:47:33 | +11:25:46 | Mira | 309.95 | M6e-M8IIIe | 4.4-11.3 | 3 | |
| S LMi | 09:53:43 | +34:55:32 | Mira | 233.83 | M2.0e-M8.2e | 7.5-14.3 | 2 | |
| V Leo | 10:00:02 | +21:15:40 | Mira | 273.35 | M5e | 8.4-14.6 | 4 | |
| R UMa | 10:44:39 | +68:46:33 | Mira | 301.62 | M3e-M9e | 6.5-13.7 | 4 | |
| RU UMa | 11:41:40 | +38:28:30 | Mira | 252.46 | M3e-M5e | 8.1-15.0 | 4 | |
| Y Vir | 12:33:52 | -04:25:18 | Mira | 218.43 | M2e-M5e | 8.3-15.0 | 4 | |
| R Vir | 12:38:30 | +06:59:18 | Mira | 145.63 | M3.5IIIe-M8 | 6.1-12.1 | 2 | |
| RS UMa | 12:38:57 | +58:29:03 | Mira | 258.97 | M4e-M6e | 8.3-14.9 | 4 | |
| S UMa | 12:43:57 | +61:05:36 | Mira | 225.87 | S0,9e-S5,9e | 7.1-12.7 | 2 | |
| U Vir | 12:51:06 | +05:33:12 | Mira | 206.64 | M2e-M8e: | 7.4-13.5 | 2 | |
| V UMi | 13:38:41 | +74:18:37 | SRb | 72.0 | M5IIIab | 7.2- 9.1 | 5 | |
| SY Vir | 13:58:38 | -04:34:35 | Mira | 236.65 | M6: | 9.6-13.4 | 1 | |
| HD 123657 | 14:07:56 | +43:51:18 | Lb | M4.5III | 5.25 | 1 | non-LPV | |
| 14:15:38 | +19:11:06 | K1.5III | -0.04 | 1 | r.v. st | |||
| R Boo | 14:37:12 | +26:44:12 | Mira | 223.4 | M3e-M8e | 6.2-13.1 | 5 | |
| Y Lib | 15:11:41 | -06:00:43 | Mira | 275.70 | M5e-M8.2e | 7.6-14.7 | 4 | |
| RT Boo | 15:17:15 | +36:21:34 | Mira | 273.86 | M6.5e-M8e | 8.3-13.9 | 2 | |
| S Ser | 15:21:40 | +14:18:52 | Mira | 371.84 | M5e-M6e | 7.0-14.1 | 1 | |
| S UMi | 15:29:35 | +78:38:00 | Mira | 331.0 | M6e-M9e | 7.5-13.2 | 10 | circum. |
| ST Her | 15:50:47 | +48:29:00 | SRb | 148.0 | M6 | 8.8-10.3 | 1 | |
| RU Her | 16:10:15 | +25:04:14 | Mira | 484.83 | M6e-M9 | 6.8-14.3 | 7 | |
| SS Oph | 16:57:52 | -02:45:42 | Mira | 180.64 | M5e | 7.8-14.5 | 1 | |
| RV Her | 17:00:35 | +31:13:22 | Mira | 205.23 | M2e | 9.0-15.5 | 1 | |
| SY Her | 17:01:29 | +22:28:40 | Mira | 116.91 | M1e-M6e | 8.4-14.0 | 1 | |
| Z Oph | 17:19:32 | +01:30:52 | Mira | 348.7 | K3ep-M7.5 | 7.6-14.0 | 10 | |
| RS Her | 17:21:42 | +22:55:16 | Mira | 219.70 | M4e-M8 | 7.0-13.0 | 3 | |
| RU Oph | 17:32:53 | +09:25:24 | Mira | 202.29 | M3e-M5e | 8.6-14.2 | 1 | |
| 17:43:27 | +04:34:03 | K2III | 2.77 | 6 | r.v. st | |||
| T Her | 18:09:06 | +31:01:16 | Mira | 164.98 | M2,5e-M8e | 6.8-13.7 | 1 | |
| RY Oph | 18:16:37 | +03:41:34 | Mira | 150.41 | M3e-M6 | 7.4-13.8 | 1 | |
| RT Dra | 18:19:26 | +72:40:50 | Mira | 279.41 | M5 | 9.6-13.8 | 14 | circum. |
| SV Her | 18:26:23 | +25:01:35 | Mira | 238.99 | M5e | 9.1-15.1 | 1 | |
| X Oph | 18:38:21 | +08:50:01 | Mira | 328.85 | M5e-M9e | 5.9- 9.2 | 4 | |
| WZ Lyr | 19:02:15 | +47:12:56 | Mira | 376.64 | M9e | 10.6-15.0 | 2 | |
| RU Lyr | 19:12:21 | +41:18:12 | Mira | 371.84 | M6e:-M8e | 9.5-15.9 | 1 | |
| W Aql | 19:15:23 | -07:02:50 | Mira | 490.43 | S3,9e-S6,9e | 7.3-14.3 | 1 | |
| RT Cyg | 19:43:38 | +48:46:41 | Mira | 190.28 | M2e-M8.8eIb | 6.0-13.1 | 7 | |
| 19:46:14 | +10:36:43 | K3II | 2.72 | 3 | r.v. st | |||
| 19:50:34 | +32:54:53 | Mira | 408.05 | S6,2e-S10,4e | 3.3-14.2 | 6 |
| Name | Right Asc. | Declination | Variability | Period | Spectral | Brightness | N | Comments |
| (2000.0) | (2000.0) | Type | (d) | Type | Range | |||
| Z Cyg | 20:01:27 | +50:02:34 | Mira | 263.69 | M5e-M9e | 7.1-14.7 | 1 | |
| S Aql | 20:11:37 | +15:37:13 | SRa | 146.45 | M3e-M5.5e | 8.9-12.8 | 1 | |
| Z Aql | 20:15:11 | -06:09:04 | Mira | 129.22 | M3e | 8.2-14.8 | 1 | |
| WX Cyg | 20:18:34 | +37:26:54 | Mira | 410.45 | C8,2JLi(N3e) | 8.8-13.2 | 2 | |
| T Cep | 21:09:32 | +68:29:28 | Mira | 388.14 | M5.5e-M8.8e | 5.2-11.3 | 6 | |
| RR Aqr | 21:15:01 | -02:53:43 | Mira | 182.45 | M2e-M4e | 9.1-14.4 | 1 | |
| X Peg | 21:21:00 | +14:27:00 | Mira | 201.20 | M2e-M5e | 8.8-14.4 | 1 | |
| SW Peg | 21:22:29 | +21:59:45 | Mira | 396.33 | M4e | 8.0-14.0 | 2 | |
| AX Cep | 21:26:52 | +70:13:18 | Mira | 395.0 | C(N) | 9.5-13.0 | 11 | circum. |
| S Cep | 21:35:13 | +78:37:28 | Mira | 486.84 | C7,4e(N8e) | 7.4-12.9 | 12 | circum. |
| RV Peg | 22:25:38 | +30:28:22 | Mira | 396.80 | M6e | 9.0-15.5 | 1 | |
| AR Cep | 22:51:33 | +85:02:47 | SRb | M4III | 7.0-7.9 | 2 | non-LPV | |
| R Peg | 23:06:39 | +10:32:35 | Mira | 378.1 | M6e-M9e | 6.9-13.8 | 4 | |
| W Peg | 23:19:50 | +26:16:44 | Mira | 345.5 | M6e-M8e | 7.6-13.0 | 5 | |
| S Peg | 23:20:33 | +08:55:08 | Mira | 319.22 | M5e-M8.5e | 6.9-13.8 | 3 | |
| RY Cep | 23:21:14 | +78:57:31 | Mira | 149.06 | Ke-M0e | 8.6-13.6 | 9 | circum. |
| ST And | 23:38:45 | +35:46:17 | SRa | 328.34 | C4,3e-C6,4e | 7.7-11.8 | 5 | |
| R Cas | 23:58:24 | +51:23:18 | Mira | 430.46 | M6e-M10e | 4.7-13.5 | 4 |
A total of 27 observing nights on ELODIE were allocated between 1998, August and 2000, August (more or less one night per month). Approximatively one third of the total observing time was lost mainly because of bad atmospheric conditions, causing interruptions in the phase coverage. About 15-20 stars were observed during each clear night, with typical exposure times of about 25 min yielding a S/N ratio per resolution element at 500 nm up to 150 for the brightest stars. For the faintest and reddest stars, sometimes only the reddest orders recorded a usable signal. But the power of a correlation technique is precisely that it does not require high S/N spectra to deliver useful CCFs (see e.g., Queloz 1995). As indicated in Sect. 2.1, the CCF is computed using orders having an average S/Nratio of at least 2.0.
The log of observations is presented in Table 2: the first and second columns list the civil date and the corresponding Julian date at midnight. The third column gives the code number of the night: each observing night will be subsequently referred to by this number. Only the nights during which at least one star was observed are reported in Table 2.
A total of 315 spectra were collected, i.e. 3-4 spectra per star on average. Some (circumpolar) stars were observed as often as 12 times (SCep), and the majority of variable stars were observed 2-3 times.
For each of the 315 spectra, we compute the CCFs
with the K0III and the M4V default templates. A large variety of CCFs
are observed among LPVs, ranging from the classical single-peak profile to
much more complex profiles (asymmetrical peak, double peak, "noisy''
profiles, etc.). We developed an automatic classification procedure which
classifies the CCFs according to their shape and contrast into a finite
number of archetypes, thus avoiding any subjectivity.
Table 3![]() provides for each observation the CCF code for
the K0- and
M4-templates, together with the night number, the Julian date, the phase
and, when appropriate, the heliocentric radial velocities as derived by a
single or double gaussian fit of the CCF.
The different kinds of CCFs observed are as
follows:
provides for each observation the CCF code for
the K0- and
M4-templates, together with the night number, the Julian date, the phase
and, when appropriate, the heliocentric radial velocities as derived by a
single or double gaussian fit of the CCF.
The different kinds of CCFs observed are as
follows:
Single-peak profiles occur at all phases. 54% of the LPV sample stars showed at least once this kind of profile with the K0-template (28% of the total number of observations). These values amount respectively to 89% and 74% with the M4-template. This cool template thus yields single-peak, well-contrasted CCFs much more often than the K0-template. These profiles are coded "1p'' in Table 3;
A double or asymmetrical peak was observed for 50% of the LPV stars (28% of the total number of observations) with the K0-template. Most of them were not known in the literature to exhibit the line-doubling phenomenon. The doubling is essentially observed around maximum light (between phases -0.1 and 0.3), as can be seen in Fig. 2. With the M4-template, only 23% of sample stars (10% of the total number of observations) showed these kinds of profiles (see Sect. 2.2 of Paper II for a discussion of the physical origin of this difference between the K0- and the M4-templates), and the phases range from -0.2 to 0.6. These profiles are coded "2p'' (double peak) or "ap'' (asymmetrical peak) in Table 3;
| Date of | Julian Date | Night |
| Observations | (2450000+) | Number |
| 1998 Aug., 05-06 | 1031.5 | N1 |
| 1998 Sep., 03-04 | 1060.5 | N2 |
| 1998 Sep., 28-29 | 1085.5 | N3 |
| 1998 Oct., 06-07 | 1093.5 | N4 |
| 1998 Dec., 23-24 | 1171.5 | N5 |
| 1999 Jan., 26-27 | 1205.5 | N6 |
| 1999 Feb., 23-24 | 1233.5 | N7 |
| 1999 Apr., 22-23 | 1291.5 | N9 |
| 1999 May, 19-20 | 1318.5 | N10 |
| 1999 Jul., 05-06 | 1365.5 | N12 |
| 1999 Jul., 26-27 | 1386.5 | N13 |
| 1999 Sep., 02-03 | 1424.5 | N14 |
| 1999 Sep., 28-29 | 1450.5 | N15 |
| 1999 Nov., 16-17 | 1499.5 | N16 |
| 1999 Dec., 16-17 | 1529.5 | N17 |
| 2000 Jan., 10-11 | 1554.5 | N18 |
| 2000 Feb., 22-23 | 1597.5 | N19 |
| 2000 Feb., 23-24 | 1598.5 | N20 |
| 2000 Apr., 17-18 | 1652.5 | N22 |
| 2000 May, 18-19 | 1683.5 | N23 |
| 2000 Jun., 20-21 | 1716.5 | N24 |
| 2000 Jul., 11-12 | 1737.5 | N25 |
| 2000 Aug., 09-10 | 1766.5 | N26 |
| 2000 Aug., 10-11 | 1767.5 | N27 |
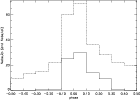 |
Figure 2: Phase distributions (i) for the observations which exhibit a double or an asymmetrical peak with the K0-template (solid line) and (ii) for the total set of observations (dashed line). |
It must be noted that the general structure of the CCFs presented in Figs. 1d and 1e is in fact strikingly similar, the only difference being the respective contrasts of the leftmost and second-to-leftmost peaks. Moreover, a given star (like R Cet; see Table 3 and Fig. 1) may evolve from 1p? CCFs to 2p? CCFs and even to 2p at different phases of its light cycle, thus suggesting that the 1p? and 2p? CCFs of the kind displayed in Figs. 1d and 1e may be intrinsically similar and should in fact be classified together (that conclusion may in fact even be extended to some "np'' profiles, like the one displayed in Fig. 1f whose general structure resembles that of Figs. 1d and 1e). However, in this first analysis of the statistics of the line-doubling phenomenon, it was decided to adopt conservative classification criteria, at the risk of excluding physically-sound data. In particular, the line-doubling statistics presented in Figs. 2, 6-9 relies only on CCFs classified as "2p'' or "ap'' and excludes CCFs classified as "2p?'' and "np''. The possible physical implications of this conservative choice are discussed further in Sect. 4.3.1.1.
Doubtful or noisy profiles were obtained at least once for 61% of the LPV sample stars (44% of the total number of observations) with the K0-template. Although these profiles were found at all phases, they are preferentially observed around minimum light (when the star is fainter and cooler). With the M4-template, the above percentages turn to only 17% of the stars (most of which are the S-type and C-type stars of the sample) and 16% of the total number of observations.
Figure 2 presents the distribution in phase of the
double-peak profiles as compared to the total number of observations. The
striking features exhibited by Fig. 2 are (i) the very
sharp rise in the fraction of double-peak profiles at phase -0.1, (ii) the
total absence of double-peak profiles between phases 0.4 and 0.7, and (iii)
the fraction of double-peak profiles remains almost constant (![]() 40%)
between phases -0.1 and 0.3.
40%)
between phases -0.1 and 0.3.
Another conclusion that can be drawn at this point concerns the interest of the cross-correlation technique for dynamical studies: as already pointed out in 1, the cross-correlation technique provides a powerful tool to extract double lines despite the severe crowding of the spectra of giant stars (see however the discussion of Sect. 4.3.2.1 relative to late-type LPVs). The study of the spectral variations associated with the pulsation of LPV stars has no more to be restricted to the few clean near-IR spectral lines. The much richer visible spectrum is now accessible as well to these studies, opening great potentialities as illustrated for instance by the tomographic technique described in Paper II.
The origin of the line-doubling phenomenon in LPVs has been a long-standing problem (see 1 for a review). The most definitive way to prove that the line doubling is not the result of purely radiative processes but is actually caused by the differential bulk motions in the atmosphere arising from the propagation of a shock wave is to check whether or not the temporal sequence of the line doubling follows the Schwarzschild scenario.
Schwarzschild (1952) developed his scenario for WVir variables, but in principle it can be generalized to any variable star where a shock wave propagates through the photosphere. According to this scenario, the temporal evolution of the intensity of the components of a double line should obey a precise sequence: the intensity of the blue component, formed in deeper, ascending photospheric layers, should increase from zero to maximum, while at the same time the red component, formed in the upper infalling photospheric layers, decreases from maximum to zero (Fig. 1 of 1).
Thanks to a two-month-long monitoring of two LPVs around maximum light, it was shown in 1 that (at least some) LPVs do follow the Schwarzschild scenario. The present set of observations of many LPVs spread over two years enables us to answer the following questions in relation with the line-doubling phenomenon: (i) at which phases does it occur? (ii) does it repeat identically from one cycle to the next? (iii) what is the fraction of LPV stars exhibiting the line doubling phenomenon and what are their distinctive properties?
Although it was shown in 1 that the line profile of the Mira RTCyg followed the Schwarzschild scenario around maximum light, there was no information available about the evolution of the profile at later phases.
In the present sample, the circumpolar Mira SCep (C7, 4e; P=486.84 d according to the GCVS) has a good phase coverage and allows to draw the velocity curve over a full light cycle (Fig. 3): a typical S-shaped curve emerges that is very similar to the curves obtained from the rotation-vibration CO or CN lines in the near-infrared (Hinkle et al. 1997 and references therein). SCep was already known to exhibit the line-doubling phenomenon for those lines (Hinkle & Barnbaum 1996; Fig. 3).
Figure 4 presents the sequence of CCFs obtained for SCep. Several important features must be noted: (i) as seen in Fig. 3, the velocities of the red and blue components are almost identical from one cycle to the next (although their relative intensities change somewhat: compare the profiles at phases 0.95 and 1.96 on Fig. 4); (ii) the center-of-mass velocity derived from the submm CO lines falls in between the red and blue peaks, as expected (Figs. 3 and 4; see also Sect. 4.2); (iii) the velocities derived from the near infrared CO lines (Hinkle et al. 1997) are very similar to those derived from the optical CCFs.
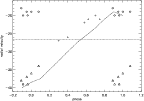 |
Figure 3:
Velocity variations of SCep (cross: single component;
triangles: blue component; diamonds: red component). The dotted line
indicates the center-of-mass velocity (see
Table 4). The velocities between phases 0.8 and 1.1
are shown twice to illustrate the velocity behaviour through
an entire cycle. The dashed line is an eye fit to the
radial-velocity curve of S Cep obtained by Hinkle & Barnbaum (1996)
from CN
|
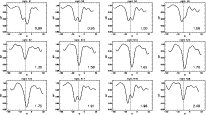 |
Figure 4: Sequence of CCFs for SCep with the default K0III mask. The labels beside each CCF refer to the visual phase computed from the GCVS period and the AAVSO ephemeris. The observing night number is given on top of each panel according to Table 2. The dotted line indicates the center-of-mass velocity (see Table 4). |
The location of the center-of-mass (COM) velocity with respect to the blue and red peaks provides important information about the shock. In the classical Schwarzschild scenario, the COM velocity falls in between the blue and red peaks. It might happen, however, that the shock is not strong enough to oppose the infalling matter. In that case, both peaks would be redshifted with respect to the COM velocity (indicating that the shock is receding in a Eulerian rest frame), as observed for RRLyr stars at some phases (Chadid & Gillet 1996).
This does not occur in SCep, as seen in Figs. 3 and 4 (see also Hinkle & Barnbaum 1996) where the dotted line corresponds to the COM velocity derived by Neri et al. (1998) from sub-mm observations. And seemingly, receding shocks are not observed in Miras at all. Table 4 lists the COM velocity (when available) for LPVs which exhibit a double-peak CCF. The first column gives the star name, the second column the velocities of the blue and red components (extreme value observed), the third column the median of the blue- and red-peak velocities, the fourth column the COM velocity derived from sub-mm observations and the last column the reference for this COM velocity. The COM velocity does always fall in between the blue and red peaks (the median of the red- and blue-peak velocities is in fact blueshifted with respect to the COM velocity, as expected if the shock front is moving outwards), in agreement with the conclusion already reached by Hinkle et al. (1997) from infrared CO lines. It is thus possible to conclude that, unlike in other classes of variable stars such as RRLyrae, shock waves are rather strong in Mira stars.
| GCVS | CCF | median | Center-of-mass | Ref. |
| radial velocities | red/blue | velocity | ||
| (km s-1) | (km s-1) | (km s-1) | ||
| R And | -38/-10 | -24 | -20.3 | 2 |
| R Cet | +22/+48 | +35 | +42.1 | 1 |
| U Ari | -65/-43 | -54 | -46.5 | 1 |
| R Gem | -57/-39 | -48 | -47.6 | 2 |
| S CMi | +50/+72 | +61 | +65.9 | 2 |
| W Aql | -54/-27 | -40.5 | -39.2 | 2 |
| Z Cyg | -179/-160 | -169.5 | -165.8 | 1 |
| AX Cep | -10/+8 | -1 | +0.4 | 1 |
| S Cep | -39/-18 | -28.5 | -26.8 | 3 |
|
References:
1: Groenewegen et al. (1999). 2: Knapp et al. (1998). 3: Neri et al. (1998). |
Not all LPVs exhibit the line doubling (at least when considering only
those CCFs classified as "2p'' or "ap'' as described in
Sect. 3, thus excluding CCFs of the "2p?'' and "np''
kinds; see Fig. 1),
even when observed at maximum light
(see the example of XOph in 1): about 47% of the sample stars observed
at maximum light (between phases -0.10 and 0.10) did not exhibit line
doubling with the K0-template (see Fig. 2).
In an attempt to identify the key stellar parameter(s) governing the
appearance of the line doubling, the distribution of several potentially
relevant parameters is displayed in Fig. 5
(
![]() against the brightness range),
Fig. 6 (period distribution) and
Fig. 7 (distribution of spectral type at maximum
light for oxygen-rich LPVs).
against the brightness range),
Fig. 6 (period distribution) and
Fig. 7 (distribution of spectral type at maximum
light for oxygen-rich LPVs).
There is a weak correlation between the brightness range and the velocity discontinuity (Fig. 5), but the scatter in the relation is very large, albeit similar to that obtained by Hinkle et al. (1997; their Fig. 11) when considering only Miras. The important result from Fig. 5 is that there is no visual-amplitude threshold beyond which line doubling only would occur: instead, small-amplitude as well as large-amplitude Miras are liable to exhibit the line-doubling phenomenon.
The same conclusion is reached when considering the period (Fig. 6) or spectral type (Fig. 7) distributions: double-peak profiles are found among short- as well as long-period LPVs and among early- as well as late-type LPVs. The frequency of double-peak profiles is nevertheless somewhat larger among short-period and early-type LPVs (almost all LPVs with a period less than 250 d and almost all oxygen-rich LPVs with a spectral type earlier than M3 showed line-doubling), suggesting that the line-doubling is restricted to LPVs of small radius (Sect. 4.3.2).
Since the period is correlated with the luminosity and the spectral type
with the effective temperature, and since these two parameters suffice
to define a stellar radius, we investigate the relationship between
the line-doubling phenomenon and the quantity
![]() .
Although this quantity is certainly related to the stellar radius, it
should not be taken at face value since the definition of a stellar radius
for LPVs is a complex task
(e.g. Perrin et al. 1999; Hofmann et al. 2000).
The quantity
.
Although this quantity is certainly related to the stellar radius, it
should not be taken at face value since the definition of a stellar radius
for LPVs is a complex task
(e.g. Perrin et al. 1999; Hofmann et al. 2000).
The quantity ![]() should somehow reflect the stellar size, at
least in a relative sense when comparing one star to another.
should somehow reflect the stellar size, at
least in a relative sense when comparing one star to another.
Luminosities were estimated from the
![]() -P relation of Feast et al. (1989), with no zero-point
correction.
-P relation of Feast et al. (1989), with no zero-point
correction.
Effective temperatures of LPVs are also difficult to derive. Apart from a scarce number of direct determinations from interferometric observations, little is known about the temperature scale of Mira and semi-regular variables. Colour-temperature relations may in principle be used (e.g. Bessell et al. 1998; Alvarez et al. 2000b; Houdashelt et al. 2000), but in practice it is difficult to collect the required set of simultaneous photometric observations for a large sample of LPVs.
In order to estimate
![]() for a number of sample stars as large as possible,
the choice was made to rely on a spectral type-temperature relation,
taking advantage of the fact that almost all LPVs have been given a spectral
type, at least at maximum light. The spectral type/temperature scale of
Perrin et al. (1998) was used for this purpose, with the spectral types at
maximum light taken from the GCVS.
As spectral-type assignments generally carry some degree of subjectivity, so
will the
for a number of sample stars as large as possible,
the choice was made to rely on a spectral type-temperature relation,
taking advantage of the fact that almost all LPVs have been given a spectral
type, at least at maximum light. The spectral type/temperature scale of
Perrin et al. (1998) was used for this purpose, with the spectral types at
maximum light taken from the GCVS.
As spectral-type assignments generally carry some degree of subjectivity, so
will the
![]() values derived from the present procedure.
Their accuracy will be sufficient for the present purpose of identifying a
possible relationship between
values derived from the present procedure.
Their accuracy will be sufficient for the present purpose of identifying a
possible relationship between ![]() and the line-doubling phenomenon.
The derived
and the line-doubling phenomenon.
The derived ![]() values are listed in Table 3.
values are listed in Table 3.
Figure 8 shows the ![]() distribution for two sub-samples:
(i) the stars for which a double or asymmetrical peak was obtained
with the K0-template (solid line);
(ii) the stars for which a double or asymmetrical peak was not
obtained, even when observed at maximum light (dashed line).
Semi-regular variables (as they do not follow the period-luminosity
relation) and carbon stars (as they do not obey the oxygen-rich spectral
type/temperature relation) are excluded from Fig. 8.
Stars with a double peak are clearly separated from single-peak stars.
A large majority of small-size stars (
distribution for two sub-samples:
(i) the stars for which a double or asymmetrical peak was obtained
with the K0-template (solid line);
(ii) the stars for which a double or asymmetrical peak was not
obtained, even when observed at maximum light (dashed line).
Semi-regular variables (as they do not follow the period-luminosity
relation) and carbon stars (as they do not obey the oxygen-rich spectral
type/temperature relation) are excluded from Fig. 8.
Stars with a double peak are clearly separated from single-peak stars.
A large majority of small-size stars (
![]() )
present a double
peak, whereas large-size stars (
)
present a double
peak, whereas large-size stars (
![]() )
are almost all
single-peak stars. Such a segregation is quite remarkable given the various
sources of uncertainty on
)
are almost all
single-peak stars. Such a segregation is quite remarkable given the various
sources of uncertainty on ![]() .
It accounts for the results of 1,
namely the occurrence of line-doubling in RTCyg (
.
It accounts for the results of 1,
namely the occurrence of line-doubling in RTCyg (
![]() )
but not in XOph (
)
but not in XOph (
![]() ).
).
The predictive power of Fig. 8 is of interest in relation with abundance analyses of LPVs in external systems, where the available spectral resolution may not be high enough to reveal the line doubling. This may introduce large errors on the abundances, and Fig. 8 reveals that such a risk is highest for warm and short-period LPVs.
Figure 8, which shows that the line-doubling phenomenon
is only present in the most compact Mira stars, is one of the
most striking result of this paper.
At this stage, two interpretations of this result are still possible:
(i) it is an artefact of the use of the K0III template which is not
able to reveal the double peaks in the
LPVs with large ![]() which have very late and crowded spectra;
which have very late and crowded spectra;
(ii) the observed segregation in terms of ![]() is real and related
to the physics of the shocks in LPVs.
is real and related
to the physics of the shocks in LPVs.
These two possibilities are discussed in turn in the remainder of this
section.
Since the K0III
template better matches the spectra of early-type LPVs than of
late-type LPVs,
it may possibly be more efficient
in detecting line-doubling in early-type LPVs, thus possibly causing a bias
against the detection of line doubling in large-![]() LPVs.
The interpretation of Fig. 8 simply in terms of such
a selection bias caused by the use of too warm a template appears
however too simplistic, as we now discuss.
LPVs.
The interpretation of Fig. 8 simply in terms of such
a selection bias caused by the use of too warm a template appears
however too simplistic, as we now discuss.
Since the cooler M4V template![]() constitutes a better match to the crowded
spectra of late-type LPVs, one might have
expected a better efficiency of detection of line doubling with that template.
We already
showed in Sect. 3 that even less
double-peaked
CCFs are found with the M4V template than with the
K0III one. Figure 9 shows that the segregation of
single/double peaks in terms of
constitutes a better match to the crowded
spectra of late-type LPVs, one might have
expected a better efficiency of detection of line doubling with that template.
We already
showed in Sect. 3 that even less
double-peaked
CCFs are found with the M4V template than with the
K0III one. Figure 9 shows that the segregation of
single/double peaks in terms of ![]() remains basically the same with
the M4V template as with the K0III template.
remains basically the same with
the M4V template as with the K0III template.
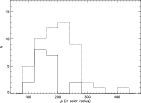 |
Figure 9: Same as Fig. 8 for the M4-template. |
Nevertheless, by considering infrared CO
![]() lines around
1.6
lines around
1.6 ![]() m, Hinkle et al. (1984, 1997) reported line doubling around
maximum light for several
late-type
LPVs
with large
m, Hinkle et al. (1984, 1997) reported line doubling around
maximum light for several
late-type
LPVs
with large ![]() (Table 5) that were flagged as 1p or 1p? with the K0III
and M4V templates.
Thus line doubling is definitely present at least in
some of those stars as well.
(Table 5) that were flagged as 1p or 1p? with the K0III
and M4V templates.
Thus line doubling is definitely present at least in
some of those stars as well.
Quite interestingly, Hinkle et al. (1984)
note that in these late-type LPVs line doubling is more easily seen
in the deep photospheric layers probed by the
infrared CO
![]() lines around
1.6
lines around
1.6 ![]() m than in the higher layers where the blue-violet absorption
lines form. In an attempt to uncover double-peak CCFs in late-type
LPVs as well, their spectra were correlated with various masks
(constructed with the procedure of Baranne et al. 1979)
mimicking F0V, G2V (solar), K4III (81 Gem) and M4III
(HD 123657) spectra.
m than in the higher layers where the blue-violet absorption
lines form. In an attempt to uncover double-peak CCFs in late-type
LPVs as well, their spectra were correlated with various masks
(constructed with the procedure of Baranne et al. 1979)
mimicking F0V, G2V (solar), K4III (81 Gem) and M4III
(HD 123657) spectra.
While the cool masks (M4V and M4III) yield very clean, albeit single, CCFs, interesting results are indeed obtained with the warm F0V and G2V masks, which are expected to probe deeper layers. They reveal asymmetric, or even double-peak, CCFs (Table 5 and Fig. 10), with velocities similar to those obtained by Hinkle et al. (1984). There is however a drawback to the application of warm templates to cool LPVs. Since the warm templates contain far fewer lines than the spectrum of cool LPVs, many spurious secondary peaks must be expected in their CCFs. These peaks correspond to the chance coincidence occurring between the mask and the forest of lines flanking the lines actually probed by the mask. This situation is well illustrated by Fig. 10 which compares the CCFs obtained with different masks applied on the late-type LPV R Cas and on the synthetic spectrum of a static 2800 K model. The latter CCFs make it possible to identify the spurious secondary peaks caused by the correlation noise invoked above. By comparison, the CCFs of R Cas obtained with the warm templates exhibit the same spurious peaks as the 2800 K model, except that a supplementary blue component appears around 0 km s-1 (see also Table 5). This component not observed in the CCF of a static spectrum may thus tentatively be related to the dynamics of the envelope of R Cas.
| CO
|
CCF | K0III | M4V | F0V | ||||||||
| Spect. type | Phase | Phase | night | |||||||||
| R And | S3,5e - S8,8e | 217 | 0.96 | -29.3/-5.7 | 0.98 | N26 | 2p | -38.3/-10.2 | 1p | -9.5 | 2p | -38.1/-9.8 |
| R Cas | M6e - M10e | 282 | 0.03 | +5.9/+28.5 | 1.02 | N13 | 1p? | - | 1p | +22.7 | 2p? | 0/+21.7 |
| T Cep | M5.5e - M8.8e | 238 | 0.87 | -19.2/-2.4 | 1.91 | N23 | np | - | 1p | -14.9 | 1pa | -19.5/-10.3 |
| o Cet | M5e - M9e | 150 | 0.96 | +44.7/+67.8 | 1.91 | N15 | 1p? | - | 1p | +61.7 | 2p? | +38.4/+57.9 |
Many of the LPVs with large ![]() that were originally classified as
1p or 1p? from their K0III CCF actually behave like R Cas as shown in
Fig. 10.
that were originally classified as
1p or 1p? from their K0III CCF actually behave like R Cas as shown in
Fig. 10.
In conclusion, double-peaked
CCFs may actually be present in LPVs with large ![]() as well.
We nevertheless stress that this conclusion must be subject to
caution, since these double-peak CCFs - if real -
are quite difficult to detect because of the crowded
nature of their parent spectra.
In Sect. 4.3.2.2, we discuss the possibility that this
difficult detection may also be caused partly by the
secondary peaks being truly weaker in stars
with large
as well.
We nevertheless stress that this conclusion must be subject to
caution, since these double-peak CCFs - if real -
are quite difficult to detect because of the crowded
nature of their parent spectra.
In Sect. 4.3.2.2, we discuss the possibility that this
difficult detection may also be caused partly by the
secondary peaks being truly weaker in stars
with large ![]() due to weaker shocks.
due to weaker shocks.
The behaviour of the H![]() emission line in our sample of
LPVs provides important clues to help us interpret, in terms of the properties
of the shocks in LPVs, the result that the
line-doubling phenomenon
is conspicuous only in the most compact LPVs.
emission line in our sample of
LPVs provides important clues to help us interpret, in terms of the properties
of the shocks in LPVs, the result that the
line-doubling phenomenon
is conspicuous only in the most compact LPVs.
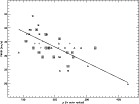 |
Figure 11:
Full width at half maximum of the H |
The first important result regarding H![]() is that it appears in emission around maximum light
for all LPVs in our sample
(see Fig. 11 discussed
below). Since H
is that it appears in emission around maximum light
for all LPVs in our sample
(see Fig. 11 discussed
below). Since H![]() is considered as a good signature of the
presence of shocks in those atmospheres,
the above result thus suggests that double-peak CCFs, being another signature
of shocks, should be observed as well in all
LPVs.
We argue in the present section that the behaviour of H
is considered as a good signature of the
presence of shocks in those atmospheres,
the above result thus suggests that double-peak CCFs, being another signature
of shocks, should be observed as well in all
LPVs.
We argue in the present section that the behaviour of H![]() and the statistics of double-peak CCFs in LPVs may be reconciled
by realizing that
the shock strength
becomes smaller in stars of larger
and the statistics of double-peak CCFs in LPVs may be reconciled
by realizing that
the shock strength
becomes smaller in stars of larger ![]() .
Figure 11 presents the full width at
half maximum (FWHM) of the H
.
Figure 11 presents the full width at
half maximum (FWHM) of the H![]() emission line vs. the stellar size
emission line vs. the stellar size
![]() .
We observe a trend of decreasing H
.
We observe a trend of decreasing H![]() FWHMs
with increasing stellar sizes
FWHMs
with increasing stellar sizes ![]() .
Among the Balmer lines, H
.
Among the Balmer lines, H![]() is the best
indicator of the energy transferred by the shock to the gas,
since H
is the best
indicator of the energy transferred by the shock to the gas,
since H![]() suffers the least from
mutilations induced by molecular absorptions
(the TiO line absorption and H2 scattering
coefficients are indeed minimum around H
suffers the least from
mutilations induced by molecular absorptions
(the TiO line absorption and H2 scattering
coefficients are indeed minimum around H![]() ;
Gillet 1988b).
Its width measures the temperature in the post-shock gas
where the Balmer
emission lines form. The heating in the shock wake must in turn be
related to the energy carried by the shock.
;
Gillet 1988b).
Its width measures the temperature in the post-shock gas
where the Balmer
emission lines form. The heating in the shock wake must in turn be
related to the energy carried by the shock.
Similarly, the difficulty of detecting double-peaked CCFs
in stars with large ![]() might also somehow relate to
the weakness of the shocks in those stars (as inferred from their
smaller H
might also somehow relate to
the weakness of the shocks in those stars (as inferred from their
smaller H![]() FWHMs), although a definite proof
of this statement would require solving of the equation of radiative
transfer in dynamical atmospheres, with detailed shock models.
FWHMs), although a definite proof
of this statement would require solving of the equation of radiative
transfer in dynamical atmospheres, with detailed shock models.
Self-consistent dynamical models of LPV atmospheres are clearly necessary to confirm that the strongest shocks only occur in the more compact Mira stars. In any case, the relation of the shock strength with the stellar size empirically revealed by Fig. 11 will have to be accounted for by future dynamical models of LPV atmospheres.
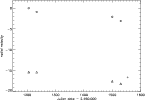 |
Figure 15: Radial-velocity curve of SCam with the default K0III mask. Symbols are as in the last panel of Fig. 3. Notice the long-term trend, unlike the situation observed for SCep in Fig. 3. |
Observations spread over several cycles are available for some stars and allow us to address the questions of (i) the repeatability of the line doubling from one cycle to the other (as far as the relative peak intensities and velocities are concerned), and (ii) the frequency of spectroscopic binaries among LPVs. In Figs. 12 and 13 are presented the CCFs obtained for RGem and STAnd respectively, at maximum light for two consecutive pulsational cycles. The CCF profile is remarkably similar from one cycle to the other, with the same velocities to within 1 km s-1 for the blue and red peaks. This result, based on only two stars, may not necessarily be extrapolated to all LPVs.
By contrast, the situation observed in SCam (Fig. 14) is quite interesting: although the CCF shape is almost identical for similar phases of two consecutive cycles, it is shifted by about 3 km s-1. Figure 15 shows the radial-velocity curve of SCam: the common velocity shift for the blue and red peaks from one cycle to the next is quite clear, and flags this star as a suspected binary. The example of S Cam only serves to illustrate the method, since to confirm the binary nature of S Cam would still require us to prove that the phases compared in Fig. 14 are really identical, i.e. that the period is constant (this is not necessarily the case for a SRa variable like S Cam) and that the observed radial-velocity shift is larger than the typical cycle-to-cycle scatter.
Little is known about the binary frequency among LPVs (see Jorissen 2001 for a
recent review). As pointed out in
Sect. 4.1 and Fig. 3, the
radial-velocity variations induced by the LPV pulsation are large
(
![]() km s-1 over
km s-1 over ![]() 1 y) as compared to the
variations expected for the orbital motion of a large giant in a relatively
wide binary system (
1 y) as compared to the
variations expected for the orbital motion of a large giant in a relatively
wide binary system (
![]() 5 km s-1 over several years).
5 km s-1 over several years).
However, the example of SCam provides a hint on how binary systems may be found among LPVs exhibiting a double-peak CCF: a similar velocity shift observed for both the red and blue components from one cycle to the other may be indicative of a binary motion. Such a strategy is unfortunately quite time-consuming as only double-peak CCFs obtained around the same pulsational phase in successive cycles may be used, and is obviously not applicable to those LPVs exhibiting only a single-peak CCF.
In our sample of 81 LPVs, 43 showed a double-peak CCF at least once with
the K0-template (Table 3), but only 9 could be observed at about the same phase
(within 0.1) in consecutive cycles and exhibited double-peak CCFs (namely
YAnd, VTau, SCam, RGem, YVir, ZOph, RTCyg, SCep and
STAnd).
In this sample, the average absolute velocity shift between similar phases in
consecutive cycles amounts to
![]() (rms) km s-1
and
(rms) km s-1
and
![]() (rms) km s-1 when removing the suspected binaries SCam
(having
(rms) km s-1 when removing the suspected binaries SCam
(having
![]() and 2.8 km s-1,
and
and 2.8 km s-1,
and
![]() and 2.2 km s-1) and, somewhat
less likely, Y Vir (having
and 2.2 km s-1) and, somewhat
less likely, Y Vir (having
![]() km s-1,
and
km s-1,
and
![]() km s-1).
No other star in the above list shows a significant signature of binary motion.
km s-1).
No other star in the above list shows a significant signature of binary motion.
For the stars not suspected of being binaries, the red- and blue-peak
shifts from one cycle to the next may sometimes be quite different, since the
average
![]() ,
instead of being close
to 0, amounts to
,
instead of being close
to 0, amounts to
![]() (rms) km s-1.
(rms) km s-1.
The most striking result relative to the
statistics of occurrence of the line-doubling phenomenon in a sample of
81 LPVs of various periods, spectral types and
brightness ranges is the fact that the compact LPVs are more
prone to exhibit the line-doubling phenomenon than large-size LPVs
(at
least when comparing their K0III CCFs).
The possibility that this segregation is an artefact of the use of the K0III
template may not be totally excluded, since
warmer masks (F0V and G2V) applied to the most extended and
coolest LPVs yield asymmetric
cross-correlation functions. This suggests that line doubling is
occurring in those stars as well. Although a firm conclusion on this
point is hampered by the large correlation noise present in the
CCFs of cool LPVs obtained with warm masks, the occurrence of line
doubling in those stars is confirmed by the double
CO
![]() lines observed around 1.6
lines observed around 1.6 ![]() m by Hinkle
et al. (1984).
Moreover, the H
m by Hinkle
et al. (1984).
Moreover, the H![]() line in emission, which is another signature of the
presence of shocks, is observed as well
in the most extended stars,
although with a somewhat narrower profile. This is an indication that the shock is
weaker in extended than in compact LPVs, which may also contribute to
the difficulty of detecting line doubling in cool, extended LPVs.
line in emission, which is another signature of the
presence of shocks, is observed as well
in the most extended stars,
although with a somewhat narrower profile. This is an indication that the shock is
weaker in extended than in compact LPVs, which may also contribute to
the difficulty of detecting line doubling in cool, extended LPVs.
Stars with double absorption lines around maximun light exhibit S-shaped radial-velocity curves similar to the one observed for infrared lines.
A comparison with the center-of-mass (COM) velocity obtained from submm CO lines originating in the circumstellar envelope reveals that the median velocity between the red and blue peaks is blueshifted with respect to the COM velocity, as expected if the shock moves upwards.
Acknowledgements
RA benefits of a TMR "Marie Curie'' Fellowship at ULB. A.J. is Research Associate from the Fonds National de la Recherche Scientifique (Belgium). We thank J. Mattei for providing data from the AAVSO database. This program would not have been possible without the generous allocation of telescope time at the Observatoire de Haute-Provence (operated by CNRS, France). We tank S. Udry for providing us with F0V and G2V templates.
| Name | Night | Julian Date | Phase | K0-template | M4-template | |
| ( |
Number | (2450000+) | ||||
| SV And | 211 | N2 | 1060.5 | 0.04 | 1p (-93.1) | 1p (-91.8) |
| N13 | 1386.5 | 1.08 | 2p? | 1p (-90.2) | ||
| T And | 181 | N4 | 1093.5 | 0.95 | 2p (-95.5/-79.2) | 1p (-83.0) |
| N15 | 1450.5 | 2.11 | np | 1p (-84.8) | ||
| R And | 217 | N26 | 1766.5 | 0.98 | 2p (-38.3/-10.2) | 1p (-9.5) |
| Y Cep | 217 | N26 | 1766.5 | 0.00 | np | 1p (-6.0) |
| U Psc | 135 | N27 | 1767.5 | 0.09 | 1p (+37.5) | 1p (+36.8) |
| R Psc | 196 | N4 | 1093.5 | 0.03 | 1p (-45.4) | 1p (-46.0) |
| N15 | 1450.5 | 0.98 | 1p (-44.5) | 1p (-45.0) | ||
| N16 | 1499.5 | 1.12 | np | 1p (-45.5) | ||
| N17 | 1529.5 | 1.20 | 1p (-46.8) | 1p (-45.4) | ||
| N27 | 1767.5 | 1.90 | 1p (-43.6) | 1p (-44.4) | ||
| Y And | 150 | N2 | 1060.5 | 0.03 | 2p (-15.8/+0.9) | 1p (-4.0) |
| N3 | 1085.5 | 0.14 | ap (-13.7/-1.2) | 1p (-4.5) | ||
| N16 | 1499.5 | 2.02 | 2p (-16.5/+4.7) | 1p (+2.8) | ||
| N17 | 1529.5 | 2.15 | 2p (-14.8/+3.1) | 1p (+2.1) | ||
| N18 | 1554.5 | 2.27 | np | 1p (+2.2) | ||
| o Cet | 150 | N4 | 1093.5 | 0.92 | 2p? | 1p (+59.1) |
| N15 | 1450.5 | 1.91 | 1p? | 1p (+61.7) | ||
| N17 | 1529.5 | 2.14 | 1p (+59.7) | 1p (+61.6) | ||
| R Cet | 132 | N3 | 1085.5 | 0.07 | 2p (+31.7/+48.2) | 1p (+45.2) |
| N4 | 1093.5 | 0.30 | 2p? | 1p (+46.1) | ||
| N7 | 1233.5 | 0.96 | 1p (+45.5) | 1p (+44.1) | ||
| N13 | 1386.5 | 1.88 | 1p (+47.5) | 1p (+47.4) | ||
| N15 | 1450.5 | 2.26 | 2p (+21.7/+44.5) | 1p (+46.0) | ||
| N18 | 1554.5 | 2.89 | 1p? | 1p (+45.0) | ||
| N19 | 1597.5 | 3.15 | 1p? | 1p (+44.8) | ||
| U Cet | 148 | N27 | 1767.5 | 0.01 | np | 1p (-38.3) |
| R Tri | 175 | N15 | 1450.5 | 0.30 | np | ap (+53.3/+65.3) |
| N17 | 1529.5 | 0.60 | np | 1p (+58.6) | ||
| N19 | 1597.5 | 0.85 | 1p (+59.7) | 1p (+61.0) | ||
| U Ari | 214 | N2 | 1060.5 | 0.00 | 2p? | 1p (-43.8) |
| N3 | 1085.5 | 0.07 | np | 1p (-44.2) | ||
| N15 | 1450.5 | 1.05 | 1p (-40.4) | 1p (-40.3) | ||
| N17 | 1529.5 | 1.26 | 2p (-64.6/-42.9) | 1p (-40.3) | ||
| N18 | 1554.5 | 1.33 | np | 1p (-40.0) | ||
| SS Cep | N15 | 1450.5 | 1.56: | 1p (-49.0) | 1p (-49.0) | |
| N18 | 1554.5 | 2.71: | 1p (-48.3) | 1p (-48.3) | ||
| N19 | 1597.5 | 3.19: | 1p (-48.2) | 1p (-47.7) | ||
| R Tau | 212 | N3 | 1085.5 | 0.01 | 1p (+31.6) | 1p (+32.1) |
| N15 | 1450.5 | 1.15 | np | 1p (+27.0) | ||
| N17 | 1529.5 | 1.40 | np | 1p (+29.2) | ||
| N20 | 1598.5 | 1.61 | np | 1p (+29.4) | ||
| V Tau | 111 | N4 | 1093.5 | 0.08 | 2p (+57.5/+76.8) | 2p (+57.2/+74.8) |
| N15 | 1450.5 | 2.01 | 2p (+56.0/+77.8) | 1p (+73.8) | ||
| N17 | 1529.5 | 2.48 | np | 1p (+74.0) | ||
| N20 | 1598.5 | 2.89 | 1p (+77.4) | 1p (+77.4) | ||
| R Aur | 292 | N4 | 1093.5 | 0.54 | np | 1p (-2.5) |
| N15 | 1450.5 | 1.25 | np | 1p (+5.8) | ||
| N20 | 1598.5 | 1.57 | np | 1p (+4.4) | ||
| W Aur | 171 | N3 | 1085.5 | 0.95 | 1p (-131.3) | 1p (-132.6) |
| N19 | 1597.5 | 2.82 | np | ap (-140.5/-130.4) | ||
| RU Aur | 326 | N3 | 1085.5 | 0.97 | np | 1p (-21.9) |
| N18 | 1554.5 | 1.98 | 1p (-18.9) | 1p (-20.1) | ||
| N19 | 1597.5 | 2.07 | np | 1p (-19.5) | ||
| S Cam | N6 | 1205.5 | 0.07 | 2p (-15.4/+0.0) | np | |
| N7 | 1233.5 | 0.15 | 2p (-15.4/-0.9) | np | ||
| N17 | 1529.5 | 1.06 | 2p (-17.6/-2.1) | np | ||
| N18 | 1554.5 | 1.13 | 2p (-18.2/-3.1) | np | ||
| N19 | 1597.5 | 1.27 | 1p (-16.6) | np | ||
| N6 | 1205.5 | -- | 1p (+24.3) | 1p (+23.3) | ||
| U Ori | 257 | N4 | 1093.5 | 0.01 | 1p (-23.7) | 1p (-23.7) |
| N17 | 1529.5 | 1.11 | np | 1p (-22.4) | ||
| N18 | 1554.5 | 1.18 | np | 1p (-23.3) | ||
| N20 | 1598.5 | 1.30 | np | 1p (-23.4) |
| Name | Night | Julian Date | Phase | K0-template | M4-template | |
| ( |
Number | (2450000+) | ||||
|
|
N6 | 1205.5 | -- | 1p (+9.0) | 1p (+9.0) | |
| X Aur | 125 | N20 | 1598.5 | 0.42 | 1p (-23.6) | 1p (-19.1) |
| N23 | 1683.5 | 0.94 | 1p (-16.7) | 1p (-16.1) | ||
| N6 | 1205.5 | -- | 1p (+54.5) | 1p (+54.4) | ||
| SU Cam | 198 | N4 | 1093.5 | 0.03 | 2p? | 1p (-58.0) |
| N6 | 1205.5 | 0.32 | np | 1p (-57.5) | ||
| N7 | 1233.5 | 0.41 | np | 2p (-67.3/-56.6) | ||
| N17 | 1529.5 | 1.45 | np | 1p (-61.9) | ||
| N18 | 1554.5 | 1.54 | np | 1p (-63.7) | ||
| N19 | 1597.5 | 1.69 | np | 1p (-62.6) | ||
| N22 | 1652.5 | 1.88 | 1p (-61.6) | 1p (-60.9) | ||
| N23 | 1683.5 | 1.99 | 1p (-63.3) | 1p (-60.9) | ||
| X Gem | 189 | N20 | 1598.5 | 0.60 | np | 1p (+39.9) |
| N22 | 1652.5 | 0.81 | 1p (+42.0) | 1p (+42.6) | ||
| N23 | 1683.5 | 0.92 | 1p (+40.7) | 1p (+42.5) | ||
| X Mon | N22 | 1652.5 | 0.94 | ap (+154.7/+171.5) | 1p (+167.0) | |
| R Gem | 194 | N4 | 1093.5 | 0.99 | 2p (-56.6/-38.8) | 2p (-58.2/-39.2) |
| N6 | 1205.5 | 1.21 | 2p (-54.9/-40.5) | 2p (-53.0/-39.2) | ||
| N7 | 1233.5 | 1.29 | 2p (-55.0/-43.0) | np | ||
| N17 | 1529.5 | 2.09 | 2p (-55.8/-39.2) | 2p? | ||
| N18 | 1554.5 | 2.15 | 2p (-55.6/-40.5) | np | ||
| N19 | 1597.5 | 2.27 | 2p (-55.8/-41.7) | 1p? | ||
| N22 | 1652.5 | 2.42 | 1p? | 1p? | ||
| R CMi | N20 | 1598.5 | 0.58 | 1p (+45.9) | 1p? | |
| S CMi | 241 | N6 | 1205.5 | 0.02 | np | 1p (+67.5) |
| N7 | 1233.5 | 0.10 | 1p (+67.6) | 1p (+68.7) | ||
| N17 | 1529.5 | 0.99 | 1p (+70.9) | 1p (+71.5) | ||
| N18 | 1554.5 | 1.07 | 2p (+49.6/+72.5) | 1p (+72.9) | ||
| N19 | 1597.5 | 1.20 | 2p? | 1p (+73.3) | ||
| N6 | 1205.5 | -- | 1p (-21.7) | 1p (-21.6) | ||
| 81 Gem | N6 | 1205.5 | -- | 1p (+77.3) | 1p (+77.4) | |
| R Cnc | 254 | N3 | 1085.5 | 0.96 | np | 1p (+28.0) |
| N17 | 1529.5 | 2.19 | 1p? | 1p (+31.7) | ||
| N18 | 1554.5 | 2.26 | 1p? | 1p (+32.1) | ||
| N20 | 1598.5 | 2.38 | np | 1p (+30.4) | ||
| N22 | 1652.5 | 2.53 | np | ap (+19.5/+29.4) | ||
| X UMa | 161 | N6 | 1205.5 | 0.05 | 2p (-90.8/-77.0) | 1p (-79.0) |
| N7 | 1233.5 | 0.16 | 2p? | 1p (-79.1) | ||
| N17 | 1529.5 | 1.35 | np | 1p? | ||
| N22 | 1652.5 | 1.85 | np | 1p (-80.4) | ||
| HD 76830 | N6 | 1205.5 | -- | 1p (+23.2) | 1p (+23.1) | |
| UZ Hya | 173 | N6 | 1205.5 | 0.98 | ap (+30.1/+46.3) | 1p (+40.4) |
| N7 | 1233.5 | 1.09 | ap (+28.6/+44.8) | 2p (+27.4/+41.0) | ||
| N17 | 1529.5 | 2.22 | 2p? | 1p (+40.3) | ||
| N18 | 1554.5 | 2.32 | np | 2p (+28.5/+41.1) | ||
| N20 | 1598.5 | 2.49 | np | 1p (+34.1) | ||
| R Leo | 231 | N19 | 1597.5 | 0.76 | np | 1p (+5.2) |
| N22 | 1652.5 | 0.94 | np | 1p (+7.1) | ||
| N23 | 1683.5 | 1.04 | np | 1p (+7.5) | ||
| S LMi | 148 | N20 | 1598.5 | 0.99 | 2p (-14.8/+0.1) | ap (-13.4/-6.2) |
| N22 | 1652.5 | 1.22 | 1p (-12.1) | 1p (-9.2) | ||
| V Leo | 193 | N6 | 1205.5 | 0.05 | ap (-26.5/-16.4) | 1p (-22.1) |
| N7 | 1233.5 | 0.16 | np | 1p (-21.8) | ||
| N17 | 1529.5 | 1.24 | np | 1p (-21.4) | ||
| N18 | 1554.5 | 1.33 | np | 1p (-19.8) | ||
| R UMa | 181 | N9 | 1291.5 | 0.03 | 2p (+14.2/+36.5) | 1p (+35.1) |
| N17 | 1529.5 | 0.82 | np | 1p (+33.7) | ||
| N18 | 1554.5 | 0.90 | 1p? | 1p (+34.1) | ||
| N19 | 1597.5 | 1.04 | 1p (+35.2) | 1p (+33.8) | ||
| RU UMa | 162 | N6 | 1205.5 | 0.97 | np | 1p (-56.2) |
| N7 | 1233.5 | 1.08 | 2p (-67.5/-54.8) | 1p (-56.1) | ||
| N17 | 1529.5 | 2.26 | np | 1p (-57.6) | ||
| N18 | 1554.5 | 2.35 | np | np | ||
| Y Vir | 142 | N7 | 1233.5 | 0.99 | 2p (+3.4/+16.6) | 1p (+13.3) |
| N18 | 1554.5 | 2.46 | np | 2p? | ||
| N20 | 1598.5 | 2.66 | np | 1p (+7.3) | ||
| N22 | 1652.5 | 2.90 | 2p (+0.4/+14.4) | 1p (+9.1) | ||
| R Vir | 117 | N23 | 1683.5 | 0.92 | ap (-35.3/-23.3) | 1p (-32.8) |
| N24 | 1716.5 | 1.14 | ap (-35.1/-23.0) | 1p (-31.0) |
| Name | Night | Julian Date | Phase | K0-template | M4-template | |
| ( |
Number | (2450000+) | ||||
| RS UMa | 172 | N6 | 1205.5 | 0.10 | ap (-31.8/-18.1) | 1p (-30.3) |
| N7 | 1233.5 | 0.20 | 2p (-37.3/-23.8) | 1p (-29.9) | ||
| N18 | 1554.5 | 1.44 | np | 1p (-25.8) | ||
| N24 | 1716.5 | 2.07 | 1p (-23.3) | 1p (-23.6) | ||
| S UMa | 133 | N19 | 1597.5 | 0.91 | ap (-1.0/+14.0) | ap (-1.8/+11.6) |
| N22 | 1652.5 | 1.15 | 1p (-7.7) | 1p (-7.5) | ||
| U Vir | 137 | N20 | 1598.5 | 0.06 | 2p (-56.3/-41.7) | 2p (-56.3/-44.5) |
| N22 | 1652.5 | 0.32 | np | 1p (-47.8) | ||
| V UMi | N7 | 1233.5 | 0.99: | 1p (-171.2) | 1p (-171.9) | |
| N18 | 1554.5 | 5.44: | 1p (-165.9) | 1p (-167.0) | ||
| N19 | 1597.5 | 6.04: | 1p (-170.3) | 1p (-171.8) | ||
| N22 | 1652.5 | 6.81: | 1p (-168.7) | 1p (-166.7) | ||
| N24 | 1716.5 | 7.69: | 1p (-168.3) | 1p (-166.0) | ||
| SY Vir | 197 | N24 | 1716.5 | 0.05 | ap (+11.2/+21.7) | 1p (+17.9) |
| HD 123657 | N6 | 1205.5 | -- | 1p (-37.3) | 1p (-37.5) | |
| N19 | 1597.5 | -- | 1p (-5.3) | 1p (-5.2) | ||
| R Boo | 151 | N7 | 1233.5 | 0.98 | 2p (-66.4/-49.1) | ap (-62.8/-51.9) |
| N9 | 1291.5 | 1.24 | np | 1p (-55.1) | ||
| N18 | 1554.5 | 2.41 | np | ap (-64.1/-53.8) | ||
| N19 | 1597.5 | 2.61 | np | 1p (-59.7) | ||
| N22 | 1652.5 | 2.85 | 1p (-55.2) | 1p (-56.5) | ||
| Y Lib | 194 | N6 | 1205.5 | 0.98 | np | 2p (-2.9/+7.1) |
| N7 | 1233.5 | 1.08 | 1p? | 1p (+3.1) | ||
| N19 | 1597.5 | 2.40 | np | 1p (+6.4) | ||
| N24 | 1716.5 | 2.83 | np | 1p (+4.3) | ||
| RT Boo | 215 | N20 | 1598.5 | 0.05 | 1p (+34.2) | 1p (+37.3) |
| N23 | 1683.5 | 0.36 | np | 1p (+34.4) | ||
| S Ser | 232 | N25 | 1737.5 | 0.01 | np | 1p (+9.2) |
| S UMi | 241 | N1 | 1031.5 | 0.69 | np | 1p (-53.8) |
| N6 | 1205.5 | 1.22 | np | np | ||
| N7 | 1233.5 | 1.30 | np | ap (-56.5/-48.3) | ||
| N9 | 1291.5 | 1.48 | np | 1p (-54.7) | ||
| N12 | 1365.5 | 1.70 | np | 1p (-52.4) | ||
| N13 | 1386.5 | 1.76 | np | 1p (-51.5) | ||
| N14 | 1424.5 | 1.88 | np | 1p (-50.0) | ||
| N20 | 1598.5 | 2.40 | np | ap (-59.2/-51.0) | ||
| N22 | 1652.5 | 2.57 | np | 1p (-55.6) | ||
| N24 | 1716.5 | 2.76 | 1p? | 1p (-52.8) | ||
| ST Her | N7 | 1233.5 | -- | 1p (-24.3) | 1p (-22.8) | |
| RU Her | 303 | N9 | 1291.5 | 0.02 | 1p (-25.0) | 1p (-25.2) |
| N10 | 1318.5 | 0.08 | 1p (-26.0) | 1p (-25.1) | ||
| N12 | 1365.5 | 0.17 | np | 1p (-25.0) | ||
| N20 | 1598.5 | 0.65 | np | 1p (-29.9) | ||
| N23 | 1683.5 | 0.83 | np | 1p (-28.3) | ||
| N24 | 1716.5 | 0.90 | np | 1p (-28.0) | ||
| N26 | 1766.5 | 1.00 | 1p? | 1p (-27.1) | ||
| SS Oph | 150 | N24 | 1716.5 | 0.98 | 2p (-41.9/-28.2) | 1p (-31.5) |
| RV Her | 137 | N24 | 1716.5 | 0.95 | 2p? | 1p (-47.9) |
| SY Her | 93 | N23 | 1683.5 | 0.09 | ap (+21.6/+36.6) | 1p (+31.2) |
| Z Oph | 143 | N1 | 1031.5 | 0.08 | 2p (-96.0/-77.2) | 2p (-97.1/-75.7) |
| N2 | 1060.5 | 0.17 | 2p (-93.7/-78.5) | 2p (-95.2/-79.4) | ||
| N9 | 1291.5 | 0.83 | 1p? | 1p (-83.2) | ||
| N10 | 1318.5 | 0.91 | np | np | ||
| N12 | 1365.5 | 1.04 | 2p (-97.8/-76.1) | 1p (-79.7) | ||
| N13 | 1386.5 | 1.10 | 2p (-94.6/-76.1) | 1p (-79.4) | ||
| N14 | 1424.5 | 1.21 | 2p (-88.2/-75.5) | 1p (-79.0) | ||
| N22 | 1652.5 | 1.86 | 1p (-73.9) | 1p (-75.6) | ||
| N24 | 1716.5 | 2.05 | 2p (-94.3/-76.9) | 1p (-74.1) | ||
| N27 | 1767.5 | 2.19 | 2p (-91.6/-75.0) | 2p (-94.8/-76.0) | ||
| RS Her | 156 | N9 | 1291.5 | 0.95 | 1p (-34.7) | 1p (-33.8) |
| N10 | 1318.5 | 1.07 | 1p (-40.3) | 1p (-34.1) | ||
| N25 | 1737.5 | 2.98 | 2p (-44.0/-26.8) | ap (-44.5/-30.4) | ||
| RU Oph | 142 | N24 | 1716.5 | 0.00 | 1p (+42.0) | 1p (+40.5) |
| N9 | 1291.5 | -- | 1p (-12.2) | 1p (-12.2) | ||
| N10 | 1318.5 | -- | 1p (-12.5) | 1p (-12.4) | ||
| N12 | 1365.5 | -- | 1p (-12.6) | 1p (-12.6) | ||
| N13 | 1386.5 | -- | 1p (-12.4) | 1p (-12.4) | ||
| N23 | 1683.5 | -- | 1p (-12.3) | 1p (-12.3) | ||
| N26 | 1766.5 | -- | 1p (-12.4) | 1p (-12.7) |
| Name | Night | Julian Date | Phase | K0-template | M4-template | |
| ( |
Number | (2450000+) | ||||
| T Her | 120 | N24 | 1716.5 | 0.03 | 2p (-133.4/-115.0) | 1p (-117.9) |
| RY Oph | 119 | N22 | 1652.5 | 0.95 | 2p (-75.9/-54.7) | 1p (-56.6) |
| RT Dra | 195 | N2 | 1060.5 | 0.04 | 2p? | 1p (-99.8) |
| N3 | 1085.5 | 0.13 | np | 1p (-101.5) | ||
| N4 | 1093.5 | 0.27 | np | ap (-111.8/-100.6) | ||
| N5 | 1171.5 | 0.44 | np | np | ||
| N9 | 1291.5 | 0.87 | 1p (-106.3) | 1p (-104.4) | ||
| N10 | 1318.5 | 0.96 | 1p (-108.8) | 1p (-103.8) | ||
| N12 | 1365.5 | 1.13 | np | 1p (-104.0) | ||
| N13 | 1386.5 | 1.21 | np | 1p (-103.7) | ||
| N14 | 1424.5 | 1.34 | np | 1p (-105.5) | ||
| N15 | 1450.5 | 1.44 | np | 1p (-106.2) | ||
| N22 | 1652.5 | 2.16 | np | 1p (-100.0) | ||
| N23 | 1683.5 | 2.27 | np | 2p (-112.6/-101.9) | ||
| N24 | 1716.5 | 2.39 | np | 1p (-109.4) | ||
| N26 | 1766.5 | 2.57 | np | 1p (-107.4) | ||
| SV Her | 178 | N27 | 1767.5 | 0.94 | 1p (-13.0) | 1p (-13.9) |
| X Oph | 216 | N13 | 1386.5 | 0.90 | 1p (-73.2) | 1p (-71.4) |
| N14 | 1424.5 | 1.02 | 1p (-72.8) | 1p (-70.8) | ||
| N15 | 1450.5 | 1.09 | 1p (-73.1) | 1p (-70.1) | ||
| N26 | 1766.5 | 2.06 | 1p (-74.1) | 1p (-75.2) | ||
| WZ Lyr | 429 | N24 | 1716.5 | 0.97 | 1p? | 1p (+1.7) |
| N26 | 1766.5 | 1.10 | 1p? | 1p (+1.4) | ||
| RU Lyr | 258 | N27 | 1767.5 | 0.98 | 1p? | 1p (-3.3) |
| W Aql | 242 | N23 | 1683.5 | 0.97 | 2p (-53.5/-27.4) | 1p (-23.4) |
| RT Cyg | 130 | N1 | 1031.5 | 0.95 | 2p (-132.5/-110.1) | 1p (-111.4) |
| N2 | 1060.5 | 1.10 | 2p (-130.7/-111.0) | 2p (-134.9/-111.6) | ||
| N3 | 1085.5 | 1.23 | ap (-122.5/-110.3) | 1p (-112.5) | ||
| N12 | 1365.5 | 2.70 | np | np | ||
| N13 | 1386.5 | 2.81 | 1p (-113.0) | 1p (-114.6) | ||
| N14 | 1424.5 | 3.01 | 2p (-130.2/-110.4) | 1p (-112.0) | ||
| N15 | 1450.5 | 3.15 | 2p (-128.5/-111.1) | 2p (-130.7/-112.7) | ||
| N9 | 1291.5 | -- | 1p (-3.1) | 1p (-2.8) | ||
| N23 | 1683.5 | -- | 1p (-3.1) | 1p (-2.9) | ||
| N26 | 1766.5 | -- | 1p (-3.2) | 1p (-3.3) | ||
| 273 | N1 | 1031.5 | 0.76 | np | 1p (-7.1) | |
| N2 | 1060.5 | 0.83 | np | 1p (-5.5) | ||
| N3 | 1085.5 | 0.89 | 1p (-5.1) | 1p (-5.3) | ||
| N4 | 1093.5 | 0.99 | 1p (-5.1) | 1p (-5.7) | ||
| N14 | 1424.5 | 1.73 | np | 1p (-5.5) | ||
| N15 | 1450.5 | 1.79 | np | 1p (-5.0) | ||
| Z Cyg | 189 | N26 | 1766.5 | 0.03 | 2p (-179.4/-160.5) | 1p (-160.9) |
| S Aql | N27 | 1767.5 | 0.95 | ap (-114.7/-100.6) | 1p (-103.2) | |
| Z Aql | 109 | N23 | 1683.5 | 0.08 | 2p (-16.5/+2.4) | 1p (-3.3) |
| WX Cyg | N3 | 1085.5 | 0.96 | 2p (+30.6/+47.6) | np | |
| N4 | 1093.5 | 1.06 | 2p (+25.8/+45.4) | np | ||
| T Cep | 238 | N1 | 1031.5 | 0.23 | 2p? | 1p (-10.9) |
| N2 | 1060.5 | 0.31 | np | 1p (-10.9) | ||
| N12 | 1365.5 | 1.09 | 1p? | 1p (-11.3) | ||
| N14 | 1424.5 | 1.25 | np | 1p (-11.1) | ||
| N23 | 1683.5 | 1.91 | np | 1p (-14.9) | ||
| N27 | 1767.5 | 2.13 | 1p (-15.8) | 1p (-13.9) | ||
| RR Aqr | 127 | N27 | 1767.5 | 0.04 | 2p (-191.0/-174.4) | 2p (-191.3/-178.2) |
| X Peg | 135 | N23 | 1683.5 | 0.01 | ap (-49.1/-35.5) | 1p (-39.7) |
| SW Peg | 222 | N3 | 1085.5 | 0.96 | 1p (-3.8) | 1p (-4.4) |
| N15 | 1450.5 | 1.88 | np | 1p (-4.2) | ||
| AX Cep | N2 | 1060.5 | 0.19: | ap (-5.3/+7.5) | np | |
| N3 | 1085.5 | 0.25: | 1p (-2.1) | np | ||
| N4 | 1093.5 | 0.35: | 1p (-1.0) | np | ||
| N5 | 1171.5 | 0.47: | 1p (+1.6) | np | ||
| N7 | 1233.5 | 0.63: | 1p (+6.7) | np | ||
| N13 | 1386.5 | 1.01: | 2p (-7.2/+7.6) | np | ||
| N14 | 1424.5 | 1.11: | ap (-6.4/+6.3) | np | ||
| N15 | 1450.5 | 1.17: | 1p (-3.7) | np | ||
| N17 | 1529.5 | 1.37: | 1p (-1.6) | np | ||
| N18 | 1554.5 | 1.44: | 1p (+0.0) | np | ||
| N26 | 1766.5 | 1.97: | 2p (-9.9/+7.6) | np | ||
| S Cep | N1 | 1031.5 | 0.89 | 2p (-38.5/-18.2) | np | |
| N2 | 1060.5 | 0.95 | 2p (-37.2/-18.5) | np |
| Name | Night | Julian Date | Phase | K0-template | M4-template | |
| ( |
Number | (2450000+) | ||||
| N3 | 1085.5 | 1.00 | 2p (-36.0/-18.7) | np | ||
| N4 | 1093.5 | 1.08 | 2p (-33.7/-18.6) | np | ||
| N7 | 1233.5 | 1.30 | 1p (-27.0) | np | ||
| N12 | 1365.5 | 1.58 | 1p (-22.0) | np | ||
| N13 | 1386.5 | 1.62 | 1p (-21.1) | np | ||
| N14 | 1424.5 | 1.70 | 1p (-20.7) | np | ||
| N15 | 1450.5 | 1.75 | 1p (-20.7) | np | ||
| N17 | 1529.5 | 1.91 | 2p (-39.0/-20.0) | np | ||
| N18 | 1554.5 | 1.96 | 2p (-39.0/-20.4) | np | ||
| N26 | 1766.5 | 2.40 | 1p (-26.3) | np | ||
| RV Peg | 268 | N27 | 1767.5 | 0.97 | 1p (-32.4) | 1p (-32.5) |
| AR Cep | N1 | 1031.5 | -- | 1p (-16.5) | 1p (-16.3) | |
| N4 | 1093.5 | -- | 1p (-16.0) | 1p (-16.1) | ||
| R Peg | 261 | N2 | 1060.5 | 0.97 | 1p (+20.7) | 1p (+21.7) |
| N3 | 1085.5 | 1.03 | 1p (+20.2) | 1p (+21.9) | ||
| N15 | 1450.5 | 2.00 | 1p? | 1p (+21.5) | ||
| N17 | 1529.5 | 2.21 | np | 1p (+21.8) | ||
| W Peg | 247 | N2 | 1060.5 | 0.02 | 1p? | 1p (-19.5) |
| N3 | 1085.5 | 0.10 | 2p? | 1p (-18.4) | ||
| N13 | 1386.5 | 0.97 | np | 1p (-25.0) | ||
| N15 | 145022.5 | 1.15 | np | 1p (-22.5) | ||
| N27 | 1767.5 | 2.07 | 2p? | 1p (-18.1) | ||
| S Peg | 212 | N2 | 1060.5 | 0.98 | 1p? | 1p (+5.3) |
| N3 | 1085.5 | 1.06 | 1p? | 1p (+6.0) | ||
| N13 | 1386.5 | 2.00 | 1p? | 1p (+4.8) | ||
| RY Cep | 86 | N2 | 1060.5 | 0.60: | 1p (-231.7) | 1p (-233.9) |
| N3 | 1085.5 | 0.77: | 1p (-235.1) | 1p (-230.8) | ||
| N4 | 1093.5 | 1.03: | 1p (-245.1) | 2p (-249.5/-229.3) | ||
| N7 | 1233.5 | 1.76: | 1p (-234.2) | 1p (-234.3) | ||
| N13 | 1386.5 | 2.79: | ap (-234.9/-222.2) | 1p (-235.6) | ||
| N15 | 1450.5 | 3.22: | 1p (-241.5) | ap (-244.5/-231.9) | ||
| N17 | 1529.5 | 3.75: | 1p (-230.8) | 1p (-232.6) | ||
| N18 | 1554.5 | 3.92: | 2p (-242.9/-226.6) | 1p (-229.6) | ||
| N27 | 1767.5 | 5.35: | 1p (-239.2) | 2p (-246.1/-234.0) | ||
| ST And | N4 | 1093.5 | 0.99 | 2p (+27.5/+43.1) | np | |
| N15 | 1450.5 | 1.98 | ap (+28.7/+43.5) | np | ||
| N17 | 1529.5 | 2.22 | ap (+25.0/+33.8) | np | ||
| N18 | 1554.5 | 2.30 | 2p (+27.1/+35.9) | np | ||
| N26 | 1766.5 | 2.95 | 1p (+37.2) | np | ||
| R Cas | 282 | N4 | 1093.5 | 0.41 | np | 1p? |
| N13 | 1386.5 | 1.02 | 1p? | 1p (+22.7) | ||
| N17 | 1529.5 | 1.35 | np | 1p (+20.1) | ||
| N26 | 1766.5 | 1.90 | 1p (+21.3) | 1p (+21.4) |