We have also compared the model stellar filter radii
![]() as predicted by each model-phase combination m with our measured angular stellar filter radii
as predicted by each model-phase combination m with our measured angular stellar filter radii
![]() by comparing the observed and model diameter ratios at
different wavelengths (filter f: 656/10, 673/8, 699/6, 754/6, 781/14 and 1045/9).
By confronting a large variety of Mira models
with the here presented narrow-bandpass observations, we may test
how sensitively monochromatic radius measurements probe model structures and
whether they are indeed reliable tools of Mira diagnostics.
Since different models predict, at different phases, both different stellar filter radii
by comparing the observed and model diameter ratios at
different wavelengths (filter f: 656/10, 673/8, 699/6, 754/6, 781/14 and 1045/9).
By confronting a large variety of Mira models
with the here presented narrow-bandpass observations, we may test
how sensitively monochromatic radius measurements probe model structures and
whether they are indeed reliable tools of Mira diagnostics.
Since different models predict, at different phases, both different stellar filter radii ![]() and different filter CLV curves, we expect better agreement between
model-predicted ratios and observed ratios (based upon the corresponding
model-phase combination of CLV) for models that represent R Leo well and for
model phases that are close to the observed phases than for other models and
phases. Since our five models are taylored to the parameters of o Ceti
which roughly has the same period and luminosity as R Leo (310 days,
and different filter CLV curves, we expect better agreement between
model-predicted ratios and observed ratios (based upon the corresponding
model-phase combination of CLV) for models that represent R Leo well and for
model phases that are close to the observed phases than for other models and
phases. Since our five models are taylored to the parameters of o Ceti
which roughly has the same period and luminosity as R Leo (310 days,
![]() :
derived
from its bolometric flux measured at phase 0.20 close to our observations and its HIPPARCOS parallax),
this comparison should give some hint as to whether any of the models is a fair representation of R Leo.
We must be aware, however,
that model
phases are close to but not identical with observed phases, and cycle-to-cycle
variations may be substantial (BSW96, HSW98).
:
derived
from its bolometric flux measured at phase 0.20 close to our observations and its HIPPARCOS parallax),
this comparison should give some hint as to whether any of the models is a fair representation of R Leo.
We must be aware, however,
that model
phases are close to but not identical with observed phases, and cycle-to-cycle
variations may be substantial (BSW96, HSW98).
For illustration, Fig. 8 presents
the observed and model ratios ![]() /
/
![]() of the stellar filter radii
of the stellar filter radii ![]() and
and
![]() as a function of wavelength
as a function of wavelength ![]() for all applied model series (D, E, P, M and O)
and phases close to our observations (since nearly all model series consist of
several cycles, a best fit selection was applied).
Figure 9 displays the observed and theoretical
ratios for all
model-phase combinations m and all filter pairs.
Figure 10 presents
the distance Dm between the measured and model
stellar filter radius ratios (between all possible pairs of filters)
for each model-phase combination.
The distance Dm is defined as
for all applied model series (D, E, P, M and O)
and phases close to our observations (since nearly all model series consist of
several cycles, a best fit selection was applied).
Figure 9 displays the observed and theoretical
ratios for all
model-phase combinations m and all filter pairs.
Figure 10 presents
the distance Dm between the measured and model
stellar filter radius ratios (between all possible pairs of filters)
for each model-phase combination.
The distance Dm is defined as
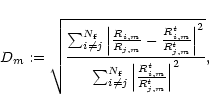 |
(1) |
Inspection of Figs. 8, 9 and 10 shows that from the point of view of diameter
ratios,
some of the model-phase combinations are acceptable as representations
of the here presented observations of R Leo but none is completely satisfactory.
Nearly all models are too compact in the strong TiO absorption band at 673 nm,
i.e. the distance-independent ratio
![]() is too small compared with the observations.
For the model-phase combinations at phases close to the observation, the P model
series which exhibits the most
pronounced atmospheric extension of the BSW96/HSW98 studies
has in most cases (i.e., in 11 out of all 15 filter ratio combinations) model
diameter ratios which are identical (within the error bars) to the measured ones. The order
of ranking
after the P model is: E model (6/15), D model (6/15), M model (3/15) and O model (1/15).
is too small compared with the observations.
For the model-phase combinations at phases close to the observation, the P model
series which exhibits the most
pronounced atmospheric extension of the BSW96/HSW98 studies
has in most cases (i.e., in 11 out of all 15 filter ratio combinations) model
diameter ratios which are identical (within the error bars) to the measured ones. The order
of ranking
after the P model is: E model (6/15), D model (6/15), M model (3/15) and O model (1/15).
Copyright ESO 2001