Detailed investigation of cometary dynamics in the Planetary System gave us 283 original, barycentric orbits of the observed long-period comets with the aphelion distance greater then the PPL. Ten percent of them (28) are hyperbolic, 170 elliptical orbits have $a\leq10\,000$ AU and 85 have $a >10\,000$ AU. Assuming that all those orbits are generally free from significant errors we decided to integrate numerically the past motion of all 255 elliptical comets starting at the moment of crossing the PPL and taking into account the influence of the whole Solar System and the tidal potential of the Galaxy. The aim of this calculation is to look at the past evolution of the cometary orbit. In particular, we are interested in previous aphelion and perihelion distances of all elliptical comets. If we assume that some of the observed long-period comets visited the planetary region as a result of some recent perturbation (for example stellar passage), the aphelion distance might bring the information on the source region of those bodies. On the other hand, for those comets which did not suffer any strong perturbation at the last aphelion (those comets are observable due to the long-term tidal action of the Galaxy), the value of the previous perihelion distance may indicate whether the comet is "physically new'' or has visited the planetary region at least once before the observed return.

During the backward numerical integration of motion we calculated the influence of the Galaxy in an approximate manner, using the model which is widely used in cometary dynamics. The galactic perturbation is restricted here to the tidal action of the galactic disk with the gravitational potential described by the formula derived by Heisler & Tremaine (1986):

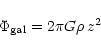
Similar calculations, but for only 48 comets, were performed by Yabushita (1989). Despite the dynamical model differences and a large number of typographical errors in Yabushita's tables, we found a general agreement for the most of his sample of 48 comets, except the cases when we used the updated nominal orbits.

Table 4: The distribution of the previous aphelion distance for all comets believed to be dynamically "new'' in the Oort sense.
Aphelion distane Number of comets

in thousands of AU q>1.5 AU Class 1 All comets

>200 7+0 28+3

200-100 9 14

100-75 7 11

75-50 15 23

50-30 16 24

30-20 6 10

**Table 4:** The distribution of the previous aphelion distance for all comets believed to be dynamically "new'' in the Oort sense.
Aphelion distane	Number of comets
in thousands of AU	q>1.5 AU Class 1	All comets
>200	7+0	28+3
200-100	9	14
100-75	7	11
75-50	15	23
50-30	16	24
30-20	6	10

Table 4 shows the statistics of the previous aphelion distances for all 113 comets "new'' in the Oort sense ( $a >10\,000$ AU) with separate statistics for the "extra quality'' subset. In the first row we present the sum of the number of hyperbolic orbits and of very elongated ellipses. We restricted here our interest to the "new'' comets because for comets with smaller semimajor axes, the influence of the Galaxy is too weak to be observed in orbital elements - they remain constant for one orbital period. This may be clearly seen also in Fig. 1, which additionally is a good illustration of the revised dynamical definitions of "new'' and "old'' comets that we propose below. We recorded here the evolution of orbit in the (q,Q) plane for all 255 elliptical orbits during approximately one orbital period in the past. This plot is constructed during the backward numerical integration as follows: at the beginning we print a small dot, corresponding to the initial data, taken from the barycentric, original orbit set, described in the previous Sect. Next, we print the same small dot at each backward integration step, according to the current values of the osculating perihelion and aphelion distances. Finally, at the end of the integration (at the previous perihelion) we print a big dot.

Figure 1 is divided into three parts, upper, middle and lower, with horizontal dashed lines corresponding to the aphelion distances of 50000 AU and 200000 AU. The vertical dotted line corresponds to the perihelion distance of 15 AU, which we used as the threshold value: only those comets with a greater value of q may be called dynamically "new'', all the others should be considered as dynamically "old'' even if they have a very small value of the original reciprocal semimajor axis. See, for example, the paper by Matese & Whitman (1989) for arguments in support of choosing this particular threshold value.

In the upper part of this plot one can notice rather complicated paths of three comets on very elongated elliptical orbits under a relatively strong galactic perturbation. Those are: C/1896 V1 with the initial aphelion distance of 383952 AU, C/1940 R2 with the initial $Q=2\,954\,501$ AU and C/1993 Q1 having the initial $Q=738\,516$ AU. The initial means here the value at the PPL in the original orbital element set. It should be stressed, that these three comets have small observed perihelion distances (1 AU or less) and we may suspect that their extremely large initial aphelion distances may be a result of nongravitational effects, not included in the orbit determination process.

In the lower part are all the comets that do not significantly change their orbits under the influence of the galactic disk tide during the last orbital period. For the majority of them the final dots are plotted over the starting ones; only for the comets with an initial aphelion distance greater than 20000 AU can one notice small changes in the perihelion distance. All those comets we call dynamically "old'' because during their previous passage near the Sun they deeply penetrated the planetary region.

Only the comets for which the big dots, representing previous perihelion values, lie in the middle part of Fig. 1 and to the right of the vertical dotted line, may be called dynamically "new''. As clearly visible from this plot, they considerably changed their perihelion distance during the last orbital period before being observed, from large values outside the Planetary System to very small ones, close to 1 AU. This means that we should modify the Oort definition of dynamically "new'' comets, changing the threshold value of the reciprocal of the semimajor axis from $1\times10^{-4}$ to $2.5\times10^{-4}$ AU^-1 and excluding those comets with previous perihelion distances smaller than 15 AU.

Table 5: The distribution of the previous perihelion distances for elliptical long-period comets, "new'' in the Oort sense ( $a >10\,000$ AU). The "restricted'' set means comets with observed perihelion distance greater than 1.5 AU and orbit of class 1.
Previous q "restricted'' set all comets

0-2 AU 3 10

2-15 AU 24 31

15-40 AU 6 12

>40 AU 20 32

**Table 5:** The distribution of the previous perihelion distances for elliptical long-period comets, "new'' in the Oort sense ( $a >10\,000$ AU). The "restricted'' set means comets with observed perihelion distance greater than 1.5 AU and orbit of class 1.
Previous q	"restricted'' set	all comets
0-2 AU	3	10
2-15 AU	24	31
15-40 AU	6	12
>40 AU	20	32

Table 5 shows the statistics of the previous perihelion distances. It is clearly visible that 41 comets thus far called dynamically "new'' (and among them 27 comets from the "restricted'' set) have penetrated the planetary system at least once before. According to our modified definition, only 44 comets (26 from the "restricted'' set) can be called dynamically new! If we exclude 3 comets with the extremely elongated (probably erroneously) elliptical orbits mentioned above it appears that exactly $50\%$ of comets called dynamically "new'' are in fact dynamically "old'' and have passed near the Sun at a distance closer than 15 AU. The maximum and minimum heliocentric distances during the last orbit for 41 dynamically "new'' comets according to our definition are shown in Table 6. These are osculating aphelion and perihelion distances, but for two different epochs of osculation (when at aphelion and at perihelion respectively). One can notice that a quarter of them had their previous perihelion passage in the outer planetary region while some of them had large perihelion distances at the previous return.

Table 6: Aphelion (Q) and perihelion (q) distances during last orbit for 41 dynamically "new'' comets according to our modified definition (see text for details).
Comet Q [AU] q [AU]

C/1853 L1 144989 8385

C/1863 T1 131366 5155

C/1902 R1 73187 40

C/1902 X1 75504 138

C/1903 M1 60320 25

C/1906 E1 69869 105

C/1907 E1 78759 70

C/1913 Y1 69017 79

C/1916 G1 114800 758

C/1919 Q2 97494 683

C/1921 E1 104174 1035

C/1922 U1 92708 176

C/1925 W1 83486 140

C/1935 Q1 108284 202

C/1942 C1 124942 1002

C/1944 K2 111507 1566

C/1947 S1 85361 31

C/1947 Y1 72355 82

C/1948 E1 60428 28

C/1948 T1 59020 18

C/1950 K1 53475 15

C/1956 F1-A 113238 1083

C/1962 C1 61046 20

C/1973 E1 115370 669

C/1974 F1 56186 21

C/1974 V1 159240 10180

C/1975 E1 86309 295

C/1976 U1 53793 16

C/1978 A1 58904 45

C/1978 H1 82829 88

C/1978 R3 128057 2537

C/1979 M1 63712 37

C/1984 W2 103493 910

C/1987 W3 68822 58

C/1988 B1 132343 6259

C/1989 X1 63953 48

C/1990 M1 49108 18

C/1991 F2 124304 2761

C/1992 J1 70792 57

C/1997 A1 96745 248

C/1997 BA6 78190 141

**Table 6:** Aphelion (Q) and perihelion (q) distances during last orbit for 41 dynamically "new'' comets according to our modified definition (see text for details).
Comet	Q [AU]	q [AU]
C/1853 L1	144989	8385
C/1863 T1	131366	5155
C/1902 R1	73187	40
C/1902 X1	75504	138
C/1903 M1	60320	25
C/1906 E1	69869	105
C/1907 E1	78759	70
C/1913 Y1	69017	79
C/1916 G1	114800	758
C/1919 Q2	97494	683
C/1921 E1	104174	1035
C/1922 U1	92708	176
C/1925 W1	83486	140
C/1935 Q1	108284	202
C/1942 C1	124942	1002
C/1944 K2	111507	1566
C/1947 S1	85361	31
C/1947 Y1	72355	82
C/1948 E1	60428	28
C/1948 T1	59020	18
C/1950 K1	53475	15
C/1956 F1-A	113238	1083
C/1962 C1	61046	20
C/1973 E1	115370	669
C/1974 F1	56186	21
C/1974 V1	159240	10180
C/1975 E1	86309	295
C/1976 U1	53793	16
C/1978 A1	58904	45
C/1978 H1	82829	88
C/1978 R3	128057	2537
C/1979 M1	63712	37
C/1984 W2	103493	910
C/1987 W3	68822	58
C/1988 B1	132343	6259
C/1989 X1	63953	48
C/1990 M1	49108	18
C/1991 F2	124304	2761
C/1992 J1	70792	57
C/1997 A1	96745	248
C/1997 BA6	78190	141

Table 7: Several examples of large differences between the orbital elements of dynamically "new'' comets, obtained in two different models: without and with the stellar perturbations from the Algol system.
Comet q [AU] e i [ $^{\circ }$ ] $\Delta T$ [ years]

2.1 0.99994820 157.19 -7.88 $\,\times\, 10^{6}$

C/1907 E1 69.6 0.99824162 99.11 -7.78 $\,\times\, 10^{6}$

105.3 0.99718258 118.33 -7.80 $\,\times\, 10^{6}$

3.7 0.99989955 10.94 -7.19 $\,\times\, 10^{6}$

C/1914 M1 4.4 0.99988297 24.55 -7.19 $\,\times\, 10^{6}$

32.0 0.99917286 1.56 -7.20 $\,\times\, 10^{6}$

0.7 0.99997356 145.91 -4.74 $\,\times\, 10^{6}$

C/1954 M2 14.0 0.99950276 101.01 -4.71 $\,\times\, 10^{6}$

16.5 0.99941611 103.01 -4.71 $\,\times\, 10^{6}$

3.2 0.99991611 61.76 -7.34 $\,\times\, 10^{6}$

C/1980 E1 13.3 0.99964770 76.65 -7.30 $\,\times\, 10^{6}$

34.2 0.99911567 33.35 -7.33 $\,\times\, 10^{6}$

4.0 0.99992510 34.56 -1.24 $\,\times\, 10^{7}$

C/1984 W2 909.7 0.98298450 86.85 -1.16 $\,\times\, 10^{7}$

1548.0 0.97085896 83.17 -1.19 $\,\times\, 10^{7}$

1.5 0.99997676 103.03 -1.66 $\,\times\, 10^{7}$

C/1991 F2 2760.6 0.95760870 90.31 -1.53 $\,\times\, 10^{7}$

4154.7 0.93737268 83.30 -1.60 $\,\times\, 10^{7}$

3.4 0.99991292 45.16 -7.85 $\,\times\, 10^{6}$

C/1997 BA6 140.8 0.99643553 83.67 -7.68 $\,\times\, 10^{6}$

238.5 0.99384010 75.58 -7.72 $\,\times\, 10^{6}$

**Table 7:** Several examples of large differences between the orbital elements of dynamically "new'' comets, obtained in two different models: without and with the stellar perturbations from the Algol system.
Comet	q [AU]	e	i [ $^{\circ }$ ]	$\Delta T$ [ years]
	2.1	0.99994820	157.19	-7.88 $\,\times\, 10^{6}$
C/1907 E1	69.6	0.99824162	99.11	-7.78 $\,\times\, 10^{6}$
	105.3	0.99718258	118.33	-7.80 $\,\times\, 10^{6}$
	3.7	0.99989955	10.94	-7.19 $\,\times\, 10^{6}$
C/1914 M1	4.4	0.99988297	24.55	-7.19 $\,\times\, 10^{6}$
	32.0	0.99917286	1.56	-7.20 $\,\times\, 10^{6}$
	0.7	0.99997356	145.91	-4.74 $\,\times\, 10^{6}$
C/1954 M2	14.0	0.99950276	101.01	-4.71 $\,\times\, 10^{6}$
	16.5	0.99941611	103.01	-4.71 $\,\times\, 10^{6}$
	3.2	0.99991611	61.76	-7.34 $\,\times\, 10^{6}$
C/1980 E1	13.3	0.99964770	76.65	-7.30 $\,\times\, 10^{6}$
	34.2	0.99911567	33.35	-7.33 $\,\times\, 10^{6}$
	4.0	0.99992510	34.56	-1.24 $\,\times\, 10^{7}$
C/1984 W2	909.7	0.98298450	86.85	-1.16 $\,\times\, 10^{7}$
	1548.0	0.97085896	83.17	-1.19 $\,\times\, 10^{7}$
	1.5	0.99997676	103.03	-1.66 $\,\times\, 10^{7}$
C/1991 F2	2760.6	0.95760870	90.31	-1.53 $\,\times\, 10^{7}$
	4154.7	0.93737268	83.30	-1.60 $\,\times\, 10^{7}$
	3.4	0.99991292	45.16	-7.85 $\,\times\, 10^{6}$
C/1997 BA6	140.8	0.99643553	83.67	-7.68 $\,\times\, 10^{6}$
	238.5	0.99384010	75.58	-7.72 $\,\times\, 10^{6}$

It should be stressed again that the picture presented so far is obtained by taking into account only the galactic perturbation of the movement of a comet on the elongated elliptic orbit. There is another source of perturbation that is much more difficult to model because of its random nature - namely stellar close passages. On the basis of our knowledge of the solar neighbourhood density of stars and their motions, it is widely believed that several close encounters take place each million years (a detailed discussion may be found for example in: Dybczynski & Kankiewicz 1999; García-Sánchez et al. 1999). A strict analysis of the influence of the neighbour stars on the cometary motion during the last several million years is very difficult because of the incompleteness and inaccuracies in the stellar data at our disposal and is beyond the scope of this article, but to illustrate its importance we present here the results of backward numerical integration of the cometary motion, in which we include (besides the galactic disk tide) the influence of the Algol (HIP 14576) system, which probably has been one of the most prominent perturbers of the Oort cloud comets in the past few million years (García-Sánchez et al. 1999). An additional importance of that system is that we know its spatial position and velocity with great accuracy due to the latest VLBI astrometrical measurements (Lestrade et al. 1999) so the calculation is relatively precise. The total mass of that multiple star system is about 5.8 solar masses, its minimum distance from the Sun was 3 pc and the encounter velocity was as low as 4 kms^-1 (this increases the perturbational effect). Its close passage happened 7 million years ago.

The gravitational influence of that system was included in the equations of cometary motion. Similarly to the previous calculation, all comets with elliptic orbits were integrated numerically one orbital period in the past. For the majority of comets there were no significant differences but some of them exhibit substantial changes in their past orbital motion. The examples of the differences between the two dynamical models mentioned above are given in Table 7. The inclination of the cometary orbit presented in this table is measured with respect to the galactic disk plane. The last column shows the time interval between the observed and previous perihelion passage. For each comet we include three rows containing (from upper to lower) the original orbit at the PPL, orbital elements at the previous perihelion passage under the influence of the galactic disk tide only and the same under both galactic and stellar perturbation due to the Algol system. Note significant differences in the inclination. This is typical because the galactic tide makes this element vary very rapidly near the perihelion (see for example Dybczynski & Pretka 1997), so small changes in the other elements typically result in large inclination changes, but the orientation of the line of apsides remains almost the same. We present here some extreme examples and additionally three comets, which became dynamically "new'' due to the Algol system action. These are C/1914 M1, C/1954 M2 and C/1980 E1. A comparative results for all comets may be found in file: http://main.amu.edu.pl/~dybol/DH/disk-star.wyn. The main conclusion following from this comparison is that stellar perturbations are very important and can change comet orbits, in some cases significantly. We plan to extent our dynamical model for studying cometary past motion by including all stars in the galactic neighbourhood of the Sun with known spatial position and velocity which can noticeably influence the motion of a small body. The first steps in this direction have already been made (Dybczynski & Kankiewicz 1999) and a paper describing results of an extended research in this field is currently in preparation.

4 Going further into the past