With the present STIS spectra of HE 0515-4414 the redshift range
![]() has been covered for the first time at
sufficiently high resolution to undertake a sensitive search for
O VI absorbers. We have detected 6 O VI systems. Two
of them (z = 1.697, 1.736) are either associated with the QSO or
in the proximity zone of the extremely luminous QSO. The system z
= 1.416 is marginal, since only the 1031Å line is detected.
Including the latter, we have 4 detections in the range z = 1.21to 1.67 which yield a number density of O VI absorbers with
has been covered for the first time at
sufficiently high resolution to undertake a sensitive search for
O VI absorbers. We have detected 6 O VI systems. Two
of them (z = 1.697, 1.736) are either associated with the QSO or
in the proximity zone of the extremely luminous QSO. The system z
= 1.416 is marginal, since only the 1031Å line is detected.
Including the latter, we have 4 detections in the range z = 1.21to 1.67 which yield a number density of O VI absorbers with
![]() 25mÅ of
25mÅ of
![]() .
Compared with the findings by Tripp et al. (2000) of
.
Compared with the findings by Tripp et al. (2000) of
![]() at
at
![]() ,
the number density at
,
the number density at
![]() is roughly a factor of 5 lower. Tripp et al.
(2000) compared their finding of a high number density of
weak O VI absorbers (
is roughly a factor of 5 lower. Tripp et al.
(2000) compared their finding of a high number density of
weak O VI absorbers (
![]() 30 mÅ) in
H 1821+643 and PG 0953+415 with other classes of absorbers and
found that the weak O VI number density is more comparable
to that of the low z weak Ly
30 mÅ) in
H 1821+643 and PG 0953+415 with other classes of absorbers and
found that the weak O VI number density is more comparable
to that of the low z weak Ly ![]() absorbers - which have
absorbers - which have
![]() for
for
![]() 50mÅ - than to other types of metal absorbers like Mg II. In
HE 0515-4414 we have at least 42 Ly
50mÅ - than to other types of metal absorbers like Mg II. In
HE 0515-4414 we have at least 42 Ly ![]() systems (the exact
number being unknown due to the line blending problem) with
systems (the exact
number being unknown due to the line blending problem) with
![]() 50mÅ in the range
50mÅ in the range
![]() which yields roughly
which yields roughly
![]()
![]() . Among these, roughly half of them are strong,
saturated Ly
. Among these, roughly half of them are strong,
saturated Ly ![]() lines with a detected Ly
lines with a detected Ly ![]() line.
Again, while our STIS spectrum of HE 0515-4414 confirms the number
density of Ly
line.
Again, while our STIS spectrum of HE 0515-4414 confirms the number
density of Ly ![]() absorbers found previously (see Weymann et al.
1998), the number of O VI absorbers with
absorbers found previously (see Weymann et al.
1998), the number of O VI absorbers with
![]() mÅ is lower than the number of Ly
mÅ is lower than the number of Ly ![]() absorbers
with
absorbers
with
![]() mÅ by a factor of 10. It is
noteworthy that, except the z = 1.674 system, O VI is
detected in lower column density Ly
mÅ by a factor of 10. It is
noteworthy that, except the z = 1.674 system, O VI is
detected in lower column density Ly ![]() absorbers (log
absorbers (log
![]() ). Following the calculations by Tripp et al.
(2000) and earlier work by Storrie-Lombardi et al. (1996) and
Burles & Tytler (1996), the mean cosmological mass-density of
O VI absorbers can be written in units of the critical
density
). Following the calculations by Tripp et al.
(2000) and earlier work by Storrie-Lombardi et al. (1996) and
Burles & Tytler (1996), the mean cosmological mass-density of
O VI absorbers can be written in units of the critical
density
![]() as
as
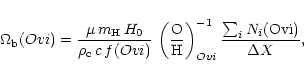 |
(3) |
Over the redshift interval z = 1.21 to z = 1.67 we have
![]() for
q0 = 1/2.
for
q0 = 1/2.
![]() is
is
![]() (Table 1).
Assuming
(Table 1).
Assuming
![]() ,
following Tripp et al. (2000)
and Tripp & Savage (2000), which is close to the maximum for both
collisional ionization and photoionization, we obtain a lower
limit
,
following Tripp et al. (2000)
and Tripp & Savage (2000), which is close to the maximum for both
collisional ionization and photoionization, we obtain a lower
limit
![]() (O VI)
(O VI)
![]()
![]() .
The only reliably
measured heavy element abundances at
.
The only reliably
measured heavy element abundances at
![]() are from
DLAs. Typically the metal abundance (e.g. from Zn) is 1/10 solar
(Pettini et al. 1999; Vladilo et al. 2000). There is, however,
no guarantee that these abundances apply also to the O VI
absorbers among the low column density systems. Assuming 1/10
solar for the oxygen abundance, we have
are from
DLAs. Typically the metal abundance (e.g. from Zn) is 1/10 solar
(Pettini et al. 1999; Vladilo et al. 2000). There is, however,
no guarantee that these abundances apply also to the O VI
absorbers among the low column density systems. Assuming 1/10
solar for the oxygen abundance, we have
![]() .
With the same
assumptions Tripp et al. (2000) derived a value
.
With the same
assumptions Tripp et al. (2000) derived a value
![]() .
Using a somewhat different formalism for
the derivation of
.
Using a somewhat different formalism for
the derivation of
![]() ,
namely Eq. (6) from
Tripp & Savage (2000), we get with the same assumptions
,
namely Eq. (6) from
Tripp & Savage (2000), we get with the same assumptions
![]() (O VI)
(O VI)
![]() .
Both from the number counts of the O VI
systems and the estimate of the mean O VI density the
unavoidable conclusion seems to be that at
.
Both from the number counts of the O VI
systems and the estimate of the mean O VI density the
unavoidable conclusion seems to be that at
![]() ,
the
baryon content of the O VI phase contains a factor of
,
the
baryon content of the O VI phase contains a factor of ![]() less material than at
less material than at
![]() .
.
Copyright ESO 2001