3 Analysis and results

In this section we discuss the applied analysis methods and individual results for the observed comets. After describing the morphology we discuss their magnitudes and make an attempt to estimate the nuclear radii. We also analyze the time series data.

As can be seen in Fig. 1, despite the large solar distances, the observed comets are fairly active. The general appearance is dominated by a small circular coma and a faint, considerably long tail. Although this behaviour is not typical for Short Period Comets, the Long Period Comets display exactly this appearance, keeping the level of activity over a very wide range of distances (Meech 1991). The presented images, that are single exposures, were enhanced nonlinearly to emphasize the faint tail extensions.

Figure 3: The R lightcurves of C/1999 J2 (Skiff) on July 6 and July 9, 2000. The lower panels show the seeing variations.

To derive the physical length of tails one has to estimate their apparent size. The end of the tail was defined where the signal-to-noise ratio of the surface brightness was 2 on the composite images (4 individual exposures co-added). The apparent tails are visible out to 5 $.\mkern-4mu^\prime$8 (C/1999 F2), 5 $.\mkern-4mu^\prime$2 (C/1999 J2), 3 $.\mkern-4mu^\prime$0 (C/1999 N4), 0 $.\mkern-4mu^\prime$8 (C/1999 T2), 0 $.\mkern-4mu^\prime$3 (C/2000 H1) and 5 $.\mkern-4mu^\prime$9 (C/2000 K1).

The measured position angles (PA) are the following (antisolar directions in parentheses): C/1999 F2 - PA 230$^\circ$ (PA 98$^\circ$); C/1999 J2 - PA 18$^\circ$ (PA 80$^\circ$); C/1999 N4 - PA 97$^\circ$ (PA 111$^\circ$); C/1999 T2 - PA 150$^\circ$ (PA 220$^\circ$); C/2000 H1 - PA 90$^\circ$ (PA 76$^\circ$); C/2000 K1 - PA 150$^\circ$ (PA 102$^\circ$). One can find large difference in C/1999 J2 and C/1999 T2 and a smaller one in C/2000 K1, implying a significant amount of tail curvature in these comets. This is supported for C/1999 J2 by the antitail observations by Fukushima et al. (2000) made two months before our observing run. In the meantime the Earth crossed the orbital plane and the tail turned significantly. A colour index of C/1999 J2 also supports a dusty tail (see the photometric analysis) where one may observe apparently long tails if the curvature affects the projection significantly. Neglecting this curvature we calculated the true lengths taking into account the projection effect. The results are $19\times 10^5$ km (C/1999 F2), $8.5\times 10^5$ km (C/1999 J2), $3.2\times 10^5$ km (C/1999 N4), $1.2\times 10^5$ km (C/1999 T2), $0.5\times 10^5$ km (C/2000 H1) and $12\times 10^5$ km (C/2000 K1).

Based on the test images taken previously on non-photometric nights, three of the potential targets were excluded from further observations. The potential targets C/1999 T2 and C/2000 H1 were not really "distant'' object during the observations. Furthermore, C/2000 H1 was quite compact and faint ( $R=19\hbox{$.\!\!^{\rm m}$ }7$, integrated in the innermost 6 $^{\prime\prime}$). C/1999 T2 was bright ( $R=15\hbox{$.\!\!^{\rm m}$ }9$) with a strongly visible coma and 50 $^{\prime\prime}$-long tail. The integrated R magnitude of C/1999 F2 was 19 $.\!\!^{\rm m}$1 in the inner 6 $^{\prime\prime}$, which is fainter than our practical limit. We note the impressive cyrrus-like tail as long as 350 $^{\prime\prime}$.

The surface brightness profiles (e.g. Jewitt & Meech 1987; Lowry et al. 1999) were also calculated to examine the coma regularity. In spherically homogeneous and isotropic cases, the surface brightness (B) profile bears a simple linear relation with a logarithmic derivative of -1. Interaction between overstreaming matter and the radiation pressure modifies this value down to about -2, according to the models by Jewitt & Meech (1987). For our images the profiles were calculated by a model coma along with the nuclear brightness estimation.

The model comae were characterized by two free parameters, namely the slope parameter (logarithmic derivative of the surface brightness) and coma-to-nucleus brightness ratio. The resultant structure is a power-function of the radius with negative exponent, while the nucleus is represented with a delta-function in the center. To simulate the apparent motion and the effect of seeing, the model coma was convolved by the motion and the PSF (Lamy et al. 1998). The latter was determined from individual stellar profiles and its form was a simple Gaussian. We have performed a least-squares analysis, where the finally adopted parameters resulted in an appropriate fit of the observed surface brightness distribution.

The adopted numerical fits of the individual comae are examined in Fig. 2. A comparison of the measurements, the modelled coma components and their sums are presented. The measured brightnesses were averaged in neighbouring rings with a width of $0\hbox{$.\!\!^{\prime\prime}$ }5$. As the background has been taken into account as an additive constant, the effect has been taken into account in this representation too. This allows us to show the photometric data with respect to the real limit of the sky conditions.

Determination of the absolute brightness of the coma allows one to calculate the apparent magnitude of the core, which results in an estimate of the diameter of the solid nucleus. Certainly, as the coma strongly affects the brightness of the nucleus, the apparent brightness of the nucleus can be determined with quite large errors. In the case of the present calculations, the coma contamination was about 1.5-2 magnitudes, therefore, the confidence interval of the estimated diameters may be in the range of half to twice the accepted values.

From the R-band nuclear magnitudes the mean optical cross sections of the nucleii were determined using the equation (Eddington 1910)

$$p_{\rm R} \overline {C} = {2.25 \times 10^{22} \pi R^2 \Delta... ...- \overline{m_R})} \over 10^{\rm -0.4 \alpha \beta} }\nonumber$$

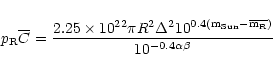
where p_R is the red geometric albedo, $\overline{C}$ is the mean cross section, $m_{\rm Sun}=-27.96$ mag is the R-band magnitude of the Sun and $\overline{m_R}$ is the mean R magnitude of the comet, while $\beta$ is usually assumed to be 0.04 (Luu & Jewitt 1992). An important question is the involved sytematic error, which is very difficult to estimate. The brightness profile of the coma may be distorted by anisotropic substructures (e.g. jets, bright patches) blurred by the seeing. Therefore one can barely calculate the brightness of the nuclei in the case of ground-based observations, and the resulted nuclear diameters are often overestimated (I. Tóth, personal communication).

The remarks on the individual comets are as follows.

Figure 4: The phase diagram of C/1999 J2 (Skiff) (P=1 h).

C/1999 J2 (Skiff)
The object was detected for the first time on CCD frames of the LONEOS-Schmidt (59 cm) telescope on May 13, 1999 for the first time (Skiff et al. 1999). This comet with a discovery brightness of 16 $.\!\!^{\rm m}$0 has the third largest perihelion distance known (7.110 AU, the transit was on April 5, 2000). The apparent total visual brightness was 14 $.\!\!^{\rm m}$5 during the observations, and because of its high declination it was a favourable target for observers in the northern hemisphere. The derived absolute brightness is 3 $.\!\!^{\rm m}$0, which is quite bright compared to other similar comets. The intrinsic peculiarity of this comet was also suggested by the dust antitail reported by Fukushima et al. (2000) in May, 2000.

The observed V-R colour index of the inner coma is $0\hbox{$.\!\!^{\rm m}$ }25\pm0\hbox{$.\!\!^{\rm m}$ }05$. A weak ion tail is barely visible on the direct images, and therefore the relatively bluish colour may be attributed to possible C₂ emission in the V-band. The obtained coma-corrected absolute photometry gave the following mean nuclear brightness: $\langle R \rangle=19\hbox{$.\!\!^{\rm m}$ }9\pm1\hbox{$.\!\!^{\rm m}$ }0$. The coma contamination was estimated to be $87\pm6$% of the total inner intensity (formal error). Assuming 0.04 albedo, the calculated cross section is $p_R C=4\pm3\ {\rm km}^2$ resulting in a nuclear diameter of $10\pm8$ km. This is a quite large value, however, it is simply necessary to support the tremendous activity observed. The logarithmic coma brightness density is linear in the inner 13 $.\!\!^{\prime\prime}$0 with a slope of $-1.6\pm0.1$. This value is significantly larger than the expected one for an isotropic steady-state coma and suggests strong interaction of the outflow and the radiation pressure.

Time-series observations showed that there were rapid small-amplitude variations on a time-scale of an hour, though with small significance. We present the lightcurves in Fig. 3 (the data regard to 1 $.\!\!^{\prime\prime}$3 aperture radius). In order to quantify the cyclic variation, a standard Fourier-analysis was performed. A very short period of $0\hbox{$.\!\!^{\rm h}$ }96\pm0\hbox{$.\!\!^{\rm h}$ }07$ was revealed, the phase diagram is plotted in Fig. 4.

As rotation is the easiest way to explain light variability, we have compared the observed behaviour with the rotational breakup calculations of Davidsson (1999). Accepting rotational variability, the period of rotation is twice the period of the lightcurves. This means approximately 2 hours for the rotational period, which is physically permitted for thopse bodies which are smaller than 4 km in spherical approximation. This does not contradict the estimated diameter of the nucleus. However, other alternative mechanisms cannot be exluded, which are presently unknown. It is worthwhile noting that a similarly fast oscillation has been found for the asteroid 1689 Floris-Jan (Pych 1999), which has long rotational period. The rapid variations were suggested to be caused by secondary rotational effects, though no firm physical explanation was drawn.

Figure 5: The lightcurve of C/1999 N4 (LINEAR) on July 4 and July 6, 2000.

C/1999 N4 (LINEAR)
This retrograde comet was found as an asteroid by the LINEAR project on July 12, 1999 and its unusual motion raised the question of its real nature (Tichy et al. 1999). The discovery was made almost a year before the perihelion at 5.505 AU, therefore, the evolution of this object could be well monitored. The initial brightness of 17 $.\!\!^{\rm m}$5 brightened up to 15 $.\!\!^{\rm m}$0.

Our measurements were taken on 2 nights. On July 4/5 the comet showed a light variation of 0 $.\!\!^{\rm m}$3, the most striking feature of which is the rapid dimming between 23.2 - 01 UT. The lightcurve is presented in Fig. 5. On the second night (July 6) we could detect only an ambiguous variation with an amplitude not exceeding 0 $.\!\!^{\rm m}$08, while a rotation effect would have been expected on this night too. To exclude the correlation with the seeing, the seeing variation is also presented below the lightcurves.

The V-R colour index of the inner coma is 0 $.\!\!^{\rm m}$47$\pm$0 $.\!\!^{\rm m}$05, fairly close to the solar value ((V-R) $_\odot=0\hbox{$.\!\!^{\rm m}$ }36$, Meech et al. 1995). This implies a relatively simple reflection with no emission and little dust. The obtained coma-corrected absolute photometry gave the following mean nuclear brightness: $\langle R \rangle=20\hbox{$.\!\!^{\rm m}$ }6\pm0\hbox{$.\!\!^{\rm m}$ }2$. The coma contamination was estimated to be $90\pm5$% of the total inner intensity (formal error). Assuming 0.04 albedo, the calculated cross section is $p_R C=0.4\pm0.3\ {\rm km}^2$ resulting in a nuclear diameter of $3\pm2$ km. The logarithmic surface brightness profile is the same as for the coma of C/1999 J2: a linear relation in the inner 8 $.\!\!^{\prime\prime}$0 with a slope of $-1.7\pm0.1$.

Figure 6: The lightcurve of C/2000 K1 (LINEAR) on July 4, 2000.

C/2000 K1
The retrograde comet was discovered at a brightness of 18 $.\!\!^{\rm m}$0 by the LINEAR project in May 2000 (Shelly et al. 2000). Further prediscovery images were found on frames from the previous year (Amburgey & Zoltowski 2000). The perihelion passage occurred at 6.276 AU and a visual brightness of 14 $.\!\!^{\rm m}$5.

We have found no significant variation during the observing run (Fig. 6). Unfortunately, we could obtain only the presented 3-hour data series which does not allow any firm conclusion to be drawn. The V-R colour index of the inner coma is $0\hbox{$.\!\!^{\rm m}$ }68\pm0\hbox{$.\!\!^{\rm m}$ }05$, slightly reddish. This means a considerably dusty coma. The obtained coma-corrected absolute photometry gave the following mean nuclear brightness: $\langle R \rangle=19\hbox{$.\!\!^{\rm m}$ }5\pm1\hbox{$.\!\!^{\rm m}$ }0$. The coma contamination was estimated to be $84\pm10$% of the total inner intensity (formal error). Assuming 0.04 albedo, the calculated cross section is $p_R C=5\pm3~{\rm km}^2$ resulting in a nuclear diameter of $11\pm8$ km. As for C/1999 J2, the remarkable tail and coma activity requires a large nucleus. The recorded logarithmic surface brightness profile has a slope of $-1.55\pm0.1$ determined in the inner 14 $.\!\!^{\prime\prime}$0.