in ISO-SWS spectra of oxygen-rich AGB stars
A&A 373, 1125-1138 (2001)
DOI: 10.1051/0004-6361:20010657
D. Fabian1 - Th. Posch2 - H. Mutschke1 - F. Kerschbaum2 - J. Dorschner1
1 - Astrophysikalisches Institut
und Universitätssternwarte,
Schillergässchen 2-3, 07745 Jena, Germany
2 -
Institut für Astronomie, Türkenschanzstrasse 17,
1180 Wein, Austria
Received 16 October 2000 / Accepted 2 May 2001
Abstract
In a previous paper, we have proposed magnesium aluminium spinel
to be the carrier of the 13 and 17 ![]() m band features observed
in the ISO spectra of some red giants. The IR optical properties of spinel
strongly depend on its chemistry and its internal structure.
To study the dependence of spinel's IR-spectra on its aluminium content,
we have synthesized a number of crystals with different Al/Mg-ratios.
Additionally, we performed an annealing experiment to investigate
the phase transition between ordered and partially disordered spinel
taking place at about 1200K.
We derived sets of optical constants of our natural, annealed and
synthetic spinels in order to calculate the absorption efficiencies of
small (sub-
m band features observed
in the ISO spectra of some red giants. The IR optical properties of spinel
strongly depend on its chemistry and its internal structure.
To study the dependence of spinel's IR-spectra on its aluminium content,
we have synthesized a number of crystals with different Al/Mg-ratios.
Additionally, we performed an annealing experiment to investigate
the phase transition between ordered and partially disordered spinel
taking place at about 1200K.
We derived sets of optical constants of our natural, annealed and
synthetic spinels in order to calculate the absorption efficiencies of
small (sub-![]() m-sized) spherical particles. Thereby, it turned out that
natural as well as near-stoichiometric synthetic spinel can indeed
be considered as a suitable candidate for the carrier of the 13
m-sized) spherical particles. Thereby, it turned out that
natural as well as near-stoichiometric synthetic spinel can indeed
be considered as a suitable candidate for the carrier of the 13![]() m
feature observed in the spectra of some oxygen rich circumstellar shells.
To illustrate this, we reinvestigated the mean profile of the residual dust
emission in the 12-18
m
feature observed in the spectra of some oxygen rich circumstellar shells.
To illustrate this, we reinvestigated the mean profile of the residual dust
emission in the 12-18![]() m wavelength range (i.e., in the so-called
trough region between the two silicate bands). The reality of the emission
feature at 16.8
m wavelength range (i.e., in the so-called
trough region between the two silicate bands). The reality of the emission
feature at 16.8![]() m is confirmed by our new investigation.
We demonstrated that it is not an instrumental artifact since it
is not present in ISO spectra of K-stars.
In the course of our laboratory work, we found a third prominent emissivity
maximum of spinel at 32
m is confirmed by our new investigation.
We demonstrated that it is not an instrumental artifact since it
is not present in ISO spectra of K-stars.
In the course of our laboratory work, we found a third prominent emissivity
maximum of spinel at 32![]() m. This feature could also be detected in the spectra
of the brightest 13
m. This feature could also be detected in the spectra
of the brightest 13![]() m band emission sources; we derived its mean band
profile, too.
The new sets of optical constants here presented have been made
available for public access in the electronic database
http://www.astro.uni-jena.de.
m band emission sources; we derived its mean band
profile, too.
The new sets of optical constants here presented have been made
available for public access in the electronic database
http://www.astro.uni-jena.de.
Key words: stars: variables: other - stars: AGB - stars: circumstellar matter - stars: mass-loss - infrared: stars
Since the end of the 1980s, when it was found that IRAS spectra of oxygen rich
AGB stars could not be explained in terms of a silicate dust component only,
refractory oxides have been considered as candidate substances for features in the
mid-IR region, especially in the wavelength range between 10 and 20![]() m.
After the discovery of a previously unknown emission band at 12
m.
After the discovery of a previously unknown emission band at 12![]() m
by Vardya et al. (1986), Onaka et al. (1989) attributed
this feature to
m
by Vardya et al. (1986), Onaka et al. (1989) attributed
this feature to ![]() -Al2O3. Glaccum (1995), analysing
spectra taken with the Kuiper Airborne Observatory, found a 13
-Al2O3. Glaccum (1995), analysing
spectra taken with the Kuiper Airborne Observatory, found a 13![]() m
feature in some M and MS stars and attributed it to "hot sapphire"
(a mineral variety of
m
feature in some M and MS stars and attributed it to "hot sapphire"
(a mineral variety of ![]() -Al2O3 or corundum).
-Al2O3 or corundum).
Begemann et al. (1997), however, have shown that neither
![]() -Al2O3 nor
-Al2O3 nor ![]() -Al2O3 can account
for the 13
-Al2O3 can account
for the 13![]() m emission band, if the simplest assumption concerning
the particle shape and size is made. Only in the rather extreme case of
ellipsoidal particle shapes, they argued, corundum could account for that
feature. As a consequence of this hypothesis, they predicted a second
emission feature at 21
m emission band, if the simplest assumption concerning
the particle shape and size is made. Only in the rather extreme case of
ellipsoidal particle shapes, they argued, corundum could account for that
feature. As a consequence of this hypothesis, they predicted a second
emission feature at 21![]() m, the existence of which could not be
verified up to now on the basis of ISO spectra.
m, the existence of which could not be
verified up to now on the basis of ISO spectra.
A detailed, purely astronomical study of the 13![]() m feature has been
presented by Sloan et al. (1996). They analysed 187 LRS spectra,
finding that 75-90% of all SRb variables, but only 20-25%
of the Miras with oxygen-rich dust show this feature.
Hron et al. (1997) found that the 13
m feature has been
presented by Sloan et al. (1996). They analysed 187 LRS spectra,
finding that 75-90% of all SRb variables, but only 20-25%
of the Miras with oxygen-rich dust show this feature.
Hron et al. (1997) found that the 13![]() m emission peak is
observed within a rather narrow range of stellar photospheric and dust shell
temperatures, which indicates that the formation of its carrier strongly depends
on the physical conditions inside the circumstellar shell.
m emission peak is
observed within a rather narrow range of stellar photospheric and dust shell
temperatures, which indicates that the formation of its carrier strongly depends
on the physical conditions inside the circumstellar shell.
Kozasa & Sogawa (1997, 1998), studying the dust formation from a
theoretical point of view, came to the result that core-mantle-grains composed of
![]() -Al2O3-cores and silicate mantles play an important
role for dust driven stellar winds. As a consequence, they expected the
presence of a dust emission feature between 13 and 14
-Al2O3-cores and silicate mantles play an important
role for dust driven stellar winds. As a consequence, they expected the
presence of a dust emission feature between 13 and 14![]() m in the
spectra of AGB stars with mass loss rates below
m in the
spectra of AGB stars with mass loss rates below
![]() .
Posch et al. (1999, henceforth Paper I) could partly verify this
hypothesis on the basis of the optical constants of corundum and amorphous (Mg, Fe)SiO4.
However, they demonstrated that, if such core-mantle particles were responsible
for an emission feature in the trough region between the two silicate bands,
its position should amount to 14
.
Posch et al. (1999, henceforth Paper I) could partly verify this
hypothesis on the basis of the optical constants of corundum and amorphous (Mg, Fe)SiO4.
However, they demonstrated that, if such core-mantle particles were responsible
for an emission feature in the trough region between the two silicate bands,
its position should amount to 14![]() m, showing a tendency to be shifted
to even larger wavelengths for smaller core volume fractions (i.e., larger
relative strengths of the silicate bands). It was pointed out that neither
this band position nor its tendency to increase for larger relative strengths
of the silicate bands is consistent with ISO observations.
m, showing a tendency to be shifted
to even larger wavelengths for smaller core volume fractions (i.e., larger
relative strengths of the silicate bands). It was pointed out that neither
this band position nor its tendency to increase for larger relative strengths
of the silicate bands is consistent with ISO observations.
Furthermore, Paper I contained a discussion of the IR-optical properties
of the most important modification of TiO2, rutile, and of MgAl2O4,
spinel. The latter was suggested to be the carrier both of the 13![]() m
and of a newly dicovered 16.8
m
and of a newly dicovered 16.8![]() m emission feature (the reality of
which will be confirmed in this paper). Even though the 13
m emission feature (the reality of
which will be confirmed in this paper). Even though the 13![]() m band
is a conspicious emission feature in the spectra of some AGB stars, this
does not imply that its carrier is an abundant dust species in the
circumstellar shells of the respective stars. As Kerschbaum et al. (2000) have shown, only a few percent (1-3%) of the total
amount of dust needs to be composed of spinel in order to account for
the observed band strengths. This is a consequence of the large maximum
intrinsic emissivity of crystalline oxides compared to emissivity of
amorphous silicates.
m band
is a conspicious emission feature in the spectra of some AGB stars, this
does not imply that its carrier is an abundant dust species in the
circumstellar shells of the respective stars. As Kerschbaum et al. (2000) have shown, only a few percent (1-3%) of the total
amount of dust needs to be composed of spinel in order to account for
the observed band strengths. This is a consequence of the large maximum
intrinsic emissivity of crystalline oxides compared to emissivity of
amorphous silicates.
Doubts about the attribution of the 13 ![]() m feature to spinel
were raised by Speck et al. (2000). They claimed that
the dependence of spinel's optical properties on the level of
order of its crystal structure was not taken into account by
Tropf & Thomas (1991), on whose optical constants
Paper I was based. Instead, they attributed the 13
m feature to spinel
were raised by Speck et al. (2000). They claimed that
the dependence of spinel's optical properties on the level of
order of its crystal structure was not taken into account by
Tropf & Thomas (1991), on whose optical constants
Paper I was based. Instead, they attributed the 13 ![]() m
emission to silicon dioxide. This disagreement can, on the basis
of the ISO spectra and laboratory data now available, be settled
rather easily: in this paper, we demonstrate on the one hand that
near-stoichiometric spinel dust forming at high temperature has optical properties
which are in almost perfect correspondence with three emission
features of circumstellar dust (at 13, 17 and 32
m
emission to silicon dioxide. This disagreement can, on the basis
of the ISO spectra and laboratory data now available, be settled
rather easily: in this paper, we demonstrate on the one hand that
near-stoichiometric spinel dust forming at high temperature has optical properties
which are in almost perfect correspondence with three emission
features of circumstellar dust (at 13, 17 and 32 ![]() m).
On the other hand, we can exclude the existence of a 9.25
m).
On the other hand, we can exclude the existence of a 9.25 ![]() m
feature, which should be present in the astronomical spectra if
silicon oxide were the carrier of the 13
m
feature, which should be present in the astronomical spectra if
silicon oxide were the carrier of the 13 ![]() m feature.
m feature.
An ideal method to find out which kind of dust species do condense in circumstellar envelopes is, in principle, the measurement of molecular depletion rates in stellar photospheres or gaseous outflows. Kerschbaum & Olofsson (2001) have recently found first indications of an SiO depletion in the outflows of AGB stars with silicate-rich circumstellar shells. More precisely, they found a decrease in the SiO/CO intensity ratio with the pulsational period of Miras, the latter being a very reliable mass-loss indicator. Unfortunately, it is difficult to apply this method to potential precursor molecules of other dust species (like MgO or AlO), since their abundance is by orders of magnitudes smaller.
It is important to note that refractory oxides have also been found as presolar grains in meteorites. Nittler (1997) reported the identification of a large number of corundum grains, as well as one spinel particle and two grains with compositions intermediate between Al2O3 and spinel, in acid residues of five meteorites. Two grains of a very rare oxide of presolar origin, CaAl12O19 (hibbonite), were identified in an ordinary chondrite by Choi et al. (1999). Choi et al. (1998) came to the remarkable result that presolar corundum and spinel grains show a large range of Al/Mg ratios (2 ...8), interpreting this in terms of a condensation sequence for oxygen-rich circumstellar shells. The starting point of this hypothetical sequence is Al2O3, which, by cooling and back-reacting with Mg atoms and water in the gas phase, would be - partially or wholly - transformed to an Mg-Al-oxide (see also Gail 1998).
In view of the lack of optical constants of spinels with different relative Al and Mg contents, we synthesized a series of Mg-Al-oxides with spinel structure and derived their optical constants. The result of our work is meant to serve not only for the interpretation of currently available ISO spectra, but also as a data basis for future spectroscopy of circumstellar dust.
This paper is structured as follows. In Sect. 2, we first discuss crystallographic properties of natural and synthetic spinels and describe our method of synthesizing the latter; second, we present reflectance spectra of these samples and try to understand them in terms of lattice vibrations; and third, we calculate the optical constants and absorption efficiencies for small particles. In Sect. 3, we compare the results of our laboratory work with new astronomical observations.
The unit cell of natural stoichiometric Mg-Al-spinel consists of 32 oxygen anions,
16 aluminium and 8 magnesium cations. While the trivalent Al cations occupy
a part of the octahedral voids of the cubic close-packed oxygen lattice, the bivalent
Mg ions are situated in tetrahedral interstices. From the examination of synthetic spinels
as well as from studies of presolar grains in meteorites mentioned in the introduction,
we know that the Al/Mg-ratio of these crystals is not restricted to the stoichiometric value
of 2:1. It occurs that in some or in all of a sample's elementary cells, Mg ions are
missing. The tetrahedral sites, therefore, become partly occupied by Al ions,
and vice versa, octahedral sites are partly occupied by Mg ions, but some of the
octahedral sites remain empty. The limiting case with zero Mg content is the cubic
modification of alumina, ![]() -Al2O3, where 3/8 of the
Al ions are located at tetrahedrally coordinated sites
(structural formula [Al]Al
-Al2O3, where 3/8 of the
Al ions are located at tetrahedrally coordinated sites
(structural formula [Al]Al
![]() O4, where []
denotes the tetrahedral sites and
O4, where []
denotes the tetrahedral sites and ![]() the empty octahedral sites).
Although disordering modifies the local lattice symmetry, the overall
cubic crystal symmetry is conserved also for the nonstoichiometric
synthetic compounds. We verified by means of X-ray diffraction
that the nonstoichiometric compounds do not show significant
deviations from the pattern of stoichiometric spinel
- except for a linear increase of the lattice constant with
increasing Mg content (see Viertel & Seifert 1979).
Therefore, it is justified to call the former compounds
nonstoichiometric spinels (and not just Mg-Al-oxides).
Al-deficient samples can also be synthesized and are designated by
the same term.
the empty octahedral sites).
Although disordering modifies the local lattice symmetry, the overall
cubic crystal symmetry is conserved also for the nonstoichiometric
synthetic compounds. We verified by means of X-ray diffraction
that the nonstoichiometric compounds do not show significant
deviations from the pattern of stoichiometric spinel
- except for a linear increase of the lattice constant with
increasing Mg content (see Viertel & Seifert 1979).
Therefore, it is justified to call the former compounds
nonstoichiometric spinels (and not just Mg-Al-oxides).
Al-deficient samples can also be synthesized and are designated by
the same term.
| Designation | sum formula | structural formula |
|
Maxima of R( |
| Mg10 | Mg1.01Al1.99O4 | [Mg0.64Al0.36]Al1.63Mg0.37O4 | 1.96 | 13.6, 18.4, 33.0 |
| Mg09 | Mg0.94Al2.04O4 | [Mg0.59Al0.41]Al1.63Mg
|
2.19 | 13.8, 18.3, 33.0 |
| Mg08 | Mg0.82Al2.12O4 | [Mg0.52Al0.48]Al1.64Mg
|
2.59 | 12.2, 13.8, 18.3, 33.1 |
| Mg07 | Mg0.73Al2.17O4 | [Mg0.46Al0.54]Al1.63Mg
|
3.03 | 12.1, 13.8, 18.3, 33.1 |
| Mg05 | Mg0.53Al2.31O4 | [Mg0.33Al0.67]Al1.64Mg
|
4.35 | 12.0, 14.0, 18.2, 33.1 |
| Mg04 | Mg0.43Al2.38O4 | [Mg0.27Al0.73]Al1.65Mg
|
5.53 | 11.9, 14.1, 18.3, 32.9 |
| Mg10-nat* | Mg1.02Al1.93O4 | [Mg1.02]Al1.93O4 | 1.89 | 13.8, 17.0, 18.6, 32.6 |
| Mg10-ann* | Mg1.02Al1.93O4 | [Mg0.76Al0.24]Al1.69Mg0.26O4 | 1.89 | 13.6, 18.6, 33.2 |
In view of the astrophysical relevance of nonstoichiometric spinels, we have
synthesized a series of them with Al/Mg-ratios ranging from 4.35 to 1.6.
Their designations (Mg10 - Mg05), given in Table 1, correspond to their
respective magnesium content.
Additionally, we examined an even more Al-rich spinel (Al/Mg = 5.53)
produced by the Verneuil method (see, e.g., Strübel 1995).
This sample, henceforth called Mg04, is colourless, has a diameter of about
1 cm and a height of 0.5 cm.
Furthermore, we investigated a natural spinel before ("Mg10-nat'') and after
thermal treatment ("Mg10-ann'' in Table 1). The sample which we used for our
annealing experiment is a dark red, octahedral spinel crystal from Burma with
face diameters exceeding 3 mm. Since the diameter of our spectrometer's aperture
was 2.5 mm, the crystal's size did not affect the spectra. The crystal's
weight, determined after isolating it from the dolomite matrix by means of HCl,
is 219 mg. Its chemical composition, to an accuracy of 10-2, is
Mg1.02Al1.93Si0.03Fe0.01Cr0.01O4.
Since the composition has been determined by EDX - a method which is insensitive
to light elements -, the oxygen content was added to the formula according to stoichiometry.
Although the small (![]() 3%) Si, Fe and Cr impurities may affect the spectra from
the UV to the NIR range, they are practically irrelevant for the resonance bands
in the mid-IR region.
3%) Si, Fe and Cr impurities may affect the spectra from
the UV to the NIR range, they are practically irrelevant for the resonance bands
in the mid-IR region.
To synthesize our samples Mg10 - Mg05, we chose the following method.
MgCO3 and Al(OH)3 powders have been mixed in the corresponding proportions,
in order to get a compound mass of 2 g ![]() 2
2 ![]() 10-3 g.
We did not start with MgO and Al2O3, since these oxides are highly
refractory.
The mixtures have been heated to 1273 K in corundum crucibles and kept
at this temperature for 1h to achieve decomposition to the oxides.
The products of the decomposition have been homogenized in an agate mortar
and were subsequently pressed to pellets. The pellets were transfered to a
tungsten electric-arc furnace with a water-cooled copper baseplate where they were molten in a
1 bar argon atmosphere. In the course of this procedure, we obtained melt-droplets
which were several millimeters in size and colourless, indicating that contamination with
tungsten or copper had not occurred. The samples were exposed to the electric arc
until they were fully molten. This means that the formation temperature was
2323-2408 K (which are the melting points of corundum and spinel,
respectively). According to Andreozzi et al. (2000), in this temperature
range, about 37% of Mg ions occupy octahedral lattice sites, and the corresponding
number of Al ions moves towards tetrahedral interstices. This partial inversion of
the spinel structure occurs rapidly at a high temperature. By contrast, the change
from the disordered to the ordered structure occurs only at low temperatures
and takes a very long time. Therefore, at least in a short-term view, the changes
can be designated as irreversible. The possibility of re-ordering can not be
excluded for long timescales.
The structural formula of stoichiometric spinel synthesized at 2400 K is
[Mg0.63Al0.37]Al1.63Mg0.37O4 (see Table 1).
For Mg-deficient spinels (Mg09 - Mg04), the percentage of Mg ions at
tetrahedral sites remains 37%, but there is not enough magnesium to occupy
all of the octahedral sites: an increasing number of voids arise.
10-3 g.
We did not start with MgO and Al2O3, since these oxides are highly
refractory.
The mixtures have been heated to 1273 K in corundum crucibles and kept
at this temperature for 1h to achieve decomposition to the oxides.
The products of the decomposition have been homogenized in an agate mortar
and were subsequently pressed to pellets. The pellets were transfered to a
tungsten electric-arc furnace with a water-cooled copper baseplate where they were molten in a
1 bar argon atmosphere. In the course of this procedure, we obtained melt-droplets
which were several millimeters in size and colourless, indicating that contamination with
tungsten or copper had not occurred. The samples were exposed to the electric arc
until they were fully molten. This means that the formation temperature was
2323-2408 K (which are the melting points of corundum and spinel,
respectively). According to Andreozzi et al. (2000), in this temperature
range, about 37% of Mg ions occupy octahedral lattice sites, and the corresponding
number of Al ions moves towards tetrahedral interstices. This partial inversion of
the spinel structure occurs rapidly at a high temperature. By contrast, the change
from the disordered to the ordered structure occurs only at low temperatures
and takes a very long time. Therefore, at least in a short-term view, the changes
can be designated as irreversible. The possibility of re-ordering can not be
excluded for long timescales.
The structural formula of stoichiometric spinel synthesized at 2400 K is
[Mg0.63Al0.37]Al1.63Mg0.37O4 (see Table 1).
For Mg-deficient spinels (Mg09 - Mg04), the percentage of Mg ions at
tetrahedral sites remains 37%, but there is not enough magnesium to occupy
all of the octahedral sites: an increasing number of voids arise.
After cooling to subliquidous temperature within a few seconds and subsequent
cooling to room temperature, selected parts of these samples were subjected to an analysis
in a scanning electron microscope equipped with an energy-dispersive X-ray
(EDX) analysis tool. The scanning electron microscope (Leo Stereoscan 440i)
worked at an accelerating voltage of 20 keV and a beam current of 20 pA.
The EDX device was calibrated on a cobalt standard.
Using this configuration, we measured the elemental composition of the products
at five selected spots, 20 ![]() 20
20 ![]() m2 in size.
Neither in the stoichiometric spinel nor in the Mg-deficient samples
did we find any inhomogeneities. The variation in the Al/Mg ratios
from spot to spot did not exceed 1
m2 in size.
Neither in the stoichiometric spinel nor in the Mg-deficient samples
did we find any inhomogeneities. The variation in the Al/Mg ratios
from spot to spot did not exceed 1 ![]() 10-1.
The average Al/Mg ratios are given in Table 1, Col. 4.
The samples showed small deviations from the initial elemental ratios of the powder
mixtures. These differences may either be due to selective MgO evaporation
from the melt or due to water adsorption of the powders.
We also made use of X-ray diffraction to investigate the crystal
structure. Again, it turned out that the samples are crystalline spinels.
None of the samples showed any significant inhomogeneities.
For the spectroscopic measurements, the samples have been embedded in epoxy
resin in order to allow polishing of a plane surface.
10-1.
The average Al/Mg ratios are given in Table 1, Col. 4.
The samples showed small deviations from the initial elemental ratios of the powder
mixtures. These differences may either be due to selective MgO evaporation
from the melt or due to water adsorption of the powders.
We also made use of X-ray diffraction to investigate the crystal
structure. Again, it turned out that the samples are crystalline spinels.
None of the samples showed any significant inhomogeneities.
For the spectroscopic measurements, the samples have been embedded in epoxy
resin in order to allow polishing of a plane surface.
The reflectance spectra of all samples at near-normal incidence have been
measured in an FTIR spectrometer BRUKER 113v in the wavelength range 2-200![]() m
at a resolution of 2cm-1. A gold mirror was used for reference.
The most interesting parts of the reflectance spectra are shown in
Fig. 1. They are characterized by lattice vibrations
causing reflection bands in the wavelength region beyond 10
m
at a resolution of 2cm-1. A gold mirror was used for reference.
The most interesting parts of the reflectance spectra are shown in
Fig. 1. They are characterized by lattice vibrations
causing reflection bands in the wavelength region beyond 10![]() m.
The spectrum of the sample Mg04, which was synthesized by the Verneuil method, is
shown on top of Fig. 1. It fits remarkably well into the series
Mg10 - Mg05.
m.
The spectrum of the sample Mg04, which was synthesized by the Verneuil method, is
shown on top of Fig. 1. It fits remarkably well into the series
Mg10 - Mg05.
While stoichiometric spinels have been studied extensively both experimentally and within the framework of group theory, the situation is much less favourable for the astrophysically relevant nonstoichiometric spinels. We will approach an understanding of their reflectance spectra in two steps: first by summarizing the current knowledge about the "ideal" natural, stoichiometric MgAl2O4, and second by outlining in which way synthetic spinels differ from it. The latter point will involve a description of an annealing experiment carried out with a natural spinel, since it has turned out that annealed natural spinel shows noteworthy structural similarity with synthetic spinels.
![\begin{figure}
\par\includegraphics[width=6.1cm]{fab_f1.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg21.gif) |
Figure 1:
The reflectance spectra of synthetic spinels with
relative Mg contents amounting to 1.01, 0.94, 0.82, 0.73, 0.53
and 0.43 (solid lines, from the bottom to the top). For the sake of clearness,
the reflectances were successively shifted along the y-axis by an amount
of 0.25. In the spectra of the samples with a relative Mg content <0.9
(Mg08 - Mg04), the shoulder at the "blue'' wing of the 14 |
| Open with DEXTER | |
From group theory, four IR active modes were predicted for MgAl2O4(see White & De Angelis 1967; O'Horo et al. 1973). The two
most prominent of them correspond to maxima of the reflectivity around 14 and 18![]() m.
For the sake of brevity, we denominate the 14
m.
For the sake of brevity, we denominate the 14![]() m mode "A'', whereas we
call the 18
m mode "A'', whereas we
call the 18![]() m mode "B'' (see Fig. 1). In powder transmission
measurements, the modes A and B cause minima of
m mode "B'' (see Fig. 1). In powder transmission
measurements, the modes A and B cause minima of
![]() situated at about 15 and
19
situated at about 15 and
19![]() m; in small particle spectra, they correspond to maxima of the absorption
efficiency
m; in small particle spectra, they correspond to maxima of the absorption
efficiency
![]() around 13 and 17
around 13 and 17![]() m (see Sect. 2.3).
Comparing these band positions with spectra of
m (see Sect. 2.3).
Comparing these band positions with spectra of ![]() -Al2O3 and of
MgO, one might be tempted to assume that mode A is due to an Al-O
vibration, while mode B would originate from an Mg-O vibration.
But this is not the case, as Preudhomme & Tarte (1971) have shown
in a careful investigation. They demonstrated that both of the above
mentioned resonances mainly originate from vibrations of the trivalent, octahedral
cation in the spinel lattice, i.e. from an Al-O vibration in the case
of Mg-Al-spinels. In other words, both the frequency of mode A and mode B is practically
independent of the bivalent, tetrahedral cation. If, for example, the Mg ions in
MgAl2O4 are completely replaced by Co ions, the modes A and B do not change
their frequencies significantly.
-Al2O3 and of
MgO, one might be tempted to assume that mode A is due to an Al-O
vibration, while mode B would originate from an Mg-O vibration.
But this is not the case, as Preudhomme & Tarte (1971) have shown
in a careful investigation. They demonstrated that both of the above
mentioned resonances mainly originate from vibrations of the trivalent, octahedral
cation in the spinel lattice, i.e. from an Al-O vibration in the case
of Mg-Al-spinels. In other words, both the frequency of mode A and mode B is practically
independent of the bivalent, tetrahedral cation. If, for example, the Mg ions in
MgAl2O4 are completely replaced by Co ions, the modes A and B do not change
their frequencies significantly.
The remaining two theoretically predicted IR active modes of MgAl2O4
are positioned as follows: one, which we shall call "C'' in Fig. 3,
at the short-wavelength edge of mode B; and one, called "D'', far beyond mode B,
at 33![]() m. According to Preudhomme & Tarte (1971), mode D must be
assigned to an Mg-O vibration, whereas mode C is of a more complex origin.
m. According to Preudhomme & Tarte (1971), mode D must be
assigned to an Mg-O vibration, whereas mode C is of a more complex origin.
Reconsidering Fig. 1 with this background, we notice that no
maximum of
![]() shows up between 14 and 18
shows up between 14 and 18![]() m: mode C is, for a
reason which will be specified later in this section, not visible in any of our
spectra. Mode D shows a tendency to become weaker with decreasing Mg content. (This is
in good agreement with Preudhomme & Tarte's 1971, assignment of this
mode to an Mg-O vibration.) On the other hand, in the spectra of the
Al-rich samples (Mg08 - Mg04), two additional resonance modes become visible at about
12 and 11
m: mode C is, for a
reason which will be specified later in this section, not visible in any of our
spectra. Mode D shows a tendency to become weaker with decreasing Mg content. (This is
in good agreement with Preudhomme & Tarte's 1971, assignment of this
mode to an Mg-O vibration.) On the other hand, in the spectra of the
Al-rich samples (Mg08 - Mg04), two additional resonance modes become visible at about
12 and 11![]() m. For the most Al-rich spinel of our sample, the reflectance maximum
at 12
m. For the most Al-rich spinel of our sample, the reflectance maximum
at 12![]() m becomes as prominent as the one at 14
m becomes as prominent as the one at 14![]() m.
m.
![\begin{figure}
\par\includegraphics[width=8.7cm]{fab_f2.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg25.gif) |
Figure 2:
Comparison between the measured reflectivity of a highly Al-rich synthetic spinel
and the reflectivity of |
| Open with DEXTER | |
In Fig. 2, we compare the reflectance of a selected Al-rich
spinel with the reflectance of ![]() -Al2O3, which, due to its cubic
crystal structure, can be considered as an Mg-free defect spinel. This comparison makes
it probable that the 12
-Al2O3, which, due to its cubic
crystal structure, can be considered as an Mg-free defect spinel. This comparison makes
it probable that the 12![]() m reflectance maximum observed in the spectra
of nonstoichiometric synthetic spinels is in some way related to the
principal peak in the reflectance spectrum of
m reflectance maximum observed in the spectra
of nonstoichiometric synthetic spinels is in some way related to the
principal peak in the reflectance spectrum of ![]() -Al2O3.
It seems that the 12
-Al2O3.
It seems that the 12![]() m resonance mode corresponds to an Al-O vibration
involving tetrahedrally coordinated Al-ions (whereas the group theoretical
calculations mentioned are based on the assumption that all of the Al-ions are
octrahedrally coordinated, which is indeed the case for stoichiometric spinels).
Alluding to the relation between the 12
m resonance mode corresponds to an Al-O vibration
involving tetrahedrally coordinated Al-ions (whereas the group theoretical
calculations mentioned are based on the assumption that all of the Al-ions are
octrahedrally coordinated, which is indeed the case for stoichiometric spinels).
Alluding to the relation between the 12![]() m peak both in the spectra of
Al-rich spinels and of
m peak both in the spectra of
Al-rich spinels and of ![]() -Al2O3, we have called the corresponding
resonance mode "G'' (reminding us of gamma) in Fig. 1.
-Al2O3, we have called the corresponding
resonance mode "G'' (reminding us of gamma) in Fig. 1.
The fact that Al-rich spinels exhibit an additional resonance mode at an even higher frequency than mode A was already pointed out by Hafner & Laves (1961). However, these authors focused on powder transmission measurements, whereas in the context of astrophysics, optical constants and absorption cross sections are desirable (see Sect. 2.3).
Independently from Hafner's & Laves' work, Chihara et al. (2000)
also report the observation of an additional reflectance maximum of an Al-rich
synthetic spinel at a wavelength of 11.9![]() m. Of course, this reflectance maximum corresponds
to the mode that we call G. There is another respect in which the results of Chihara
et al. (2000) are remarkable: for their Al-rich spinel, they additionally
find a resonance at 11.2
m. Of course, this reflectance maximum corresponds
to the mode that we call G. There is another respect in which the results of Chihara
et al. (2000) are remarkable: for their Al-rich spinel, they additionally
find a resonance at 11.2![]() m. On the basis of our sample, we came to the same
result. Due to the fact that we systematically synthesized spinels with a wide range of
Al/Mg-ratios, we recognized that the 11.2
m. On the basis of our sample, we came to the same
result. Due to the fact that we systematically synthesized spinels with a wide range of
Al/Mg-ratios, we recognized that the 11.2![]() m resonance - which appears as a
shoulder (S) of the G band - becomes stronger when the Al/Mg-ratio increases
and more Al-ions occupy tetrahedral interstices of the anion lattice (see again
Fig. 1).
m resonance - which appears as a
shoulder (S) of the G band - becomes stronger when the Al/Mg-ratio increases
and more Al-ions occupy tetrahedral interstices of the anion lattice (see again
Fig. 1).
We shall now address the question why we do not, in any of the spectra shown in
Fig. 1, see any trace of the mode C, which is supposed to produce
a maximum of
![]() near 17
near 17![]() m. This problem will turn out to be
identical with the question of how synthetic spinels, even if stoichiometric
like our Mg10, differ from natural ones in their spectra and in their internal
structure.
m. This problem will turn out to be
identical with the question of how synthetic spinels, even if stoichiometric
like our Mg10, differ from natural ones in their spectra and in their internal
structure.
Having learned from Hafner & Laves (1961) that both synthetic and annealed natural spinels are characterized by a disordered cation distribution, we carried out an annealing experiment with the natural spinel from Burma described in Sect. 2.1. After measuring the spectrum of the unannealed crystal with our Bruker 113v FTIR spectrometer, we annealed the sample for 1h at 1223 K, let it cool down to room temperature and repeated the spectroscopic measurement. The result of this experiment is shown in Fig. 3.
![\begin{figure}
\par\includegraphics[width=5.5cm]{fab_f3.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg26.gif) |
Figure 3:
The IR reflectivity of a near-stoichiometric natural spinel
before and after annealing. Note the presence of a reflectance maximum
labeled "C'' at 17 |
| Open with DEXTER | |
It can be clearly seen that
a) resonance mode A is slightly sharper before the annealing
than afterwards (to verify this, look at the minimum of
![]() at about 16
at about 16![]() m);
m);
b) mode C is only visible as a weak shoulder of mode B in the spectra of
annealed and synthetic spinels;
c) mode D has also become weaker after annealing, and it is weak, too,
in synthetic spinels.
The reason for these effects is an irreversible structural change occuring when spinel is exposed to temperatures above 1200 K. Natural spinel crystals which have not been heated show a well ordered distribution of the Mg and Al cations among the tetrahedrally and octahedrally coordinated voids of the anion lattice, as it was described at the beginning of the Sect. 2.1. Both annealed and synthetic crystals, by contrast, have a disordered cation distribution. This heat-induced disorder involves a partial transition of Al ions to tetrahedral sites and of Mg ions to octahedral sites.
The maximum reflectance values which have recently been presented by Chihara et al. (2000) are systematically higher (by about 10%) than ours. In view of this discrepancy, we checked the absolute accuracy of our reflection measurements by means of a polished bulk silicon standard. However, this did not change our results.
If spinel does indeed condense in circumstellar envelopes, one would expect it to be characterized rather by the disordered lattice structure of annealed (or synthetic) spinel than by that of the natural mineral. On the one hand, this becomes clear from the consideration of condensation as a non-equilibrium process. On the other hand, it is a plausible consequence of spinel's high formation temperature (about 1300K, according to Sedlmayr & Krüger 1997, Fig. 8) and of the short-term irreversibility of the strucural change discussed above. And indeed, we shall see in Sect. 3 that small particle spectra of annealed natural spinel are in good agreement with the dust emission profile derived from ISO spectra.
In Paper I, we used the optical constants published by Tropf &
Thomas (1991), which have recently been critizised by
Speck et al. (2000) as "moot'' because of the former
authors' failure to discuss the effects of nonstoichiometry and
of disordered lattice structure. Having extensively studied the
impact of these effects on spinel's IR reflectance spectra,
we are now in the position
(i) to present reliable optical constants of spinels for a wide
range of Al/Mg-ratios as well as for different degrees of ordering,
and to derive small-particle spectra from them;
(ii) to state that Tropf & Thomas' data represent an acceptable
data set for stoichiometric synthetic spinels; this data set
turns out to be a special case of our much larger one,
but is not criticable as such.
To derive the optical constants
![]() and
and
![]() from the
reflectance spectra, we relied on the classical Lorentz oscillator model,
according to which the dielectric function
from the
reflectance spectra, we relied on the classical Lorentz oscillator model,
according to which the dielectric function
![]() is given by:
is given by:
Sample |
Mode | TOj | ||
| (cm-1) | (cm-1) | (cm-1) | ||
| Mg10 | D | 307.5 | 163.6 | 21.8 |
| 403.0 | 300.5 | 100.8 | ||
| 481.1 | 514.4 | 46.2 | ||
| 505.5 | 694.7 | 51.2 | ||
| 581.4 | 254.4 | 166.4 | ||
| A | 673.9 | 564.7 | 49.1 | |
| G | 805.3 | 94.3 | 58.7 | |
| S | 876.0 | 2.1 | 47.3 | |
| Mg09 | D | 307.3 | 123.0 | 22.5 |
| 414.9 | 179.6 | 79.2 | ||
| 492.3 | 383.7 | 39.8 | ||
| 517.2 | 764.4 | 61.7 | ||
| 606.3 | 286.8 | 174.6 | ||
| A | 676.7 | 575.2 | 46.2 | |
| G | 794.2 | 191.6 | 96.9 | |
| S | 897.2 | 49.6 | 50.6 | |
| Mg08 | D | 309.1 | 140.5 | 21.0 |
| 445.7 | 510.6 | 126.7 | ||
| 497.0 | 527.6 | 39.4 | ||
| 525.0 | 574.4 | 61.2 | ||
| 620.0 | 274.8 | 173.6 | ||
| A | 673.1 | 555.2 | 55.2 | |
| G | 798.9 | 179.8 | 67.0 | |
| S | 885.0 | 61.9 | 52.9 | |
| Mg07 | D | 309.1 | 141.1 | 29.7 |
| 445.7 | 600.0 | 150.0 | ||
| 500.0 | 370.9 | 41.7 | ||
| 532.0 | 560.0 | 64.9 | ||
| 617.1 | 289.5 | 160.4 | ||
| A | 679.1 | 566.5 | 72.3 | |
| G | 804.0 | 227.5 | 62.0 | |
| S | 885.1 | 110.7 | 55.1 | |
| Mg05 | D | 309.7 | 142.7 | 39.0 |
| 450.0 | 605.0 | 151.9 | ||
| 501.4 | 391.4 | 40.6 | ||
| 531.4 | 564.7 | 69.5 | ||
| 622.0 | 339.9 | 135.7 | ||
| A | 676.0 | 540.1 | 68.9 | |
| G | 804.7 | 271.6 | 58.4 | |
| S | 882.6 | 107.9 | 57.1 | |
| Mg04 | D | 314.9 | 172.9 | 44.0 |
| 422.6 | 563.4 | 139.6 | ||
| 490.3 | 475.4 | 51.2 | ||
| 522.4 | 648.3 | 66.9 | ||
| 628.0 | 434.2 | 104.8 | ||
| A | 672.7 | 463.8 | 67.8 | |
| G | 800.9 | 287.8 | 52.2 | |
| S | 888.4 | 99.8 | 49.8 |
Sample |
Mode | TOj | ||
| (cm-1) | (cm-1) | (cm-1) | ||
| Mg10-nat | D | 308.1 | 151.0 | 6.9 |
| 478.6 | 655.5 | 14.0 | ||
| 492.4 | 660.2 | 30.8 | ||
| C | 577.3 | 132.1 | 11.5 | |
| A | 666.6 | 522.9 | 31.9 | |
| G | 803.6 | 159.7 | 82.5 | |
| Mg10-ann | D | 306.9 | 142.0 | 17.0 |
| 404.7 | 267.3 | 102.9 | ||
| 488.5 | 707.6 | 35.6 | ||
| 511.3 | 471.7 | 32.5 | ||
| C | 575.7 | 261.5 | 163.7 | |
| A | 672.6 | 564.0 | 35.9 | |
| G | 806.8 | 90.1 | 49.1 | |
| S | 872.4 | 2.1 | 49.2 |
![\begin{figure}
\par\includegraphics[width=5.5cm]{fab_f4.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg34.gif) |
Figure 4: The optical constants of four selected spinels, plotted on a log-linear scale. Note the large difference between the optical constants of unannealed natural and annealed spinel. |
| Open with DEXTER | |
Figure 4 is a good illustration of our claim that it makes
a large difference whether one uses the optical constants of unannealed natural
or those of synthetic spinel. Despite the nearly identical chemistry of
the natural sample and the sample "Mg10'', their
![]() and
and
![]() are quite different from each other. This is a consequence of the heat-induced
disorder both in the lattice of synthetic and of annealed spinels.
are quite different from each other. This is a consequence of the heat-induced
disorder both in the lattice of synthetic and of annealed spinels.
From the optical constants, the volume normalized scattering and absorption
cross sections of small spherical dust particles can be calculated. The latter
quantity,
![]() /V, is also called emissivity, since for optically thin
dust shells, it governs the dust emission profile. Recall that in the
Rayleigh-limit (i.e. for particles small compared to the wavelength),
the emissivity of spheres can be derived from the complex refractive index
m = n + ik by the simple relation:
/V, is also called emissivity, since for optically thin
dust shells, it governs the dust emission profile. Recall that in the
Rayleigh-limit (i.e. for particles small compared to the wavelength),
the emissivity of spheres can be derived from the complex refractive index
m = n + ik by the simple relation:
![\begin{figure}
\par\includegraphics[width=5.5cm]{fab_f5.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg37.gif) |
Figure 5:
Upper panel: the mid-IR emissivity of the synthetic spinels
Mg04, Mg05, Mg07, Mg08, Mg09 and Mg10 in the wavelength range from
10-20 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{fab_f6.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg38.gif) |
Figure 6:
The IR emissivity of an unannealed natural, an annealed
and an Al-rich synthetic spinel (Mg05), shown on a log-log scale. Note the
peak around 32 |
| Open with DEXTER | |
Assuming the circumstellar spinel particles to be sub-![]() m-sized
and (nearly) spherical, their emissivity profile can with sufficient
precision be calculated with this equation. The result is shown in
Figs. 5, 6 and - as far as the band positions are concerned -
in Table 3. There is one respect in which the spectra shown
in these figures differ from all of the previous ones: due to the
factor 6
m-sized
and (nearly) spherical, their emissivity profile can with sufficient
precision be calculated with this equation. The result is shown in
Figs. 5, 6 and - as far as the band positions are concerned -
in Table 3. There is one respect in which the spectra shown
in these figures differ from all of the previous ones: due to the
factor 6![]() /
/![]() occuring at the right-hand-side of Eq. (2),
the values of
occuring at the right-hand-side of Eq. (2),
the values of
![]() strongly decrease towards longer wavelengths (which
is not the case for the reflectance, nor for the optical constants). Therefore,
spinel's resonance mode "B'' produces a weaker peak than resonance mode
"A'' - even though the intrinsic oscillator strength of mode B
is larger than that of mode A. On the other hand, the high-energy
(short wavelength) resonance mode "G'' - which we have seen to be characteristic
of Al-rich spinels - is very prominent in the small particle spectra.
For Mg04, Mg05 and Mg07, the 12
strongly decrease towards longer wavelengths (which
is not the case for the reflectance, nor for the optical constants). Therefore,
spinel's resonance mode "B'' produces a weaker peak than resonance mode
"A'' - even though the intrinsic oscillator strength of mode B
is larger than that of mode A. On the other hand, the high-energy
(short wavelength) resonance mode "G'' - which we have seen to be characteristic
of Al-rich spinels - is very prominent in the small particle spectra.
For Mg04, Mg05 and Mg07, the 12![]() m
m
![]() -peak corresponding to
this mode is as high as the 13
-peak corresponding to
this mode is as high as the 13![]() m peak, or even higher. For the
stoichiometric sample Mg10, the 13
m peak, or even higher. For the
stoichiometric sample Mg10, the 13![]() m emissivity maximum is the clearly
dominant spectral feature, whereas a secondary peak at 17
m emissivity maximum is the clearly
dominant spectral feature, whereas a secondary peak at 17![]() m
(corresponding, of course, to the vibrational mode B) is less prominent
by a factor of four. As we shall see in Sect. 3.1, the
emissivity of a stoichiometric (or near-stoichiometric) spinel is rather
well consistent with the emissivity of the carrier of the astronomical
13
m
(corresponding, of course, to the vibrational mode B) is less prominent
by a factor of four. As we shall see in Sect. 3.1, the
emissivity of a stoichiometric (or near-stoichiometric) spinel is rather
well consistent with the emissivity of the carrier of the astronomical
13![]() m feature.
m feature.
The 32![]() m peak in the small particle spectra, which corresponds to
resonance mode "D'', is only visible in a logarithmic plot. Figure 6
shows that it is very conspicious for our natural
spinel, somewhat weaker for the annealed one, and very weak for an
Al-rich crystal like Mg05. We will come back later to this very
interesting feature in Sect. 3.2
m peak in the small particle spectra, which corresponds to
resonance mode "D'', is only visible in a logarithmic plot. Figure 6
shows that it is very conspicious for our natural
spinel, somewhat weaker for the annealed one, and very weak for an
Al-rich crystal like Mg05. We will come back later to this very
interesting feature in Sect. 3.2
| Designation | sum formula | Maxima of
|
| Mg10-nat | Mg1.02Al1.93O4 | 13.3, 16.8, 17.5, 32.2 |
| Mg10-ann | Mg1.02Al1.93O4 | 13.1, 17.0, 32.3 |
| Mg10 | Mg1.01Al1.99O4 | 13.0, 16.9, 32.0 |
| Mg09 | Mg0.94Al2.04O4 | 13.0, 16.8, 32.3 |
| Mg08 | Mg0.82Al2.12O4 | 13.1, 16.8, 32.0 |
| Mg07 | Mg0.73Al2.17O4 | 12.1, 13.2, 16.8, 31.8 |
| Mg05 | Mg0.53Al2.31O4 | 12.0, 13.3, 16.8, 31.6 |
| Mg04 | Mg0.43Al2.38O4 | 11.9, 13.3, 16.8, 30.7 |
Considering the lower panel of Fig. 5, we find again that the
small particle spectrum of spheres, in its overall shape, has become smoother after
annealing. (This was even more evident from the reflectance measurements of
Fig. 3.) The double-peak at 17![]() m has disappeared after
the thermal treatment of the crystal. The 13
m has disappeared after
the thermal treatment of the crystal. The 13![]() m emissivity maximum has
broadened and shifted towards 13.1
m emissivity maximum has
broadened and shifted towards 13.1![]() m.
m.
In the present context, we restricted the discussion to the case of spherical
particles, since we know from the astronomical spectra that the full width at
half maximum (FWHM) of the 13 ![]() m feature is only 0.6
m feature is only 0.6 ![]() m on the
average (see Sect. 3).
As we have demonstrated in Paper I (Fig. 6), for a continuous distribution
of ellipsoids (CDE), the width of the 13
m on the
average (see Sect. 3).
As we have demonstrated in Paper I (Fig. 6), for a continuous distribution
of ellipsoids (CDE), the width of the 13 ![]() m feature amounts to 2
m feature amounts to 2![]() m.
Powder transmission spectra also show very broad absorption features - similar
to the case of a CDE - and will therefore not be used for the comparison with
the spectra of circumstellar dust shells.
Of course, we cannot exclude that irregularly shaped spinel particles
also evolve in oxygen-rich circumstellar shells. But apparently, if such
a population of irregularly shaped grains is present at all, it does not
dominate the spectral energy distribution.
m.
Powder transmission spectra also show very broad absorption features - similar
to the case of a CDE - and will therefore not be used for the comparison with
the spectra of circumstellar dust shells.
Of course, we cannot exclude that irregularly shaped spinel particles
also evolve in oxygen-rich circumstellar shells. But apparently, if such
a population of irregularly shaped grains is present at all, it does not
dominate the spectral energy distribution.
![\begin{figure}
\par\includegraphics[width=10cm]{fab_f7.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg40.gif) |
Figure 7:
The reduced ISO-SWS01-spectra in the 8-18 |
| Open with DEXTER | |
In Paper I, we used 11 ISO-SWS-spectra of semiregular variables to study
the dust emission in the trough region between the two silicate bands
(i.e., in the wavelength region 12-17![]() m). We focussed on
the 13
m). We focussed on
the 13![]() m band profile - arriving at a mean band position of 13.0
m band profile - arriving at a mean band position of 13.0![]() m
and an average FWHM of 0.6
m
and an average FWHM of 0.6![]() m - and found additional minor emission
features at 15.8 and 16.8
m - and found additional minor emission
features at 15.8 and 16.8![]() m.
m.
Apart from presenting optical constants of substances that could contribute
to 12-17![]() m dust emission, our present aim is to check the validity
of our above mentioned spectroscopic results on the basis of a larger
data set. For this purpose, we additionally reduced spectra from 2 open time
ISO projects (fkerschb.zzagb2pn; jhron.varlpv) and spectra from the ISO
archive by means of the ISO Spectral Analysis Package (ISAP). Figure 7
shows the 8-18
m dust emission, our present aim is to check the validity
of our above mentioned spectroscopic results on the basis of a larger
data set. For this purpose, we additionally reduced spectra from 2 open time
ISO projects (fkerschb.zzagb2pn; jhron.varlpv) and spectra from the ISO
archive by means of the ISO Spectral Analysis Package (ISAP). Figure 7
shows the 8-18![]() m region of these SWS spectra.
The exposure time of the spectra was chosen corresponding to the brightness
of the stars. R Dor, for example, was observed with scanning speed 1, whereas
for the faintest sample star, CE And, speed 4 was used.
m region of these SWS spectra.
The exposure time of the spectra was chosen corresponding to the brightness
of the stars. R Dor, for example, was observed with scanning speed 1, whereas
for the faintest sample star, CE And, speed 4 was used.
While some of the stars (like CE And, W Hya, ![]() Aps, RX Boo and R Cas)
exhibit more or less classic silicate emission, there is also the peculiar case of R Cen.
The position of its maximum dust emission amounts to about 12
Aps, RX Boo and R Cas)
exhibit more or less classic silicate emission, there is also the peculiar case of R Cen.
The position of its maximum dust emission amounts to about 12![]() m. One possible
explanation for this strange spectral shape is that an Al-rich spinel dust (like our Mg07)
is responsible both for the 12 and for the 13
m. One possible
explanation for this strange spectral shape is that an Al-rich spinel dust (like our Mg07)
is responsible both for the 12 and for the 13![]() m emission (see
Fig. 5).
In most of the other ISO spectra, no conspicious 12
m emission (see
Fig. 5).
In most of the other ISO spectra, no conspicious 12![]() m emission feature is
present. In the residual emission profile of Fig. 8, a small
feature is visible at 12
m emission feature is
present. In the residual emission profile of Fig. 8, a small
feature is visible at 12![]() m; but since its strength is not comparable with
the 13
m; but since its strength is not comparable with
the 13![]() m emission, it is compatible only with the emissivity of a
slightly Al-enriched spinel (see the more detailed
discussion below).
m emission, it is compatible only with the emissivity of a
slightly Al-enriched spinel (see the more detailed
discussion below).
It is interesting to note that even for stars with a rather weak 13![]() m feature
like R Cas, the band position is not shifted towards longer wavelengths as
it should be the case if its carrier were core-mantle-particles composed of
corundum and an amorphous silicate (see Paper I, Figs. 10 and 11).
m feature
like R Cas, the band position is not shifted towards longer wavelengths as
it should be the case if its carrier were core-mantle-particles composed of
corundum and an amorphous silicate (see Paper I, Figs. 10 and 11).
For five of our sample stars, Justtanont et al. (1998) have pointed out a correlation
between the 13![]() m band strength and the intensity of the CO2 emission/absorption
lines. This correlation is also evident from Fig. 7.
m band strength and the intensity of the CO2 emission/absorption
lines. This correlation is also evident from Fig. 7.
Table 4 summarizes the basic properties of the sample stars.
The LRS classes listed in Col. 6 originate from the LRS atlas (IRAS Science
Team 1986); 12![]() m flux densities were taken from the ISO
spectra after reducing the spectral resolution to R = 50.
Data on the gas mass-loss were calculated from the IRAS 60
m flux densities were taken from the ISO
spectra after reducing the spectral resolution to R = 50.
Data on the gas mass-loss were calculated from the IRAS 60![]() m
fluxes by means of the method outlined by Kerschbaum & Olofsson
(1999).
m
fluxes by means of the method outlined by Kerschbaum & Olofsson
(1999).
| Name | IRAS Name | Type | Period | Spectrum | LRS | F12 |
|
dM/dt | 13 |
FWHM |
| [d] | [Jy] | [km/s] | [ |
[ |
[ |
|||||
VY Cas |
00484+6238 | SRb | 100 | M6-M7 | 22 | 38 | - |
|
12.9 | 0.6 |
| CE And | 01265+4624 | Lb | - | M2 | 28 | 13 | 12 |
|
13.0 | 0.6 |
| R Dor | 04361-6210 | SRb | 338 | M7 | 1n | 5157 | 6 |
|
13.1 | 0.75 |
| R Hya | 13269-2301 | M | 389 | M6e-M9e | 15 | 1293 | 10 |
|
13.1 | 0.7 |
| W Hya | 13462-2807 | SRa | 361 | M8e-M9e | 02 | 2665 | 8 |
|
13.0 | 0.5 |
| 14003-7633 | SRb | 119 | M3 | 22 | 734 | 6 |
|
13.0 | 0.6 | |
| R Cen | 14129-5940 | M | 546 | M4e-M8e | 22 | 485 | - |
|
13.0 | 0.5 |
| RX Boo | 14219+2555 | SRb | 340 | M7e-M9e | 2n | 895 | 10 |
|
13.0 | 0.6 |
| S Pav | 19510-5919 | SRa | 381 | M7 | 14 | 502 | 9 |
|
13.1 | 0.7 |
| V1943 Sgr | 20038-2722 | Lb | - | M8 | 15 | 359 | 7 |
|
13.0 | 0.7 |
| T Cep | 21088+6817 | M | 388 | M6e | 15 | 753 | 6 |
|
13.1 | 0.7 |
| R Cas | 23558+5106 | M | 430 | M6e-M10e | 24 | 868 | 12 |
|
13.1 | 0.5 |
By the method outlined in Paper I, we derived individual residual
emission profiles in the 12-17![]() m wavelength region. These
were then added up (together with the profiles shown in Paper I)
to derive a mean residual emission profile, now containing
the information from a total of 23 ISO spectra. The result of
this procedure is shown in Fig. 8.
In spite of the fact that we included twelve new ISO spectra here,
the resulting 13
m wavelength region. These
were then added up (together with the profiles shown in Paper I)
to derive a mean residual emission profile, now containing
the information from a total of 23 ISO spectra. The result of
this procedure is shown in Fig. 8.
In spite of the fact that we included twelve new ISO spectra here,
the resulting 13![]() m band profile has remained practically the same
as the one shown in Figs. 3 and 14 of Paper I. The mean band position
is again 13.0
m band profile has remained practically the same
as the one shown in Figs. 3 and 14 of Paper I. The mean band position
is again 13.0![]() m and the average FWHM 0.6
m and the average FWHM 0.6![]() m. Note that also the
existence of a weak feature at 16.8
m. Note that also the
existence of a weak feature at 16.8![]() m is confirmed by our reinvestigation.
m is confirmed by our reinvestigation.
On the basis of the laboratory data presented in Sect. 2, we may now
adress the question which Al/Mg-ratios of spinel are compatible with
the observed dust emission. Comparing Fig. 8 with
Fig. 5, we recognize that the 12-17![]() m emission
profile is not compatible with large Al/Mg ratios.
For Al/Mg-ratios greater than 2.5, the 12
m emission
profile is not compatible with large Al/Mg ratios.
For Al/Mg-ratios greater than 2.5, the 12![]() m peak of
m peak of
![]() becomes comparable in its strength with the 13
becomes comparable in its strength with the 13![]() m
peak, which is definitely not consistent with the astronomical
spectra. For Al/Mg-ratios below 2.19, the 12
m
peak, which is definitely not consistent with the astronomical
spectra. For Al/Mg-ratios below 2.19, the 12![]() m peak
is clearly less conspicious than the one at 13
m peak
is clearly less conspicious than the one at 13![]() m and the
position of the 13
m and the
position of the 13![]() m band agrees rather well with the
peak position observed with ISO. A reasonable overall agreement
can be achieved with the small particle spectrum of our stoichiometric
synthetic sample Mg10 and with that of the annealed natural spinel.
However, the latter, due to its annealing temperature of 1300 K
- which is very close to the temperature for the corundum-spinel
transition according to Gail (1998) -, is more likely to
represent circumstellar spinel dust. (Recall that the synthetic sample
Mg10 was formed at about 2400 K and therefore has a different
degree of disordering than the annealed natural crystal.)
m band agrees rather well with the
peak position observed with ISO. A reasonable overall agreement
can be achieved with the small particle spectrum of our stoichiometric
synthetic sample Mg10 and with that of the annealed natural spinel.
However, the latter, due to its annealing temperature of 1300 K
- which is very close to the temperature for the corundum-spinel
transition according to Gail (1998) -, is more likely to
represent circumstellar spinel dust. (Recall that the synthetic sample
Mg10 was formed at about 2400 K and therefore has a different
degree of disordering than the annealed natural crystal.)
In order to find out whether the 16.8![]() m is real or spurious, we reduced
the spectra of three K-stars:
m is real or spurious, we reduced
the spectra of three K-stars: ![]() Tuc, HR 6705 and HD 149447. If the 16.8
Tuc, HR 6705 and HD 149447. If the 16.8![]() m
were an artifact caused by the ISO-SWS, it should also show up in the spectra of these
stars. This is not the case, though. Only at 16
m
were an artifact caused by the ISO-SWS, it should also show up in the spectra of these
stars. This is not the case, though. Only at 16![]() m do we suspect a spurious feature.
It is also visible in Fig. 8 to the left of the lowest-energy
CO2-line.
m do we suspect a spurious feature.
It is also visible in Fig. 8 to the left of the lowest-energy
CO2-line.
![\begin{figure}
\par\includegraphics[width=8.7cm]{fab_f8.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg49.gif) |
Figure 8:
The average residual emission profile in the 12-18 |
| Open with DEXTER | |
We have seen in Sect. 2.3 that an additional emission band, originating
from an Mg-O-vibration, is expected to show up at 32![]() m. In fact, in those
of our spectra where the signal-to-noise ratio beyond 30
m. In fact, in those
of our spectra where the signal-to-noise ratio beyond 30![]() m is still good,
we do see a feature at this wavelength. Figure 9 shows the ISO spectra
of R Dor, W Hya, R Hya, T Cep, S Pav and
m is still good,
we do see a feature at this wavelength. Figure 9 shows the ISO spectra
of R Dor, W Hya, R Hya, T Cep, S Pav and ![]() Aps in the 10-35
Aps in the 10-35![]() m range
together with the emissivity of annealed natural and stoichiometric synthetic spinel.
All these stars show a rather narrow 32
m range
together with the emissivity of annealed natural and stoichiometric synthetic spinel.
All these stars show a rather narrow 32 ![]() m emission band which seems
to be well correlated in its strength with the 13 and 16.8
m emission band which seems
to be well correlated in its strength with the 13 and 16.8![]() m local
emission intensities. A systematic investigation of this feature is
definitely desirable.
m local
emission intensities. A systematic investigation of this feature is
definitely desirable.
As a first step, we have derived a mean profile of the 32 ![]() m
feature exactly in the same way as for the residual emission in the
12-18
m
feature exactly in the same way as for the residual emission in the
12-18![]() m range, but of course only on the basis of the beforementioned
six high signal-to-noise ISO spectra. The result is shown in Fig. 10,
together with the continuum-subtracted emissivities
of our samples Mg10 and Mg10-ann. Again, the annealed natural spinel
turns out to be quite similar to the feature carrier with respect to
the band position. With respect to the feature width, the agreement
between the ISO data (
m range, but of course only on the basis of the beforementioned
six high signal-to-noise ISO spectra. The result is shown in Fig. 10,
together with the continuum-subtracted emissivities
of our samples Mg10 and Mg10-ann. Again, the annealed natural spinel
turns out to be quite similar to the feature carrier with respect to
the band position. With respect to the feature width, the agreement
between the ISO data (
![]()
![]() 0.5
0.5![]() m) and the
emissivity of annealed spinel (
m) and the
emissivity of annealed spinel (
![]()
![]() 1.5
1.5![]() m)
is not so good. However, it should be taken into account that the
mean band profile shown in Fig. 10 remains to be re-examined
on the basis of a larger number of observations.
m)
is not so good. However, it should be taken into account that the
mean band profile shown in Fig. 10 remains to be re-examined
on the basis of a larger number of observations.
![\begin{figure}
\par\includegraphics[width=9cm]{fab_f9.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg52.gif) |
Figure 9:
Comparison of the ISO-spectra of six bright stars from
our sample with the emissivity of annealed natural and Mg-rich synthetic
spinel in the 7-40 |
| Open with DEXTER | |
Crystalline silicates can be excluded as carrier of this feature
on the basis of laboratory studies performed by Jäger et al. (1998).
In accordance with the result of Jäger et al., Molster et al. (1999)
found silicate features in their spectra of AFGL 4106 at 32.8 and 33.6![]() m,
but none between 31.5 and 32
m,
but none between 31.5 and 32![]() m.
m.
The peaks at 20 and 28 ![]() m which are also present in the
six plotted spectra (the latter also in the residual profile of
Fig. 10), are instrumental artifacts, the former being
probably due to a wrong gradient at the "blue" end of SWS band 3D
(19.4-27.5
m which are also present in the
six plotted spectra (the latter also in the residual profile of
Fig. 10), are instrumental artifacts, the former being
probably due to a wrong gradient at the "blue" end of SWS band 3D
(19.4-27.5![]() m), the latter being due to a red leak in
SWS band 3E (27.4-29.1
m), the latter being due to a red leak in
SWS band 3E (27.4-29.1![]() m).
m).
A puzzling question, which can also provide constraints on the origin of
the 13![]() m feature, is whether there exists a correlation between its
strength and the intensity of the silicate dust emission. Considering Fig. 8 of
Begemann et al. (1997), one will be tempted to answer this question
with a definite "yes". However, we found it necessary to reexamine this point
using the following method. First, we rebinned the ISO spectra to a spectral
resolution of R=50. From these rebinned spectra, we took the flux values F10, F12,
F13 and F14 at 10, 12, 13 and 14.3
m feature, is whether there exists a correlation between its
strength and the intensity of the silicate dust emission. Considering Fig. 8 of
Begemann et al. (1997), one will be tempted to answer this question
with a definite "yes". However, we found it necessary to reexamine this point
using the following method. First, we rebinned the ISO spectra to a spectral
resolution of R=50. From these rebinned spectra, we took the flux values F10, F12,
F13 and F14 at 10, 12, 13 and 14.3![]() m to derive an effective 13
m to derive an effective 13![]() m feature
strength:
m feature
strength:
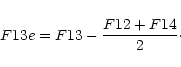 |
(3) |
Altogether, it is rather unlikely that the 13 and the 10![]() m emission
are due to one and the same carrier substance.
m emission
are due to one and the same carrier substance.
![\begin{figure}
\par\includegraphics[width=8.7cm]{fab_f10.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg54.gif) |
Figure 10:
The average residual emission profile in the 26-39 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{fab_f11.ps} \end{figure}](/articles/aa/full/2001/27/aa10357/Timg55.gif) |
Figure 11:
The effective 13 |
| Open with DEXTER | |
We have studied the infrared optical properties of Mg-Al-oxides with spinel structure, highlighting both the effect of annealing natural spinel and the influence of nonstoichiometry on the complex index of refraction.
It was shown that beyond about 1200K, a structural disordering
of the cation distribution of natural spinel takes place, leading
to a significant change in the optical constants. The position
of the 13![]() m band expected to arise from small spherical
spinel particles is shifted to the "blue" by 0.3
m band expected to arise from small spherical
spinel particles is shifted to the "blue" by 0.3![]() m in the
course of annealing. The 17
m in the
course of annealing. The 17![]() m band loses its double-peak
structure.
m band loses its double-peak
structure.
Synthetic aluminium spinels, if stoichiometric, have the same lattice
structure and IR-optical properties as annealed natural ones do. However,
for nonstoichiometric, Al-rich samples, a 12![]() m resonance band
shows up in the small particle spectra in addition to the 13
m resonance band
shows up in the small particle spectra in addition to the 13![]() m
band feature. In other words, Al-rich spinels show spectra intermediate
between those of stoichiometric spinel and those of
m
band feature. In other words, Al-rich spinels show spectra intermediate
between those of stoichiometric spinel and those of ![]() -Al2O3.
This result is consistent with those of other authors
(Hafner & Laves 1961; Chihara et al. 2000).
-Al2O3.
This result is consistent with those of other authors
(Hafner & Laves 1961; Chihara et al. 2000).
By deriving mean residual emission profiles in the 12-18![]() m and
26-39
m and
26-39![]() m wavelength regions from ISO spectra of oxygen-rich AGB stars,
we have shown that near-stoichiometric spinel is indeed an excellent candidate
for the carrier of the emission features at 13, 16.8
m wavelength regions from ISO spectra of oxygen-rich AGB stars,
we have shown that near-stoichiometric spinel is indeed an excellent candidate
for the carrier of the emission features at 13, 16.8![]() m, and a newly dicovered one
at 32
m, and a newly dicovered one
at 32![]() m. Nonstoichiometry with Al/Mg ratios larger than 2.5 is not compatible
with the observed dust features.
m. Nonstoichiometry with Al/Mg ratios larger than 2.5 is not compatible
with the observed dust features.
The derivation of optical constants of refractory oxides is only a first step in studying the role of these substances in the context of circumstellar dust formation. A rather straightforward application of our results is to calculate equilibrium dust temperatures as functions of the distance from the stellar photosphere (see Woitke 1999, Fig. 2). A second, more sophisticated way to obtain additional information on the formation of oxides around M-giants will be condensation experiments. We have to leave these tasks up to future investigations.
Acknowledgements
We thank Gabriele Born, Jena, for preparing our samples. Anton Beran, Institut für Mineralogie und Kristallografie, Universität Wien, kindly provided us with various synthetic and natural minerals. Josef Hron gave us hints for the reduction of the spectra from his open time project. Thomas Henning's and an anonymous referee's suggestions helped to improve our original manuscript.
This work was supported by the Deutsche Forschungsgemeinschaft, DFG project number Do 575/4-1 and by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung under project number S7308-AST. TP received travels grant from the project FIRST-PACS/Phase I, financed by the Austrian federal ministry of transport, innovation and technology (bm:vit). FK's work was supported by APART (Austrian Programme for Advanced Research and Technology) from the Austrian Academy of Sciences.
The ISO Spectral Analysis Package (ISAP) is a joint development by the LWS and SWS Instrument Teams and Data Centers. Contributing institutes are CESR, IAS, IPAC, MPE, RAL and SRON.