N. Copernicus Astronomical Center, Department for Astrophysics, Rabianska 8, 87-100 Torun, Poland
Torun Center for Astronomy, N. Copernicus University, Gagarina 11, 87-100 Torun, Poland

Abstract
We have analysed the radio fluxes for 264 planetary nebulae for which reliable measurements of fluxes at 1.4 and 5 GHz, and of nebular diameters are available. For many of the investigated nebulae, the optical thickness is important, especially at 1.4 GHz. Simple models like the one specified only by a single optical thickness or spherical, constant density shells do not account satisfactorily for the observations. Also an r^-2 density distribution is ruled out. A reasonable representation of the observations can be obtained by a two-component model having regions of two different values of optical thickness. We show that the nebular diameters smaller than $10\hbox{$^{\prime\prime}$ }$ are uncertain, particularly if they come from photographic plates or Gaussian fitting to the radio profile. While determining the interstellar extinction from an optical to radio flux ratio, caution should be paid regarding optical thickness effects in the radio. We have developed a method for estimating the value of self absorption. At 1.4 GHz self absorption of the flux is usually important and can exceed a factor of 10. At 5 GHz self absorption is negligible for most of the objects, although in some cases it can reach a factor of 2. The Galactic bulge planetary nebulae when used to calibrate the Shklovsky method give a mean nebular mass of $0.14\, M_{\odot}$ . The statistical uncertainty of the Shklovsky distances is smaller than a factor of 1.5.

Key words: planetary nebulae: general - radio continuum: ISM - ISM: dust, extinction

Planetary nebulae emit in radio wavelengths due to free-free transitions in the ionized gas. Numerous analyses of individual objects and statistical studies of large samples often use the radio flux as one of principal observational parameters. The radio measurements, being free from interstellar extinction, provide us with direct information on nebular emission and can be used for determining luminosities and nebular masses. If a sufficiently high spatial resolution is available, the radio observations can be used for studying the structure of the nebulae and, in particular, to derive nebular dimensions. Radio surveys are also useful for identifying new planetary nebulae, especially in distant, heavily dust obscured regions, for instance in the Galactic bulge. Finally, comparison of the observed radio flux to the flux in optical recombination lines (usually H $\beta$ ) is one of the methods for measuring interstellar extinction to the planetary nebulae.

Unlike in the optical region, the planetary nebulae in the radio frequencies can be optically thick. This is expected to occur especially for young, dense nebulae observed at lower frequencies. If it happens optical thickness effects have to be taken into account while interpreting the radio measurements.

Systematic surveys of planetary nebulae have usually been done for single frequencies. Until recently the largest data sets have been available for 5 GHz. Surveys have been done with single dish telescopes (e.g at Parkes - Milne & Aller 1975; Milne 1979) and with multi dish instruments (mostly with VLA - e.g. Zijlstra et al. 1989; Aaquist & Kwok 1990). Recently a large set of flux measurements have been published for 1.4 GHz by Condon & Kaplan (1998). The data come from the NRAO VLA Sky Survey and the flux measurements have been done for 680 planetary nebulae.

In this paper we present results of an analysis of the observed fluxes at 1.4 and 5 GHz for a large sample of planetary nebulae. We have selected those objects for which reliable flux measurements at both frequencies are available and for which nebular dimensions are known. In this way we have obtained a sample of 264 planetary nebulae. With these data we can study optical thickness effects and test simple nebular models. An analysis of the consistency of the data allows us to draw conclusions on accuracy of the measurements. With additional observational data from the optical region, we discuss problems relevant to observational determination of interstellar extiction and distances.

2 Observational data

The observational data we have used in the present study are given in Table 1. Column (1) contains the PN G numbers while usual names of the planetary nebulae are given in Col. (2).

Column (3) gives the flux measurements at 1.4 GHz (in mJy) from Condon & Kaplan (1998). We have retained only those objects for which the accuracy of the measurements, according to Condon & Kaplan, is better than 10%.

The observed fluxes at 5GHz (in mJy) with the references are given in Cols. (4) and (5), respectively. We have restricted our compilation to the results from VLA only. Our preliminary analysis has shown that the measurements from single dishes (mostly from Parkes) do not give consistent results for optically thin nebulae (for more discussion see Sect. 3.1). From the VLA results we have dismissed objects with uncertain (according to remarks in the original papers) flux measurements. We have also excluded objects with the measured 5 GHz flux below 10 mJy (as less reliable according to Stasinska et al. 1992) unless two independent observations gave consistent results or the data come from carefull observations specially done to measure faint planetaries (e.g. Pottasch & Zijlstra 1994).

Columns (6)-(10) contain data on the observed nebular dimensions. The angular diameters (in arcsec) derived from radio observations (in overwhelming cases at 5 GHz) with the references are given in Cols. (6) and (7), respectively. For well resolved nebulae the diameters have been derived from the radio contours at 10% of the peak flux density. In other cases the data have usually come from Gaussian fitting. Some authors (e.g. Zijlstra et al. 1989; Aaquist & Kwok 1990) have deconvolved the results according to the model of Panagia & Walmsley (1978), which essentially resulted in multiplying the Gaussian angular diameter by factor 1.8. We have done the same if only Gaussian diameters have been published in original papers.

The nebular diameters (in arcsec) obtained from optical observations are shown in Col. (8). The relevent references are given in Col. (9). When possible we have chosen the data from H $\alpha$ (or H $\alpha$ + [NII]) images. In the case of objects having extended, diffuse outer structures or haloes we have taken the diameters corresponding to the bright main nebula. Unfortunately we have not been able to use many of the dimensions published in more recent CCD image catalogues (Schwarz et al. 1992; Manchado et al. 1996; Górny et al. 1999). They corresponded to the maximum extension of the recorded nebular emission and it was often clear from the published images that the principal nebular emission came from a much smaller, central region. In many cases the dimensions are from photographic plates and the results are expected to be more uncertain, especially for small nebulae. ST stands for "stellar".

The nebular diameter is a crucial parameter for our study presented in the subsequent sections. Yet it is often an ill defined or uncertain quantity either due to intrinsic (complex and irregular) structure of the object or due to the method used to measure the diameter. It would be ideal to have a quantity determined in the same way for all the objects, i.e. from the extension of the nebular emission at a 10% level of the peak value. It is clear that in our compilation the data are of different reliability. From a closer inspection of the observational material used to determine the dimensions, we have attempted to flag the more reliable measurements. They are marked with a + sign in Cols. (6) and (8). In the case of the radio diameters, these are objects for which the published maps were of good resolution and good dynamic range. These diameters have primarily been derived from the contours at 10% of the peak flux density. For optical measurements, this concerns well resolved nebulae, usually with a well defined outer rim.

In Col. (10) we give our adopted diameters. If the radio data were consistent with the optical measurements, we have simply taken a mean value from the two. In cases of discrepant data we have adopted values which tend to be closer to more reliable estimates, e.g. having assigned a + sign. For small nebulae ( ${<} 10 \hbox{$^{\prime\prime}$ }$ ) we have tended to adopt the radio measurements especially if the optical data came from photographic plates.

3 Analysis of the data and theoretical modelling

In the case of optically thin emission, standard theoretical formulae (see e.g. Pottasch 1984) predict the ratio of the flux at 5 GHz (actually 4.885 GHz) to that at 1.4 GHz to be 0.883. As can be seen from Table 1, for many objects the observed ratio is well above this value. A straightforward interpretation is that these planetary nebulae are not optically thin in the radio frequencies. The optical thickness is always larger for lower frequencies. Therefore the 1.4 GHz flux is expected to be more surpressed by self absorption and the 5 GHz to 1.4 GHz flux ratio should increase with the increasing optical thickness. In the optically thick case, when the emitted spectrum approaches the black body limit, the flux ratio reaches the value of 12.18.

In order to analyse the problem quatitatively we have plotted the 5 GHz to 1.4 GHz flux ratio against the radio brightness temperature, $T_{\rm b}$ , calculated from the 5 GHz flux and the adopted angular diameter. If the flux is expressed in mJy and the diameter, $\Theta$ , in arcsec then the brightness temperature in K can be determined from

The resulting diagram is shown in Fig. 1. The points represent the observed positions of the objects from Table 1. The curves give the theoretical predictions calculated from the basic model described in the following subsection.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f1.eps} % \end{figure}$

Figure 1: The 5GHz to 1.4GHz flux ratio against the radio brightness temperature at 5 GHz. Curves show predictions from the basic model for three values of $T_{\rm e}$ , i.e. $0.5\times 10^4$ K (dashed), $1.0\times 10^4$ K (full) and $1.5\times 10^4$ K (dotted).

3.1 Basic model

Suppose that the nebula is a uniform region characterized by an electron temperature, $T_{\rm e}$ , and an optical thickness, $\tau_0$ , at a reference frequency $\nu_0$ . For other frequencies the optical thickness is given as (see e.g. Pottasch 1984)

As can be seen from Fig. 1, for low values of $T_{\rm b}$ the observed points are scattered around the optically thin limit. For the nebulae with log $T_{\rm b} < 1.5$ (54 objects) the mean value of log $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ is -0.044 with a standard deviation of 0.104. The mean value agrees with the optically thin theoretical limit. The deviation can be considered as a typical accuracy of the observed flux ratio in our sample.

A diagram similar to that in Fig. 1 but using the 5 GHz fluxes from single dish measurements (mostly from Parkes - Milne & Aller 1975; Milne 1979; the 1.4 GHz flux from VLA - Table 1) shows the observed points for low $T_{\rm b}$ nebulae to be often well above the theoretical value. For 21 objects with log $T_{\rm b} < 1.5$ the mean log $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ is +0.045 with a deviation of 0.121. The reason can be twofold. First, the single dish measurements, as done with a lower angular resolution than those from VLA, can be contaminated from nearby faint sources. Second, the VLA flux may refer only to the main bright nebula as VLA can be insensitive to faint, extended outer nebular regions or halos. In any case the single dish measurements at 5 GHz give inconsistent results with the VLA data at 1.4 GHz and therefore we have limited our analysis to the 5 GHz fluxes from VLA only.

Returning now to the discussion of Fig. 1 we see that with the increasing $T_{\rm b}$ the observed flux ratio increases in a general agreement with the model curves. Thus the conclusion is that indeed many planetary nebulae in our sample are not optically thin, at least at 1.4 GHz.

As can be seen from the model curves in Fig. 1 the position in this diagram depends not only on the optical thickness but also on the electron temperature in the nebula. In fact a simplistic interpretation of Fig. 1 could be that many planetary nebulae have very low $T_{\rm e}$ , i.e. well below $0.5\times 10^4$ K, and that the most opaque nebulae tend to have high $T_{\rm e}$ . However, measurements of $T_{\rm e}$ from optical forbidden line ratios (e.g. Kaler 1986) usually do not give values as low as $0.5\times 10^4$ K. On the other hand, the most opaque nebulae are certainly the youngest ones and are presumably ionized by relatively cool central stars. Thus they are expected to have low $T_{\rm e}$ .

In order to avoid ambiguities due to $T_{\rm e}$ and to concentrate the discussion on the optical thickness problems, later on in this paper, we use the ratio $T_{\rm b}/T_{\rm e}$ instead of $T_{\rm b}$ . As can be seen from Eq. (4) this ratio depends on the optical thickness only.

Obviously for the observed objects we need estimates of their $T_{\rm e}$ . Unfortunately, direct measurements of $T_{\rm e}$ , e.g. from forbidden line ratios, are available for a limited number of objects only. However, as shown in Kaler (1986) the electron temperature measured from the [OIII] line ratio is well correlated with the line intensity of HeII $\lambda 4686$ Å. In this way, using a compilation of the HeII $\lambda 4686$ Å line intensity from Tylenda et al. (1994), we have been able to estimate $T_{\rm e}$ for the planetary nebulae in our sample. For 35 objects, however, there have been no measurements of the HeII $\lambda 4686$ Å line. In these cases we have adopted the canonical value of $T_{\rm e}$ for planetary nebulae, i.e. $1.0\times 10^4$ K.

A diagram of the 5 GHz to 1.4 GHz flux ratio plotted against $T_{\rm b}/T_{\rm e}$ is shown in Fig. 2. The full curve represents the results of our basic model as described above. Other curves show other models described below.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f2.eps}\end{figure}$

Figure 2: The 5GHz to 1.4GHz flux ratio against $T_{\rm b}/T_{\rm e}$ . Solid line: basic model, dotted line: spherically symmetric shell with $R_{\rm in} / R_{\rm out} = 0.95$ , dashed line: r^-2 density distribution.

As can be seen from Fig. 2 the observed positions tend to be shifted to the upper-left in comparison to our basic model (full curve). The effect is best seen for the objects with $$-2.5 \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaysty... ...ffinterlineskip\halign{\hfil$\scriptscriptstyle ...$ . The discussed model is very simple and can be considered as a very crude representation of real nebulae. Therefore we have attempted other models that are supposed to be more realistic.

3.2 Spherically symmetric shell

First we have analysed a spherically symmetric model in which the absorption coefficient is constant between an inner and an outer radius. The flux and the surface brightness temperature can be calculated from numerical integration of the radiation transfer equation. The results, i.e. the flux ratio and $T_{\rm b}/T_{\rm e}$ , for a particular model nebula depends on two parameters, namely the ratio of the inner to outer radius and the optical thickness of the nebula across its centre. It appears, however, that the results from this model are very much the same as those from the basic model, especially for largely filled envelopes. For thin shells the difference increases but always remains small compared to the scatter of the observational points. This is illustrated in Fig. 2 where a model having the inner to outer radius ratio equal to 0.95 is displayed (dotted curve).

3.3 $\mathsfsl{r^{-2}}$ density distribution

In theoretical modelling of radio emission from circumstellar envelopes it is sometimes adopted that the density of the emitting matter varies as r^-2 (or $r^{-\alpha}$ in its more general form), where r is the distance from the central star (e.g. Panagia & Felli 1975; Taylor et al. 1987). This sort of density distribution results from a simple steady-state wind model. We have also attempted to compare this kind of model to our observational data.

The nebular matter is assumed to be distributed spherically symmetrically. Starting from $R_{\rm in}$ the nebular density varies as $(r/R_{\rm in})^{-2}$ which implies that the absorption coefficient varies as $(r/R_{\rm in})^{-4}$ . As in the previous subsection the flux has been calculated from numerical integration of the radiation transfer equation.

The radio brightness temperature for a given model nebula has been derived in a way similar to that usually applied for observed objects. The surface brightness distribution across the nebular disc has been calculated. Then the nebular radius has been defined as a distance from the centre of the nebular disc to the place where the surface brightness drops to 10% of its maximum value. With this radius and the flux (both done for 5 GHz) the radio brightness temperature has been derived from Eq. (1).

The results are shown as a dashed curve in Fig. 2. As expected from analytical considerations (e.g. Panagia & Felli 1975) for large optical thicknesses ( $T_{\rm b}/T_{\rm e} \simeq 1$ ) $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ approches a limit of 2.12. This is much smaller than the limiting values in the previous models. The reason is that for optically thick r^-2distributions the radius of the emitting nebular disc increases with the decreasing frequency ( $\sim \nu ^{-0.7}$ - see e.g. Panagia & Felli 1975). Thus although the surface brightness of the nebular disc is close to that of the black body ( $\sim \nu ^2$ ) the flux is less steep ( $\sim \nu ^{0.6}$ ).

As can be seen from Fig. 2 the r^-2 model (dashed curve) does not fit the observed positions. It makes the discrepancy between theory and observations even larger when compared to the previous models. One may argue that it is more realistic to consider r^-2 density distributions with an outer cutoff due to the ionization front, as in Taylor et al. (1987). Then the results depend on the ratio of inner to outer radii, denoted by $\eta$ in Taylor et al. However, for $$\eta \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaysty... ...\offinterlineskip\halign{\hfil$\scriptscriptstyle ...$ the results are very close to the dotted (uniform shell model) and full (basic model) curves in Fig. 2. Only for $\eta < 0.3$ does the r^-2 density distribution deviate noticeably from the basic model, but towards the dashed curve (infinite r^-2).

Thus, contrary to Taylor et al. (1987), we conclude that the r^-2 density distribution is not typical for the planetary nebulae. This conclusion is consistent with what we can learn from observed images and hydrodynamical modelling of planetary nebulae. Images in optical emission lines (e.g. Balick 1987; Manchado et al. 1996; Górny et al. 1999) clearly show that they cannot be reconciled with the r^-2 density distribution in the great majority of the planetary nebulae. Hydrodynamical simulations of formation and evolution of planetary nebulae (e.g. Marten & Schönberner 1991; Corradi et al. 2000) predict the density structure significantly different from the r^-2 law, as well.

3.4 Two-component model

It is well known that most of the planetary nebulae do not show spherical symmetry. Often brighter and denser regions in the form of bipolar structures, blobs or condensations are embedded in fainter and thinner material. In order to investigate this situation we have constructed a two-component model which is a modification of our basic model in Sect. 3.1.

We adopt that the image of the nebula, while seen by an observer, consists of denser and more opaque regions characterized by an optical thickness, $\tau_\nu$ , and thinner regions having the optical thickness $\epsilon \tau_\nu$ . The thicker regions fill up a solid angle of $\xi \Omega$ , where $\Omega$ is the solid angle of the nebula as a whole. Correspondingly, the thinner regions fill up $(1 - \xi)\Omega$ . Both kinds of regions have the same electron temperature, $T_{\rm e}$ .

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f3.eps} % \end{figure}$

Figure 3: Comparison of the basic model (dotted curve) and the two-component model with $\xi =0.27$ and $\epsilon =0.19$ (full curve) with the observed nebulae having more reliable determinations of the diameters (+ signs in Table 1).

Therefore for a quantitative comparison between the observations and the two-component models we have selected a subsample of objects for which the diameters ("radio" and/or "optical") have been assigned with + in Table 1. We expect (as explained in Sect. 2) that these objects have relatively accurate values of the diameters. The resultant subsample (129 objects) is plotted in Fig. 3.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f4.eps} % \end{figure}$

Figure 4: The 90% confidence level of the $\chi ^2$ test of the two-component model. The cross shows the best fit.

As can easily be seen, the observed positions plotted in Fig. 3 are much better reproduced by the basic model (dotted curve) than those displayed in Fig. 2. However, the fit is not perfect. For intermediate values of log $T_{\rm b}/T_{\rm e}$ the observed positions still tend to be shifted to the upper-left from the dashed curve. A better fit to the observations can be obtained from a two-component model. The full curve shows a model with $\xi =0.27$ and $\epsilon =0.19$ which gives the best fit to the observations according to the $\chi ^2$ test. The $\chi ^2$ calculations have been done adopting that the typical error of the observed flux ratio is 0.075 in dex. This is the observed dispersion of the data for optically thin nebulae, i.e. having log $T_{\rm b}/T_{\rm e} < -2.5$ in Fig. 3 (39 objects, the mean value of the flux ratio is -0.049 in dex). The $\chi ^2$ minimum is, however, rather shallow. This can be seen from Fig. 4 which shows the 90% confidence level of the $\chi ^2$ test in the $\xi - \epsilon$ plane. Thus, roughly speaking, a reasonable fit of the model to the data in Fig. 3 is obtained for $$0.1 \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyl... ...\offinterlineskip\halign{\hfil$\scriptscriptstyle ...$ and $$0.15 \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaysty... ...offinterlineskip\halign{\hfil$\scriptscriptstyle ...$ .

It may seem, perhaps at first sight, that the two-component model (full curve) makes only a minor improvement of the fit in Fig. 3 as compared to the basic model (dotted curve). That this is not the case can be see from Fig. 4 which shows that the basic model ( $\xi = 1.0$ and/or $\epsilon = 1.0$ ) is significantly apart from the 90% confidence level of the two-component model. The $\chi ^2$ distance of the basic model from the best two-component model ( $\xi =0.27$ and $\epsilon =0.19$ ) is 39.2. This means that the ratio of the confidence level for the basic model to the confidence level for the best two-component model is much less than 0.01%. Thus the two-component model presents a significant improvement over the basic model.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f5.eps} % \end{figure}$

Figure 5: R versus the observed flux at 5 GHz. Full symbols: objects denoted with a + sign in Col. (6) of Table 1. Open symbols: other objects.

4 Uncertainities in the observational data

It is obvious that the observational data we are using in the present study are not free of uncertainties. As we have concluded from the data for optically thin nebulae in Sect. 3.1, a typical accuracy of the flux ratio in our sample is 0.10 (in dex). However, the accuracy need not be the same for the whole sample. For instance, it can be expected that the fluxes are more uncertain for faint objects, while the diameters are less precise for small nebulae. In this section we discuss possible sources of uncertainties in our observational data.

We consider the two-component model with $\xi =0.27$ and $\epsilon =0.19$ , shown by the full curve in Fig. 3, as a "reference" model for our sample. As found in Sect. 3.4 it reproduces satisfactorily the subsample of more accurately measured objects. Using the observed value of $T_{\rm b}/T_{\rm e}$ for a given object, we can predict the $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ ratio from the reference model. Then we define R as a ratio of the observed $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ to the predicted $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ . Thus the value of R is a measure of departure of the data for a given object from the reference model. In the following we analyse whether this departure correlates with the observed fluxes and diameters.

In Fig. 5 we have plotted R versus the observed flux at 5 GHz. Full symbols denote objects with more reliable measurements of the nebular diameter (+ signs in Cols. (6) or/and (8) of Table 1). In the whole range of log $F_{\rm 5GHz}$ the mean value of log R for the entire sample (264 objects) is within 0.03-0.05 while the standard deviation is 0.12. The full symbols (129 objects) show a somewhat lower deviation, i.e. 0.09.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f6.eps} % \end{figure}$

Figure 6: R versus the observed flux at 1.4 GHz. Full symbols: objects denoted with a + sign in Col. (6) of Table 1. Open symbols: other objects.

The same but for the observed flux at 1.4 GHz is given in Fig. 6. While the mean value of log R is here also within 0.03-0.05 the standard deviation is higher for fainter objects. For log $F_{\rm 1.4GHz} > 1.3$ in the whole sample (149 objects) the standard deviation is 0.09 while is it equal to 0.15 for log $F_{\rm 1.4GHz} < 1.3$ (115 objects). When only the full symbols are considered, the standard deviation is, respectively, 0.08 (88 objects) and 0.10 (41 objects).

The conclusion that can be drawn from Figs. 5 and 6 and the values of the standard deviation is that perhaps certain measurements of $$F_{\rm 1.4GHz} \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\... ...{\offinterlineskip\halign{\hfil$\scriptscriptstyle ...$ mJy might be less accurate. However, since the large deviation for log $F_{\rm 1.4GHz} < 1.3$ is primarily due to the open points uncertainities in the diameters can also be involved.

A plot of R against the adopted nebular diameter (Col. (10) in Table 1) indicates that the standard deviation for nebulae smaller than $10\hbox{$^{\prime\prime}$ }$ is higher, especially if the objects without a + sign in Table 1 are considered. Since our adopted diameters have been derived from a compilation of different observational data and different methods, in the following we will discuss separately the radio diameters and the optical diameters.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f7.eps} % \end{figure}$

Figure 7: R versus the radio nebular diameter. Full symbols: objects denoted with a + sign in Col. (6) of Table 1. Open symbols: other objects.

In Fig. 7 we have plotted the value of R against the radio diameter. Note that also the radio (and not adopted) diameter has been used to derive the value of R. Full symbols correspond to the data having a + sign in Col. (6) of Table 1. As mentioned in Sect. 2 these values primarily come from the 10% radio contours. Other objects, with measurements primarily resulting from a Gaussian deconvolution, are denoted with open cirles. As can be seen the full circles in Fig. 7 give a fairly consistent result. In the whole range of log $\Theta$ the mean value of log R is close to 0.02. For log $\Theta > 1.0$ (26 objects) the standard deviation is 0.06 comparing to the value of 0.09 obtained for log $\Theta < 1.0$ (95 objects). The other radio diameters (open symbols in Fig. 7) give more dispersed results. For log $\Theta > 1.0$ (9 objects) the mean log R is 0.03 with a standard deviation of 0.07. However, for log $\Theta < 1.0$ (122 objects) the corresponding values are 0.01 (mean) and 0.16 (standard deviation). Thus we can conclude that the radio diameters for small nebulae, especially if they are derived from the Gaussian fitting, are less certain. However, they do not show any significant systematic effect in the results.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f8.eps} % \end{figure}$

Figure 8: R versus the optical nebular diameter. Full symbols: objects denoted with a + sign in Col. (8) of Table 1. Open symbols: other objects. Objects with upper limits or denoted with ST. in Col. (8) of Table 1 are not included.

Figure 8 shows the same as Fig. 7 but using the optical diameters. Objects with upper limits or denoted with ST. in Col. (8) of Table 1 are excluded from the diagram. Similarily as in the previous figure the distribution of the full symbols in Fig. 8 is independent of the diameter although the statistics is here lower (30 objects only) and concerns relatively large nebulae. Nevertheless, for both, log $\Theta > 1.0$ and log $\Theta < 1.0$ , the mean value of log R is 0.02-0.03 and the standard deviation is 0.09-0.10. However the open symbols which primarily concern smaller nebulae show a larger spread and tend to be systematically above the line log R = 0.0. For log $\Theta > 1.0$ (23 objects) we have obtained the mean value of log R equal to 0.11 and the standard deviations of 0.21. For log $\Theta < 1.0$ (145 objects) the result is $0.08 \pm 0.14$ . The optical measurements for the objects denoted with the open symbols have mostly been derived from photographic plates. We conclude that they are often uncertain and tend to overestimate the diameters.

Summarizing the present section, it seems that the accuracy of the flux measurements is more or less uniform in our sample. Perhaps only for some objects the flux at 1.4 GHz measured to be below 20 mJy is more uncertain. The accuracy of the diameter measurements is however significantly worse for nebulae smaller than $10\hbox{$^{\prime\prime}$ }$ . This particularly concerns determinations from low angular resolution observations, i.e. results from photographic plates and Gaussian fitting to radio profiles.

5 Self absorption effects and derivation of interstellar extinction

The value of interstellar extinction of the planetary nebulae is often derived from an optical to radio flux ratio. This is usually done assuming that the nebulae are optically thin. It is quite obvious that this is not the case at 1.4 GHz for many objects in our sample. The fact that $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ is often measured to be well above the optically thin limit is primarilly due to self absorption at 1.4 GHz. At 5 GHz self absorption is always less important but it does not mean that it is always negligible.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f9.eps} % \end{figure}$

Figure 9: The self absorption correction factor f against $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ . Thin curves: f at 1.4 GHz, thick curves: f at 5 GHz. Dashed curves: basic model, full curves: reference model (two-component model with $\xi =0.27$ and $\epsilon =0.19$ ).

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f10.eps} % \end{figure}$

Figure 10: The self absorption correction factor f against $T_{\rm b}/T_{\rm e}$ . Thin curves: f at 1.4 GHz, thick curves: f at 5 GHz. Dashed curves: basic model, full curves: reference model (two-component model with $\xi =0.27$ and $\epsilon =0.19$ ).

Let us define f as a ratio of the flux obtained adopting negligible optical thickness (i.e. from simple integration of the emission coefficient over the nebula) to that derived with self absorption taken into account. If f can be estimated than the observed radio flux has to be multiplied by this factor before deriving interstellar extinction. In principle the value of f can be derived either from $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ or from $T_{\rm b}/T_{\rm e}$ as both parameters measure optical thickness effects.

In Fig. 9 we have plotted f at 1.4 GHz (thin curves) and 5 GHz (thick curves) against $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ calculated from the basic model (dotted curves) and the reference model (full curves). The same but displayed against $T_{\rm b}/T_{\rm e}$ is shown in Fig. 10. (Note that $T_{\rm b}$ in Fig. 10, as throughout in this paper, refers to 5 GHz.)

As can be seen from Figs. 9 and 10 the relations between f and the observational quantities are model dependent. Generally speaking, for a given value of the flux ratio or $T_{\rm b}/T_{\rm e}$ the two-component model predicts a larger f than the basic model. For the two-component model the relations in Figs. 9 and 10 depends on the model parameters, i.e. $\xi$ and $\epsilon$ .

We have estimated f for the objects in our sample. We have adopted the reference model ( $\xi =0.27$ and $\epsilon =0.19$ ). f has been estimated from the observed $F_{\rm 5GHz}/F_{\rm 1.4GHz}$ and $T_{\rm b}/T_{\rm e}$ , and the mean value from the two has been taken. Figure 11 plots the flux at 5 GHz corrected for self absorption, i.e. observed multiplied by f, against the observed flux. The same but for 1.4 GHz is shown in Fig. 12.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f11.eps} % \end{figure}$

Figure 11: The flux at 5 GHz corrected for self absorption against the observed flux. Full line: the 1:1 relation.

As can be seen from Fig. 11, for most of the objects the self absorption at 5 GHz is not important. In a few cases, however, it can be as large as factor 2. As expected, the self absorption at 1.4 GHz is much more important. As can be seen from Fig. 12, in a number of cases it is of the order of 10.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f12.eps} % \end{figure}$

Figure 12: The flux at 1.4 GHz corrected for self absorption against the observed flux. Full line: the 1:1 relation.

Estimates of the self absorption factor are usually done in the literature from the observed $T_{\rm b}$ and formulae which are equivalent to our basic model (e.g. Condon & Kaplan 1998). As can be seen from Fig. 10 this leads to smaller correction factors than those from our procedure based on the reference model. We have repeated our estimates as described above but using the basic model. The resultant correction factors, $f_{\rm basic}$ , are indeed smaller than the previously derived f values. The relation between the two estimates can be very well approximated by $\log\, f_{\rm basic} = \alpha \,\log\, f$ . For the flux at 5 GHz $\alpha \simeq 0.61$ whereas at 1.4 GHz $\alpha \simeq 0.87$ . Thus at 1.4 GHz where f can be as large as 10 the basic model predicts the correction factor about 30% lower than the reference model.

As explained above our procedure for deriving f relies on the flux ratio and the brightness temperature at 5 GHz. In principle, one can also use the brightness temperature at 1.4 GHz, as done, for instance, in Condon & Kaplan (1998) while correcting the fluxes at 1.4 GHz. The advantage of our approach is that it allows to estimate the self absorption even for quite opaque nebulae at 1.4 GHz. As can be seen from Figs. 9 and 10, from both, the flux ratio and $T_{\rm b}$ at 5 GHz, the correction factor at 1.4 GHz (thin curves) can be reliably estimated up to values of 20-30. The relation between f at 1.4 GHz and $T_{\rm b}$ at 1.4 GHz is described by the thick curves in Fig. 10 (the same as for both quantities at 5 GHz). Clearly it becomes useless for the self absorption greater than 2-3.

Stasinska et al. (1992) have found that there is a systematic difference between the extinction derived from the Balmer decrement, $C_{\rm opt}$ , and from the ratio of 5 GHz to H $\beta$ fluxes, $C_{\rm rad}$ . We have repeated their analysis for objects in our sample adopting our correcting precedure for self absorption at 5 GHz. The logarithmic extinction at H $\beta$ , $C_{\rm rad}$ , has been calculated in a standard way (e.g. Pottasch 1984) using the observed H $\beta$ fluxes from Acker et al. (1992). The HeII $\lambda 4686$ Å line intensities from Tylenda et al. (1994) have been used in order to estimate the electron temperature and the ionization degree of helium. The observed values of H $\alpha$ /H $\beta$ have been taken from Tylenda et al. (1994). We have excluded objects for which the accuracy of the H $\beta$ flux (Acker et al. 1992) is worse than 0.1 in dex.

$\begin{figure} \par\includegraphics[width=7cm,clip]{10021f13.eps} % \end{figure}$

Figure 13: $C_{\rm opt}$ derived from the Balmer decrement versus $C_{\rm rad}$ from the 5 GHz to H $\beta$ flux ratio. Solid line: the 1:1 relation, dashed line: the orthogonal regression line.

The results are displayed in Fig. 13 which can be compared to Fig. 5 in Stasinska et al. The orthogonal regression line for the points in Fig. 13 is

6 Shklovsky distances to the planetary nebulae in the Galactic bulge

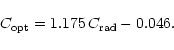
One of the most widely used (and most often criticized) methods for determining distances to the planetary nebulae is the Shklovsky method. The basic assumption in this method is that the nebulae have the same mass, usually adopted to be $0.2\, M_{\odot}$ . This is probably the most important source of uncertainties in the derived distances as the nebulae are expected to have an important spread in their masses.

A test (or a calibration) of a method for determining distances can be done if it can be applied to a sample of objects with known distances. This is the case of the planetary nebulae in the Galactic bulge. This sort of test of the Shklovsky method has been done in Stasinska et al. (1991) and in Pottasch & Zijlstra (1992). The two groups have drawn rather opposite conclusions. The Shklovsky distances derived in Stasinska et al. are compatible (for most of the objects within factor 2) with the known distance to the Galactic centre. Pottasch & Zijlstra conclude that the Shklovsky method is wrong as it systematically overestimates the distances.

We have calculated the Shklovsky distances for a sample of the Galactic bulge objects selected from Table 1. The selection has been done in a standard way, i.e. nebulae within $10\hbox{$^\circ$ }$ of the Galactic centre having a diameter smaller than $20\hbox{$^{\prime\prime}$ }$ and flux at 5GHz lower than 100 mJy. This resulted in a sample of 80 objects which is smaller than in the two previous studies. The reason is that our Table 1 includes only objects with reliable flux measurements at 5 and 1.4 GHz.

We have used the same formula as in Stasinska et al. (1991). The nebulae are assumed to have a mass of $0.2\, M_{\odot}$ and a filling factor of 0.5. The observed H $\beta$ fluxes (Acker et al. 1992) have been corrected for the interstellar extinction, $C_{\rm rad}$ , using the 5 GHz fluxes. Note that the radio fluxes have been corrected for self absorption and that the effects of the electron temperature and the He ionization degree have been taken into account, as explained in Sect. 5. We have used the "adopted" diameters from Col. (10) of Table 1. Note that the result would be practically the same if we took the "radio" values from Table 1 (Col. 6). This is not surprising since, as noted in Sect. 2, for small nebulae we have preferentially adopted the values from radio measurements.

Figure 14 shows a histogram of the obtained Shklovsky distances, $d_{\rm Shkl}$ . The mean value of log $\,d_{\rm Shkl}$ is 0.997 and the standard deviation is 0.167. The derived mean value (9.9 kpc) is somewhat larger than the current estimates of the distance to the Galactic centre which varies from 7 to 9 kpc depending on the method used (Reid 1999). However, we do not conclude that the Shklovsky method is wrong. Figure 14 can be used for calibrating the method and for estimating its accuracy.

The mean value of the Shklovsky distances would be equal to 8.5 kpc (the IAU-approved value for the distance to the Galactic centre) if the nebular mass adopted in the Shklovsky formula were $0.14\, M_{\odot}$ . In other words, if the Galactic bulge planetary nebulae are used to calibrate the Shklovsky method than the nebular mass of $0.14\, M_{\odot}$ should be adopted in the distance formula. An open question is, however, to what extend the planetary nebulae in the Galactic bulge can be regarded as representative for the whole Galactic population.

The standard deviation of the log $\,d_{\rm Shkl}$ distribution can be considered as an average error of the Shklovsky method. The distribution in Fig. 14 would thus imply that the Shklovsky distances are typically uncertain by a factor of 1.5. In the worst individual cases the error can reach a factor of 3. The internal uncertainty of the Shklovsky method (resulting primarily from the assumption of a constant nebular mass) is however smaller. In the case of the Galactic bulge nebulae the observational errors can be important, especially in the diameters to which the Shklovsky distances are most sensitive. The observed standard deviation in the Shklovsky distances could be entirely accounted for by a standard deviation in the diamaters equal to 0.3 in dex. A typical uncertainty of factor 2 in the diameters is probably too pessymistic. Nevertheless, the uncertainty is expected to be important as the Galactic bulge nebulae are mostly smaller than $10\hbox{$^{\prime\prime}$ }$ and their diameters primarily come from the radio Gaussian fitting (cf. discussion of Fig. 7 in Sect. 4).

7 Summary and conclusions

We have analysed the radio fluxes for 264 planetary nebulae. These are objects for which reliable measurements of fluxes at 1.4 and 5 GHz from VLA are available. Also nebular dimensions are known for them.

We have shown that for many of the investigated nebulae the optical thickness is important, especially at 1.4 GHz. We have attempted different nebular models in order to account for the observations. A simple model specified only by a single optical thickness is not satisfactory. The same has been concluded for spherically symmetric, constant density shells. A spherically symmetric models with an r^-2 density distribution has also been ruled out. A reasonable representation of the observations has been obtained from a two-component model in which the nebular image consists of regions having two different values of optical thickness.

We have analysed uncertainties in the observational data. The accuracy of the flux measurements is more or less uniform in our sample. Perhaps for some objects the flux at 1.4 GHz, if it is below 20 mJy, can be more uncertain. We have found that the uncertainity in the nebular diameters siginificantly increases for nebulae smaller that $10\hbox{$^{\prime\prime}$ }$ . This concerns the measurements from photographic plates and from Gaussian fitting to the radio profile.

While determining the interstellar extinction from an optical to radio flux ratio, caution should be applied to optical thickness effects in the radio. We have developed a method for estimating the value of self absorption. It relies on the observed radio flux ratio (5 GHz to 1.4 GHz) and the observed brightness temperature at 5 GHz. The results, however, depend on the adopted nebula model. At 1.4 GHz, self absorption of the flux is usually important and can exceed a factor of 10. At 5 GHz self absorption is negligible for most of the objects although in some cases it can reach a factor of 2. Similarily as in Stasinska et al. (1992) we have obtained a systematic difference between the extinction derived from the Balmer decrement and that from the optical to radio flux ratio. Our relation is however slightly less steep due to (usually small) corrections for self absorption of the 5 GHz fluxes in our study.

We have attempted to calibrate the Shklovsky method using the planetary nebulae in the Galactic bulge. The mean value of the Shklovsky distances is close to the distance to the Galactic centre if the nebular mass is adopted to be $0.14\, M_{\odot}$ . This is smaller than a canonic value of $0.2\, M_{\odot}$ usually adopted in the Shklovsky method. Unfortunately the question whether the Galactic bulge nebulae are typical for the whole Galactic population is still open. From the distribution of the Shklovsky distances for the Galactic bulge nebulae we have derived that the statistical uncertainity of the Shklovsky distances should be smaller than factor 1.5.

A study like that done in this paper could be much more accurate and conclusive if an extensive survey of the planetary nebulae, similar to those existing at 5 and 1.4 GHz, were available at a higher frequency. The fluxes at three frequencies would allow us to better test different model nebulae and to study more deeply the optical thickness effects. The flux at the higher frequency could be used with great confidence even for small and compact nebulae to derive interstellar extinction. In fact there is a survey at 14.7 GHz by Milne & Aller (1982) but this has been done with the Parkes telescope. In view of our experiences (this paper as well as Stasinska et al. 1992) high frequency measurements with the VLA would be desirable. However, the synthesized beam of the VLA, even in the most compact configuration, is very small at high frequencies. Thus, as discussed in Pottasch & Zijlstra (1994), the fluxes of extended planetary nebulae from this instrument could be systematically underestimated. Perhaps a survey with a large single dish, e.g. the 100 m Green Bank Telescope, would be more appropriate.

References

Online Material

References:
F(5 GHz) & radio diameter ref.:
1 - Zijlstra et al. (1989); 2 - Pottasch & Zijlstra (1994); 3 - Aaquist & Kwok (1990); 4 - Isaacman (1984); 5 - Ratag & Pottasch (1991); 6 - Gathier et al. (1983); 7 - Phillips & Mampaso (1988); 8 - Kwok et al. (1981); 9 - Basart & Daub (1987); 10 - Seaquist & Davis (1983); 11 - Rodriguez et al. (1985); 12 - Pottasch et al. (1988); 13 - Ratag et al. (1990); 14 - Zijlstra & Pottasch (1989).
Optical diameter ref.:
a - Perek & Kohoutek (1967); b - Kinman et al. (1988); c - Holmberg et al. (1977); d - Cahn & Kaler (1971); e - Dopita et al. (1990); f - Chu et al. (1987); g - Moreno et al. (1988); h - Schohn (1990); i - Acker et al. (1991); j - Weinberger (1977); k - Shaw (1985); l - Kohoutek & Martin (1981); m - Cahn & Kaler (1988); n - Kohoutek (1972); o - Shaw & Kaler (1985); p - Kohoutek (1969); r - Lauberts (1982); s - Manchado et al. (1989); t - Isaacman et al. (1980); u - Bedding & Zijlstra (1994); w - Manchado et al. (1996); z - Balick (1987).

Contents

An analysis of the observed radio emission from planetary nebulae

1 Introduction