4 The cluster luminosity function and the initial mass function

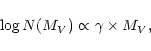
The luminosity function, LF, is a powerful tool to compare the distribution of massive stars in relation to less massive ones. Special care must be taken as the different evolutionary status of the stars present in a given sample can lead to wrong results. This is not the case in an open cluster. The LF shows the additional advantage that it is independent of the evolutionary model or theory used (Burki 1977). In order to build this function, it is assumed that such function may be considered a power law expressed as follows:

$$\log N(M_V)\propto \gamma \times M_V,$$

where $\gamma$, the slope of the fitting, is a quantity to be determined from our data. We list in Table 5 the star counts by M_V magnitude bins of size $\Delta M_V= 1$ mag. The most evolved members, the two WR stars, were included in the brightest bin while the faintest one was ignored because of its obvious incompleteness. The counts were fitted by means of an unweighted least squares method throughout two luminosity ranges, -8 < M_V < -1 or -8 < M_V < -3 to estimate the influence of incompleteness among faint stars. The $\gamma$ values obtained from the respective fittings are quite flat, $\approx$0.12, in relation to other regions in our galaxy and the Magellanic Clouds: Vallenari et al. (1993) found $\gamma =0.3$ in the range -2.5 < M_V < + 1 in the young association NGC 1948 in the LMC; Perry & Hill (1992) found $\gamma =0.3$ in the range -7 < M_V < - 4 in the association Scorpius OB1 and NGC 6231; Baume et al. (1999) found $\gamma \approx 0.2$ in NGC 6231 in the range -7.5 < M_V < 1.5. The slope of the luminosity function in HM1 is, indeed, flat because, apart from multiplicity and binarity effects or incompleteness due to the strong absorption, even if we raise the lower limit up to -4, the slope $\gamma$ remains unchangeable. The initial mass function, IMF, on the other hand, gives the number dN of stars of mass ${\cal M}$ in the mass bin ${\cal M}\pm {\rm d} {\cal M }/2$, found in an open cluster at the moment of its formation. This function can be well represented by a power law (see, e.g., Scalo 1986):

$${\rm d}N \propto {\cal M}^{-x} \times {\rm d}(\log {\cal M}).$$

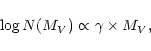
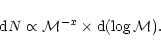
When dealing with galactic field stars, the slope of the IMF, x, has a typical value of 1.35 as found by Salpeter (1955). However, when dealing with open clusters, strong variations of x have been reported by Conti (1992) and Massey et al. (1995). In our case, to compute the x value in HM1 we used the mass-luminosity relation given by Scalo (1986) to transform the LF into the IMF. It assigns a mean mass to each luminosity bin. The stellar mass values and the corresponding counts, dN, listed in Table 5, were fitted with a least squares method. The result of the fittings yields extremely flat IMF slopes of x = 0.6-0.7. Anyway, if fitting errors are allowed, the slope value can still fit into the range 1.0 < x < 1.3 of typical slopes found in our galaxy according to Conti (1992). In terms of similarity with other objects of this type, the IMF of HM1 massive stars is indeed steep but not unusual: Massey et al. (1995) found IMF slopes ranging from 0.7 to 2 for 11 open clusters of our galaxy in the dominion of massive stars. Other flat slopes in open clusters are also reported in, for example, the works of Sagar et al. (1986) or Will et al. (1995).