| W | = | 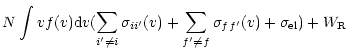 |
|
| d | = | 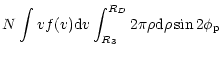 |
(1) |
The semiclassical perturbation formalism, as well as the corresponding computer code (Sahal-Bréchot 1969a,b), have been updated and optimized several times (Sahal-Bréchot 1974; Fleurier et al. 1977; Dimitrijevic & Sahal-Bréchot 1984; Dimitrijevic et al. 1991; Dimitrijevic & Sahal-Bréchot 1996b). The calculation procedure, with the discussion of updatings and validity criteria, has been briefly reviewed e.g. in Dimitrijevic & Sahal-Bréchot (1996a,b) so that only the basic details of calculations will be presented here. Stark full width (W) at the intensity half maximum (FWHM) and shift (d) of an isolated spectral line may be expressed as (Sahal-Bréchot 1996a,b; Fleurier et al. 1977):
| W | = | 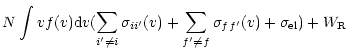 |
|
| d | = | 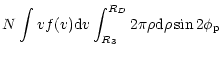 |
(1) |
where N is the electron density, f(v) the Maxwellian
velocity distribution function for electrons, ![]() denotes the
impact
parameter of the incoming electron, i and f denote the initial and
final
atomic energy levels, and i', f' their corresponding perturber levels,
while
denotes the
impact
parameter of the incoming electron, i and f denote the initial and
final
atomic energy levels, and i', f' their corresponding perturber levels,
while ![]() gives the contribution of the Feshbach resonances
(Fleurier et al. 1977). The inelastic cross section
gives the contribution of the Feshbach resonances
(Fleurier et al. 1977). The inelastic cross section
![]() can be
expressed by an integral over the impact parameter of the transition
probability
can be
expressed by an integral over the impact parameter of the transition
probability
![]() as
as
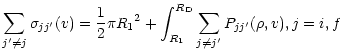 |
(2) |
and the elastic cross section is given by
| = | 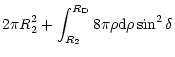 |
||
| = | (3) |
The phase shifts
![]() and
and
![]() due respectively to
the
polarization potential (r-4) and to the quadrupolar potential
(r-3), are given in Sect. 3 of Chap. 2 in Sahal-Bréchot (1969a).
due respectively to
the
polarization potential (r-4) and to the quadrupolar potential
(r-3), are given in Sect. 3 of Chap. 2 in Sahal-Bréchot (1969a).
![]() is the Debye radius. All the cut-offs R1, R2, R3 are described
in Sect. 1 of Chap. 3 in Sahal-Bréchot (1969b).
For electrons, hyperbolic
paths due to the attractive Coulomb force were used, while for
perturbing ions the paths are different since the force is repulsive.
The formulae for the ion-impact widths and shifts are analogous to
Eqs. (1-3), without the resonance contribution to the width. The difference
in calculation of the corresponding transition probabilities and phase
shifts as functions of the impact parameter in Eqs. (2) and (3) is in the
ion perturber trajectories which are influenced by the repulsive
Coulomb
force, instead of an attractive one as for electrons.
Atomic energy levels have been taken from Moore (1985).
is the Debye radius. All the cut-offs R1, R2, R3 are described
in Sect. 1 of Chap. 3 in Sahal-Bréchot (1969b).
For electrons, hyperbolic
paths due to the attractive Coulomb force were used, while for
perturbing ions the paths are different since the force is repulsive.
The formulae for the ion-impact widths and shifts are analogous to
Eqs. (1-3), without the resonance contribution to the width. The difference
in calculation of the corresponding transition probabilities and phase
shifts as functions of the impact parameter in Eqs. (2) and (3) is in the
ion perturber trajectories which are influenced by the repulsive
Coulomb
force, instead of an attractive one as for electrons.
Atomic energy levels have been taken from Moore (1985).
The contribution of ion impact widths and shifts to the total line widths
and shifts can be neglected
since our results for ![]() K are
two order of magnitude smaller.
K are
two order of magnitude smaller.
Copyright ESO 2001