2 High rejection nulling interferometry: Theoretical requirements

Let us consider a two wavefront pupil interferometer, set in flat field (the interference state is uniform over the whole area of interference). Theoretically, two wavefronts give perfect constructive (respectively destructive) interference if, on each point of the beam-combiner, they have the same amplitude, phase (respectively same phase but one wavefront is 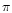$\pi$-shifted) and polarization state. This requires a perfect matching of the two wavefronts. Every differential distortion in amplitude, in phase or in the polarization state leads to a local modification of the interference state. If the interferometer is set in a dark flat field, it leads to a light leak through the interference pattern. In this paper, we will consider only the amplitude and phase distortions of the wavefronts because we are working in a monochromatic case with a linearly polarized laser.

One can easily show that a 10⁶ rejection rate could only be reached with a two wavefront interferometer if (Ollivier 1999):

i)

the mean phase difference, including optical path difference (OPD), does not exceed 2 10^-3 radian;

ii)

the mean differential intensity difference does not exceed 0.4% ( $\Delta I/I < 4~10^{-3}$).

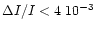These conditions, in terms of optical constraints, lead to the following optical requirements, estimated by numerical simulation (Ollivier & Mariotti 1997):

• less than 0.0002% of the optical surface covered by dust (0 transmission points);
  
• less than 0.5% inhomogeneity in the coating reflection coefficient;
  
• Phase control better than 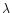$\lambda$/3000, from OPD to surface roughness scales (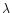$\lambda$ is the working wavelength);
  
• Pointing control of each telescope within 1/100th of the full width of the Airy disk.
  

Even if they are individually achievable, satisfying all of these requirements simultaneously would lead to a costly system.

Numerical simulations and calculations have already shown that these requirements could strongly be reduced if an optical filtering of the Airy figure of each telescope of the interferometer is performed, because:

i)

each telescope individually does not resolve the system star-planet, so all the information is contained inside the Airy disk;

ii)

a major part of phase and amplitude defects are high spatial frequency defects with effects outside the Airy disk. Thus, they are eliminated well by optical filtering.

Optical filtering can be performed by a pinhole (Ollivier & Mariotti 1997) or by single-mode waveguides (Mennesson et al. 2001). In the first case, a simple spatial filtering has to be considered: the higher the spatial frequency of the defect, the better the filtering efficiency. In the second case the filtering effect is obtained by the fact that only one mode propagates through a single-mode waveguide. The other modes of the corrupted wavefront (including tilt, higher order aberrations and substrate roughness) are eliminated through the propagation. The amplitude of the wavefront at the waveguide output depends on the coupling efficiency of the corrupted wavefront to the propagating mode, while the phase is a function of the mean phase before injection into the waveguide.

The first case will later be called "spatial filtering'' and the second "modal filtering''.