HD 152248: Evidence for interaction

5 Equivalent widths and S-S effect

Using a two-Gaussian fit, we measured the EWs of the primary and secondary absorption lines listed in Table 2, except near conjunction. Particular attention has been paid to the normalization process to avoid systematic deviations. We estimate that our continuum determination is self-consistent with an accuracy better than 0.5%. For the strongest lines, this corresponds to a maximum contribution to the error on the EW measurements of about 0.05 Å. We further estimate that the mean contribution of the continuum determination to the error is about 0.02 Å and that the intrinsic error related to the measurement process is of the same order of magnitude.

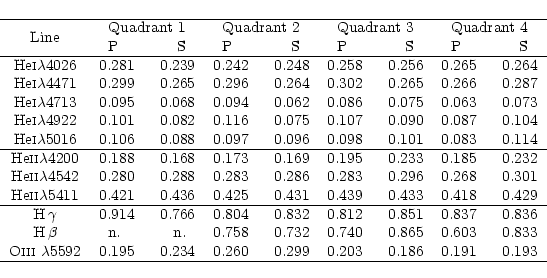
Several clear tendencies appear from these measurements and are presented below. First of all, let us divide the orbital cycle into four parts which we call quadrants, each of them corresponding to an interval of 90$^\circ$ in true anomaly. The first quadrant ranges then from the primary eclipse to the first quadrature; the second, from the first quadrature to the secondary eclipse and so on for the third and fourth quadrants. Due to the blend near conjunction, the effective corresponding phase intervals are, respectively for 1st to 4th interval, [0.06-0.22], [0.22-0.40], [0.66-0.80] and [0.80-0.95]. To limit the uncertainties and outline the observed trends, we computed the mean EWs over each of the quadrants. These are listed in Table 5. The primary to secondary ratios of the mean EWs in each quadrant are further plotted in Figs. 3 and 4.

  

Table 5: List of the mean equivalent widths (expressed in Å) over each of the four quadrants (see text). The P and S stand for Primary and Secondary respectively

$$\begin{tabular}{c l r l r l r l r} \hline Line & \multicolumn... ... 0.299 & 0.203 & 0.186 & 0.191 & 0.193 \\ \hline \end{tabular}$$

From these figures, we can identify the following trends:

1.

The He I lines: a very intriguing variation is observed for the He I$\lambda$4471 line and is also present in other He I lines. The primary to secondary EW ratio is reversed in the fourth quadrant. Indeed, during the first three quadrants, the lines associated with the primary are slightly more intense than the secondary ones. In the fourth quadrant (i.e. $\phi$ = 0.8-1.0) however the situation is exactly the opposite, with the primary's lines being fainter. Thus the secondary lines seem stronger between phases 0.8 and 1.0, when the star is approaching. However, we have to mention that this effect is not detected for the He I$\lambda$4026 line, but this line is actually a blend with the He II$\lambda$4026 transition;

2.

The He II lines: a clear enhancement of the secondary lines compared to the primary ones is observed for the He II$\lambda$$\lambda$4200 and 4542 lines during the 3rd and 4th quadrants, while the secondary is approaching. However the He II$\lambda$5411 line does not seem to display any significant variation of the EW ratio (Fig. 4);

3.

The Balmer lines: these lines do not seem to display such a clear general trend as the He I or He II lines. Indeed, although the four Balmer absorptions (i.e. H$\beta$, H$\gamma$, H$\delta$ and H$\epsilon$) most often exhibit the blueshifted component with the largest EW, this probably results, for the H$\delta$ and H$\epsilon$ lines, from a blend with neighbouring lines on the blue side. The H$\gamma$ line displays an inversion of the primary and secondary EW ratio between the 1st and 2nd quadrants. Finally, though none of the H$\beta$ spectra could be separated in the 1st quadrant, the secondary line is clearly strengthened when this star is approaching (i.e. quadrants 3 and 4). The primary line also seems fainter at those phases;

4.

The O III $\lambda$5592 line: this line displays a behaviour opposite to the ones of the lines previously discussed. In this case, the secondary line is fainter in the 3rd and 4th quadrants, while the secondary star is approaching.

As suggested by Howarth et al. (1997), these variations might be related to the so-called Struve-Sahade effect (S-S effect) though the origin of this effect is still not fully understood. First reported by Struve (1937), the Struve-Sahade effect is the apparent strengthening of the secondary spectrum of a hot binary when the secondary is approaching and the corresponding weakening of the lines when it is receding (Bagnuolo et al. 1999). We refer to the paper of Bagnuolo et al. for a recent review of the problem. In their paper, Bagnuolo et al. re-analysed three systems previously reported to display this effect and concluded that these ``three classical massive binaries [...] have a different tale'': localized heating by colliding winds for AO Cas, no Struve-Sahade effect for Plaskett's Star and a probable RLOF scenario for 29CMa. So the Struve-Sahade effect is thus probably a similar manifestation of different physical phenomena and must then be investigated one case at a time.

Strictly speaking, only H$\beta$ and two of the three studied He II lines display the S-S effect. Indeed, the variation of the He I line intensity does not match the ``classical'' definition of the S-S effect, as the strengthening of the secondary lines and the corresponding weakening of the primary ones occur between the 3rd and the 4th quadrants. A detailed investigation of the intrinsic variations of the EWs related to each star would further require correcting them for the relative contribution of the primary and secondary fluxes to the continuum. However, we have to defer this task to future works as we do not have at our disposal, at this stage, the appropriate photometric information required to properly carry out this study.

Finally, Gayley (2001) has recently suggested that the S-S effect might be due to surface flows generated by the irradiation of the stellar surface by the companion. This could modify the rotational broadening of the lines and might break down the approaching/receding symmetry, resulting in shallower or deeper absorption lines according to the line of sight. However, no influence on the intensity of the line is expected due to surface flows. The maximum projected velocity of such surface flows predicted in the case of the components of HD152248 lies near 110 kms^-1. The measured FWHMs of the absorption lines in the spectrum of HD152248 present a scatter of about 0.3-0.4 Å around the mean value, though no clear correlation with the phase is observed. This corresponds to a variation of the broadening velocity of about 25 kms^-1. The exact contribution of surface flows induced by irradiation to these slight profile variations is unknown. Clearly, detailed numerical modelling as well as more observations combining very high S/N and high resolution are needed to clarify this question.

Figure 5: Left: dynamical spectrum of the C III$\lambda$5696 emission line. The cuts are set to [0.97-1.08]. The He I$\lambda$4471 line RV curve has been overplotted. Right: RVs of the C III$\lambda$5696 line overplotted on the He I$\lambda$4471 line RV curve. The symbols used have the same signification as in Fig. 1

HD 152248: Evidence for interaction