A&A 369, 65-73 (2001)
DOI: 10.1051/0004-6361:20010100

New determination of the solar apex

Ch. Fehrenbach1,2 - M. Duflot1 - R. Burnage2


1 - Observatoire de Marseille, 2 place Le Verrier, 13248 Marseille Cedex 04, France
2 - Observatoire de Haute Provence, 04870 Saint Michel l'Observatoire, France

Received 4 August 2000 / Accepted 16 November 2000

Abstract
Many studies recently have been performed to determine the velocity vector of the Sun, mainly using the latest data on proper motions and parallaxes given by the Hipparcos satellite. We wished to carry out a similar study using totally independent data: the numerous radial velocities (RV) obtained with the Fehrenbach Objective Prisms (PO). This method allows the determination of the RVs of all the stars contained in the same field. These RVs are relative to each other but are linked to the IAU standard system by means of at least two calibration stars of known RV belonging to that field. These data are very homogeneous. We discuss the precision of the results, and deduce that this material is relevant for the computation of the movement of the Sun towards its Apex. We have performed several studies: 1) With 6965 stars of magnitudes ranging from 7 to 10, measured with the small PO of 15 cm diameter (PPO), with the whole sample and with the same sample split into blue and red stars. 2) With 11 978 stars of magnitudes ranging from 7 to 11, by adding to the previous sample the stars measured with the 60 cm diameter PO associated with the Schmidt telescope of Observatoire de Haute Provence (SPO). The results of both studies are consistent. 3) We have estimated the distance D of all stars studied and determined U, V, W and S for four groups of stars selected according to their distances: D<100,   100<D<300,    300<D<500,    D>500 parsecs. We have determined the variation of U, V, W and S with respect to the distance of the stars. The variation of U, V and S is linear up to 500 parsecs. We can consider that W is constant.

Key words: Galaxy: structure - stars: kinematics - techniques: radial velocity


1 Introduction

We have undertaken a series of systematic RV measurements to complete existing RV catalogues and also to search for high-RV stars. Their number has been found to be relatively small. Nevertheless, the set of data obtained appeared to be suitable to determine the motion of our sun with respect to the nearby stars. A certain number of such determinations have already been performed by other authors; the results depend essentially on the homogeneity of the sample used, as well as the number of its elements. Using the entire set of our data; we used the classical method (Mihalas & Binney 1981) to determine the solar Apex.

2 The measure of radial velocities ( $\mathsf{RV}$) with objective prisms (PO): Their accuracy

The RVs in this study were obtained by means of two normal-field POs (Fehrenbach 1944; Fehrenbach 1951). We give a short description of these instruments: the single prism of the ordinary PO is replaced by a composite prism constituted of a flint glass prism of angle 2A between two crown-baryum glass prisms of angle A mounted such as to form a parallel face plate (Fig. 1).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{cf10160fig01.eps} \end{figure} Figure 1: Principle of the normal field Objective Prism

The two glasses have the same refraction index for a given wavelength $\lambda_{\rm o}$ at approximately 422 nm; this wavelength is in the middle of the sensitivity domain of the blue photographic plates. (The glassmaker made outstanding efforts in adjusting the indexes with high accuracy.) For the wavelength $\lambda_{\rm o}$, the PO is strictly a normal field PO for all incident beams; placed in front of an objective, it will give for all stars a spectrum, in which the virtual $\lambda_{\rm o}$ line will be located where the direct image of the star would have been. If one rotates the prism 180 degrees around the optical axis of the objective, the spectrum will rotate around the line $\lambda_{\rm o}$ and a sideways shift of one spectrum, with respect to the other, will be representative of the radial velocity of the star. The RVs measured with this method are consistent for all the stars measured in a same field. The difference between these RV and those measured in the IAU standard is a constant. The Schwarzschild method (1913) can, therefore, be applied. The large field effects generated by ordinary prisms, which rendered the method impractical, have been corrected. For each star in the same field, we can write

d = C + kV

where d is the shift, V the RV in the IAU standard and C and k are constants. In principle, the knowledge of the RV in the standard system of one star in the field is sufficient to calibrate the whole field.


  \begin{figure} \par\includegraphics[width=5.7cm,clip]{cf10160fig02.eps} \end{figure} Figure 2: Histogram of $\epsilon $ for 20 SPO fields. $\epsilon = \sqrt {\Sigma (V-V')^{2} / N(N-1)}$ (kms-1 in abscissa. Number of stars in ordinate)

We have used two instruments:

1 -
The 15 cm diameter PO associated with an objective of 2 m focal length (PPO) (Fehrenbach 1951);
2 -
A 60 cm diameter PO associated with the 62/90/200 cm Schmidt telescope of the Observatoire de Haute Provence (SPO) (Fehrenbach & Burnage 1970).
These instruments allow us to measure the RV of all the stars of a field, up to a magnitude depending on the exposure time. A great number of hot stars were measured and posed an interesting problem at the time: we found that the percentage of variables was extremely high (Duflot et al. 1995b). It is commonly accepted, now, that these stars are mostly multiple systems.

Regarding the accuracy of our measurements, the C constant varies from one exposure to another, due to the motion of the earth, the variation of the index of the glasses with the temperature and also an eventual uneven guiding of the telescope during exposure. We use, for each field, N exposures (minimum 3) centred on the same star. Comparing the results obtained on the N plates, we deduce for each star a relative radial velocity V' and an external error $\epsilon $

$\displaystyle \epsilon = \sqrt{\Sigma (V-V')^{2} / N(N-1)}.$     (1)

The process is entirely described in Duflot & Fehrenbach (1955a, 1955b).

Figure 2 shows the distribution of external errors for 1704 stars of a series of SPO exposures. The maximum of the curve is at 3.60 kms-1; the curve corresponds to a Gaussian distribution of errors. The right wing corresponds to variable RV stars or to stars with blurry lines difficult to measure. For SPO, this error corresponds to 1 micron on the plate. In the case of PPO, the dispersion is larger, but the quality of the images is somewhat inferior; the result is approximately the same in accuracy.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig3.eps} \end{figure} Figure 3: a) RV from the PPO compared to RV from catalogues large circles represent good quality from both sources small circles represent poor quality from one source points, poor quality from both


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{cf10160fig03bis.eps} \end{figure} Figure 3: b) RV from the SPO, compared to RV from catalogues large circles represent good quality from both sources small circles represent poor quality from one source points, poor quality from both

Figure 3 shows a plot of RV measured with the PO technique versus RVfrom catalogues, for 410 stars belonging to a series of fields measured with the PPO. The mean of the differences is +0.2 kms-1 and the standard deviation is 3.6 kms-1. Figure 3 shows the same relation for 247 stars belonging to the SPO. The mean of the differences is -0.2 kms-1 and the standard deviation is 3.6 kms-1, if 43 stars of lesser quality are not taken into account. For all stars, the mean difference is +0.7 kms-1, and the standard deviation is 3.7 kms-1.

3 Determination of the solar Apex by means of normal field PO

We have divided the stars in two spectral type groups: those ranging from B5 to F5 (group A) and those ranging from F6 to K8 (group K). We constructed the RV histogram for each field for both groups. Figure 4 shows these histograms for 6 PPO fields. It is clear that the RV dispersion is larger than the dispersion due to the measurement error; this represents the actual dispersion of RV in the fields. The measurement error, approximately 4 kms-1, can be neglected if we compare it to the dispersion of RVs. The position of the maximum on the RV axis, $V_{\rm g}$, is only affected by the final overall calibration of the field in the IAU system (2 to 3 km s-1) (Duflot et al. 1995b). When the number of stars in the field is too small to construct a histogram, we use the mean of the RVs of all the stars. Again, when the number of stars is greater than 10, this mean value is not affected by the measurement errors. We conclude from this study that our material is homogeneous, and well-suited to the study of the solar apex.


  \begin{figure} \par\includegraphics[width=11cm,clip]{cf10160fig04.eps} \end{figure} Figure 4: Histograms for 6 PPO fields, B5 to F5 spectra. In the frame: field name. $N_{\rm o}$, $V_{\rm o}$, $\Sigma $ of Gauss repartition. $N=N_{\rm o} \exp-((V-V_{\rm o})/ \Sigma)^{2}$. In abscissa, interval = 10 kms-1. In ordinate, interval = 10 (number)

As a first approach, we used the RVs obtained with the PPO in 246 fields (Fehrenbach et al. 1987c, 1989, 1996, 1997), (Duflot et al. 1990, 1992, 1995a). We then added the RVs obtained with the SPO (Fehrenbach & Burnage 1981, 1982, 1990), (Fehrenbach et al. 1984, 1987a, 1987b, 1992). Altogether, this represents a sample of 11978 stars. The results of both studies are consistent.


   
Table 1: Data from PPO study


      AK AK AK' AK' A A K K
N$^{\circ}$ field AR D N VR N VR N VR N VR
1 38 94.43 38.55 22 -2.0 20 -2.4 13 -4.2 7 1.1
2 44 7.50 44.35 22 -9.4 18 -10.6 14 -11.4 4 -7.8
3 45.1 40.30 45.64 22 0.4 20 -0.1 14 -2.0 6 4.5
4 45.2 42.62 45.76 21 -4.9 19 -3.4 12 -2.6 7 -4.9
5 48.1 90.88 48.71 16 -3.9 14 -3.9 10 0.7 4 -15.3
6 48.2 3.47 48.64 15 -2.0 13 -1.2 10 -2.0 3 1.3


365

 U2 304.41 40.20 23 -9.2 19 -7.8 16 -8.7 3 -3
366 U3 305.80 40.33 22 -10.1 20 -9.4 17 -8.3 3 -15.7


Number of fields

 366 366 366 364
Number of stars 6965 6007 4138 1869
Number of stars per field 19.0 16.4 11.3 5.1
Mean of RV all fields   -5.0   -4.7   -4.2   -5.2

N    number of stars in the field.
AK  number of stars B5 to K8.
AK' number of stars B5 to K8, great RV discarded.
A     number of stars B5 to F5.
K    number of stars F6 to K8.

4 Study with PPO measurements

Some overcrowded fields were split. The 6965 stars were divided into 366 fields. A sample is given in Table 1. The magnitude of the stars ranges from 7 to 10. The coordinates of the 366 fields are given in Fig. 5; their declinations range from 0 to 75 degrees.


  \begin{figure} \par\includegraphics[width=10cm,clip]{cf10160fig05.eps} \end{figure} Figure 5: Position of PPO fields $-180^\circ $ to $+180^\circ $ in AR $0^\circ $ to $+90^\circ $ in $\delta $

To avoid the effect of high RVs on the mean $V_{\rm m}$, we discarded the few stars situated far in the wings of the RV distribution. Table 1 gives the number of stars used in this first study. An estimate of components of the Apex vector, U, V, W and S was computed (Table 2) with the classical method (Mihalas 1981). We then computed the theoretical velocity of the Sun in the direction of each field using these values, and determined the difference from the observed value. We minimised the sum of the squares of these differences by varying U, V and W. After a few iterations, we reach a final result which is very near to the original values. We did not actually use a sum of the squares, but rather the sum of the absolute values of the differences (the weight of discrepant values is of less importance). The results are shown in Table 3. We have made the computations taking into account the number of stars N contained in each field, by giving a weight equal to N, square root of N rounded to the nearest integer, and finally 1 to the contribution of each field. The three results are very similar.


   
Table 2: Coefficients of classical equations


Ch

 N $V_{\rm m}$ AR D A B C P D E F Q G H I R
I1 26 -21.7 22.46 61.86 0.19 0.08 0.38 9.46 0.08 0.03 0.16 3.91 0.38 0.16 0.78 19.1
I2 23 -17.1 24.96 61.15 0.18 0.09 0.38 7.31 0.09 0.04 0.18 3.40 0.38 0.18 0.78 15.1
J1 22 -22.0 27.23 60.99 0.18 0.09 0.38 9.44 0.09 0.05 0.19 4.86 0.38 0.19 0.77 19.3
J2 15 -8.5 28.85 57.94 0.18 0.10 0.37 3.61 0.10 0.05 0.20 1.99 0.37 0.20 0.76 7.4


P1

 17 -22.5 302.83 38.17 0.18 -0.28 0.26 9.59 -0.28 0.44 -0.41 -14.87 0.26 -0.41 0.38 13.9
P3 20 -13.3 304.50 38.15 0.20 -0.29 0.28 5.92 -0.29 0.42 -0.40 -8.62 0.28 -0.40 0.38 8.2
P4 18 -11.3 305.28 38.20 0.21 -0.29 0.28 5.13 -0.29 0.41 -0.40 -7.25 0.28 -0.40 0.38 7.0
Sum 21.48 -2.01 19.39 400.1 -2.01 27.47 7.05 -287.2 19.39 7.05 42.06 572.1

$U^{\star}\Sigma A + V^{\star}\Sigma B + W^{\star}\Sigma C = \Sigma P$
$U^{\star}\Sigma D + V^{\star}\Sigma E + W^{\star}\Sigma F = \Sigma Q$
$U^{\star}\Sigma G + V ^{\star}\Sigma H + W ^{\star}\Sigma I = \Sigma R$

  $A = c1^{\star}c1 $ $D = c2^{\star}c1$ $G = c3^{\star}c1$
  $B = c1^{\star}c2$ $E = c2^{\star}c2$ $H = c3^{\star}c2$
  $C = c1^{\star}c3$ $F = c2^{\star}c3$ $I = c3^{\star}c3$
  $P = -c1^{\star}V_{\rm m}$ $Q = -c2^{\star}V_{\rm m}$ $R = -c3^{\star}V_{\rm m}$

$c1 = \cos D^{\star}$ cos AR
$c2 = \cos D^{\star}$ sin AR
$c3 = \sin~D$

This table is also valid if AR and D are changed into LII, BII.


The results obtained are:

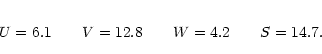
\begin{eqnarray*}U = 6.1 \qquad V = 12.8 \qquad W = 4.2 \qquad S = 14.7. \end{eqnarray*}


They are quite different from those usually obtained:

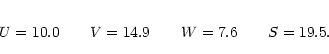
\begin{eqnarray*}U = 10.0 \qquad V = 14.9 \qquad W = 7.6 \qquad S = 19.5. \end{eqnarray*}


We can argue that the latter values are usually derived from the RVs found in the Wilson Catalogue for stars brighter than magnitude 6 or stars measured because of their individual interest. Our sample is made of much fainter stars, all spectral types are represented and all observable stars in the field are included, thus, there are no observational biases.


  \begin{figure} \par\includegraphics[width=10cm,clip]{fig6.eps} \end{figure} Figure 6: Differences between the observed velocity $V_{\rm m}$ and the velocity V derived from our results (PPO). - negative difference, $\mid $ positive difference


  \begin{figure} \par\includegraphics[width=10cm,clip]{fig7.eps} \end{figure} Figure 7: Differences between the observed velocity $V_{\rm m}$ and the velocity V derived from our results (PPO+SPO). Average of computed differences for large regions


   
Table 3: Results of U, V, W, S using PPO measurements


  U V W S
N A to K' 6.07 12.80 4.33 14.82
one A to K' 6.24 12.77 4.03 14.77
rac A to K' 6.09 12.76 4.15 14.74
mean   6.13 12.78 4.17 14.77


N

 A 5.87 12.05 3.59 13.88
one A 5.78 11.81 4.14 13.78
rac A 5.62 11.78 4.22 13.71
mean   5.76 11.88 3.98 13.79


N

 K 6.45 14.54 5.28 16.76
one K 6.37 13.81 4.84 15.96
rac K 6.27 14.17 5.14 16.32
mean   6.37 14.17 5.09 16.35


Adopted values
rac A to K' 6.09 12.76 4.15 14.74
rac A 5.62 11.78 4.22 13.71
rac K 6.27 14.17 5.14 16.32

N: weight equal to N. number of stars in the field.
one: weight 1 to the contribution of each field.
rac: weight equal to the square root of N.

We computed, for the 366 fields, the difference between the observed velocity $V_{\rm m}$, and the velocity V derived from our estimation of the solar apex. The average of these differences is 0.6 kms-1 $\pm$ 0.003, with a standard deviation of 8 kms-1. This justifies our choice of an expansion factor K equal to 0. The positive and negative differences are evenly scattered (Fig. 6). We calculated the average of the differences for large regions; Fig. 7 shows that there is no systematic effect, which is usually small except for one region containing only 6 fields.


  \begin{figure} \par\includegraphics[width=10cm,clip]{cf10160fig08.eps} \end{figure} Figure 8: Position of PPO+SPO fields $-180^\circ $ to $+180^\circ $ in AR $0^\circ $ to $+90^\circ $ in $\delta $

5 Determination of the solar apex with PPO and SPO

Figure 8 shows the distribution of the fields on the celestial sphere. Altogether, the number of stars considered is 11 978 divided into 576 fields containing an average of 20 stars each; the magnitudes range from 7 to 11. Table 4 gives the results of the computation. The values are corrected for galactic rotation as discussed below; they confirm the results of Table 3:
PPO U = 6.1 V = 12.8 W = 4.2
SPO + PPO U = 5.4 V = 13.4 W = 4.2.


 

 
Table 4: Results of U, V, W, S using PPO+ SPO measurements


  U V W S
" $-90^\circ<{\rm BII}<90^\circ$"  
rac A to K' 5.38 13.45 4.22 15.09
rac A 4.02 12.59 5.01 14.13
rac K 7.31 13.93 4.24 16.29


" $-45^\circ<{\rm BII}<45^\circ$"

  
rac A to K' 4.85 13.34 3.33 14.59
rac A 3.89 12.88 4.31 14.13
rac K 7.00 13.70 3.41 15.77


Standard

   10.0 14.9 7.6 19.5
Basic   8.9 11.0 6.0 15.4


6 Determination of the solar apex taking into account the distance of the stars

Instead of using magnitude for grouping the stars, we estimated their distances. Except for a few PPO fields, we do not have information on luminosity classes. We then assumed that all stars were of luminosity class V; the estimation was performed using the photographic distance modulus m - M. We divided the stars into four series: stars with 0< D <100 parsecs, 100< D<300parsecs, 300< D < 500 parsecs and D >500 parsecs. For each series, we computed, field by field, the mean RV and corrected for the galactic rotation. We adopted an Oort constant of 15 kms-1kpc-1 and the correction is, according to Lang (1980)

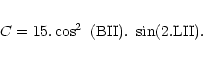
\begin{eqnarray*}C = 15. \cos^{2}~({\rm BII}). ~\sin(2.{\rm LII}). \end{eqnarray*}


The correction seems to be small, compared to the measurement errors, but is important due to its systematic nature.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{cf10160fig09.eps} \end{figure} Figure 9: Study taking into account the distance of the stars. Distribution of the fields in LII, BII. $-45^\circ < {\rm BII} < +45^\circ $ PPO Filled circles, SPO open circles

We discarded a few stars whose distance determinations were unreliable. Table 5 gives the number of fields and the number of stars per field. Figure 9 shows the distribution in LII, BII for $45^\circ <{\rm BII}<+45^\circ$. There are only a few stars in the series of stars with D>500 parsecs and some fields contain only 4 to 7 stars. The computation was performed exactly the same way as for the previous study. Table 6 gives U, V, W and S for stars $-45^\circ < {\rm BII} < +45^\circ $. Table 7 gives the values obtained when all stars are taken into account. The final results are those obtained with a weighting by square root of N (rac).


 

 
Table 5: Number of fields and stars per field in the study taking into account the distance of the stars


" $-90^\circ<{\rm BII}<90^\circ$"

    
  <100 pc 100 to 300 pc 300 to 500 pc > 500 pc Total
N fields 571 570 515 351 576
N stars 4444 3546 2346 1850 12 186
mean D 47 192 378 945  


" $-45^\circ<{\rm BII}<45^\circ$"

    
  <100 pc 100 to 300 pc 300 to 500 pc > 500 pc Total
N fields 517 516 484 339 522
N stars 3869 3265 2280 1823 11 237
mean D 46 195 378 948  



 

 
Table 6: Results of U, V, W, S in the study taking into account the distance of the stars for $-45^\circ < {\rm BII} < +45^\circ $. one, rac, N: Weights, see Table 3. The numbers under U, V, W, S are an indication of the accuracy of this values
        one       rac     N    
                           
D $\bar{D}$ U V W S U V W S U V W S
<100 46 8.75 13.34 2.96 16.23 9.79 13.20 3.25 16.75 10.00 13.00 3.36 16.74
    0.6 0.5 1.1   0.5 0.5 0.9   0.5 0.5 0.9  
                           
100 to 300 195 7.44 11.70 6.31 15.23 8.24 11.58 5.97 15.42 8.47 11.42 6.12 15.48
    0.6 0.6 1.3   0.6 0.6 1.1   0.6 0.5 1.0  
                           
300 to 500 378 2.98 10.44 5.43 12.14 2.93 10.36 4.79 11.78 2.90 10.38 4.41 11.64
    0.6 0.6 1.3   0.6 0.6 1.2   0.6 0.5 1.2  
                           
>500 948 8.34 13.16 5.67 16.58 8.57 11.57 5.97 15.59 8.38 10.96 7.38 15.65
pc pc 0.8 1.0 2.2   0.7 0.9 1.6   0.7 0.8 2.6  



 

 
Table 7: Results of U, V, W, S in the study taking into account the distance of the stars for $-90^\circ < {\rm BII} < +90^\circ $one, rac, N: Weights, see Table 3. The numbers under U, V, W, S are an indication of the accuracy of this values


      one       rac     N    
                           
D $\bar{D}$ U V W S U V W S U V W S
<100 47 8.63 13.41 3.86 16.41 9.60 13.25 4.26 16.91 9.78 13.10 4.40 16.93
    0.8 0.7 1.1   0.7 0.6 0.9   0.6 0.6 0.8  
                           
100 to 300 192 7.52 11.95 6.72 15.64 8.30 11.65 6.50 15.71 8.51 11.66 6.86 15.98
    0.8 0.7 1.2   0.8 0.7 1.1   0.8 0.7 1.1  
                           
300 to 500 378 3.39 10.43 4.81 11.98 3.21 10.33 4.67 11.78 3.29 10.48 4.90 12.03
    0.8 0.8 1.5   0.8 0.8 1.5   0.9 0.8 1.5  
                           
>500 945 8.46 13.31 6.21 16.95 8.58 11.68 6.30 15.80 8.28 10.96 7.11 15.47
pc pc 0.8 1.0 2.2   0.9 1.1 2.0   0.9 1.0 2.5  



  \begin{figure}% latex2html id marker 506\par\includegraphics[width=8.8cm,clip]... ...PO Table~\ref{tab4} & & 4.85 & 13.34 & 3.33 & 14.59\\ \end{tabular}\end{figure} Figure 10: Variation of U, V, W, S as a function of the distance $-45^\circ < {\rm BII} < +45^\circ $.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{cf10160fig11.eps} \par\b... ...\\ $>$ 500 & 951 & 8.58 & 11.68 & 6.30 & 15.80\\ \end{tabular}\par\end{figure} Figure 11: Variation of U, V, W, S as a function of distance $-90^\circ < {\rm BII} < +90^\circ $.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{cf10160fig12.eps} \end{figure} Figure 12: Differences between the observed velocity $V_{\rm m}$, and the velocity V derived from our results, for distances less than 100 parsecs. LII in abscissa


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{cf10160fig13.eps} \end{figure} Figure 13: Number of differences between the observed velocity $V_{\rm m}$, and the velocity V derived from our results, for distances shorter than 100 parsecs. Intervals of 10 kms-1

Figures 10 and 11 show the variation of U, V, W and S with respect to distance, which is linear up to 500 pc, and their equations. We can consider that W is constant, independent of D, and equal to 4.9 kms-1. The results for D>500 pc are irrelevant due to the inaccuracy of the data; there are only a few fields, containing very few stars.

Figures 12 and 13 show the differences between the values of RV computed from our values of U, V, W and those derived from observation, for distances less than 100 parsecs. The differences are not due to measurement errors, but to the scatter in RV. We note no variation with LII. Their distribution is Gaussian; 50% of the differences are smaller than 14.3 kms-1.

An interpretation of these results is not easy. We note the small variation in W, perpendicular to the galactic plane. It is U which varies the most. Our values differ from conventional values, but should be compared with those recently computed with the Hipparcos data.


 

 
Table 8: Comparison with other publications


  U V W S  
Standard   10.04 14.88 7.62 19.50  
Basic   8.92 11.02 6.02 15.40  


Delhaye

 1965 stand 10.4 14.8 7.3 19.5  
Delhaye 1965 basic 9.0 11.0 6.0 15.4  


Jascheck

 1991 Mean 11.4 14.7 7.6 20.1  
Jascheck 1992 Median 9.8 11.6 5.9 16.3  
Jascheck 1992 Mode 8.6 7.2 3.8 11.8  


Mayor

 1974 10.3 6.3 5.9 13.4  


Dehnen

 1998 10.0 5.3 7.2 13.4  


Mignard

 1999 11.0 10.87 7.23 17.10 A0-F5
"   9.88 14.19 7.76 18.95 K0-K5


Fehrenbach et al.

   9.79 13.20 3.25 16.75 $\bar{D}$ = 46 pc
"   8.24 11.58 5.97 15.42 $\bar{D} = 195$ pc
"   2.93 10.36 4.79 11.78 $\bar{D} = 378$ pc


7 Comparison with other publications

Table 8 shows the results published in the literature. These results have been computed from RV or proper motions and distances found in the literature, or computed from Hipparcos data. There is an astonishing discrepancy in the results. Ours were obtained from a homogeneous sample of more than 11 000 stars of all spectral types evenly scattered over the northern hemisphere. The photographic magnitude of this sample ranges from 7 to 11. This sample has no equivalent in the literature.

Acknowledgements
We wish to thank the technical and administrative staff of the Observatoire de Haute-Provence and Observatoire de Marseille who strongly helped in the design of observing and measuring instrumentation, and in the reduction of data. We particularly thank our assistants who have so closely participated to the measurements of some 40 000 RV. We very warmly thank L. Prévot and M. Mayor who agreed to measure RV specially for us when no known RV was available to calibrate our fields.

References

 
Copyright ESO 2001