Appendix A: Formulae in the linear approximation

In the absence of a non-axisymmetric perturbation, the orbits can be computed in the epicyclic approximation, and the variables $\xi$, $\eta$ << r₀ follow the evolution of an harmonic oscillator, with the epicyclic frequency $\kappa$. In the presence of a bar perturbation, the equations of motions, in the reference frame rotating with the perturbation at $\Omega_{\rm p}$ are (Lindblad & Lindblad 1994):

$$\ddot{\xi} - 2\Omega\dot{\eta} - 4\Omega A\xi = {{{\rm d}\Phi_2}\over{{\rm d}r}} \cos{2\theta} = C \cos{2\theta }$$

$$\ddot{\eta} + 2\Omega\dot{\xi} = -2{{\Phi_2}\over{r}} \sin{2\theta} = -D \sin{2\theta }$$

where A is the Oort constant:

$$A = -\frac{1}{2}r\frac{{\rm d}\Omega}{{\rm d}r},$$

related to the epicyclic frequency $\kappa$ by:

$$\kappa^2 = 4\Omega^2 -4\Omega A .$$

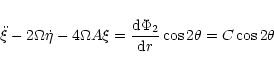
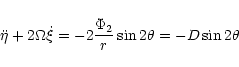
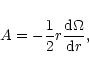
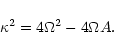
The oscillator is now forced by an external perturbation at the imposed frequency $\omega = 2(\Omega-\Omega_{\rm p})$.

Taking for $\xi$ and $\eta$ a solution of the form:

$$\xi = a \cos {(2\theta + 2\psi)} + c\, {\rm e}^{-\lambda t} \cos{(\kappa' t +\phi_0)}$$

$$\eta = b \sin {(2\theta + 2\psi)} + c'\, {\rm e}^{-\lambda t} \cos{(\kappa' t +\phi_0)}$$

with the same phase angle $\psi$ ($\xi$ and $\eta$ in quadrature), and $\kappa'$ the modified proper frequency of the damped oscillations, it can be found that:

$$a = {{\frac{{\rm d}\Phi_2}{{\rm d}r} + 4 \frac{\Omega}{\omega... ...}{r}}\over {\sqrt{(\kappa^2-\omega^2)^2+4\omega^2\lambda^2}}}$$

and

$$\tan 2 \psi = -{{2 \omega\lambda}\over{\kappa^2-\omega^2}}$$

with

$$\omega^2 b = D -2\Omega\omega a.$$

The damped terms, exponentially decreasing with $\lambda t$, correspond to the epicycles around the guiding centers, and are not considered here (only through the velocity dispersion).

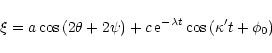
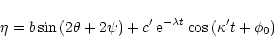
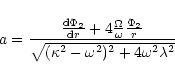
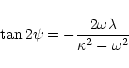
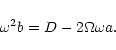
Acknowledgements

We wish to thank Jean-Gabriel Cuby and Claire Moutou for their help and support during the ISAAC observations. We also wish to thank the referee, Alan Morwood, for a detailed and critical reading of the manuscript. This work has been supported by the Swiss National Science Foundation.