Online Material

Appendix A:

The ${\beta }$ parameter (Eq. 3) is defined by the luminosity ratio $L_{\rm h}/L_{\rm g}$ and the giant radius in units of the separation of the components, $R_{\rm g}/A$. To determine these quantities we used published parameters and/or made appropriate estimates. If applicable, we used spectral types of the cool components in symbiotic binaries of Mürset & Schmid (1999) and empirically determined dependencies of effective temperature and linear radius upon the spectral type given by van Belle et al. (1999). Table 4 summarizes the resulting parameters. Their uncertainties represent mean square errors of the mean value given by Eq. (3). A brief explanation to Table 4 is given below for individual objects.
AXPer: Skopal (1994) determined $R_{\rm g}/A = 0.28 \pm 0.01$. The luminosity of the giant, $L_{\rm g} = 1\,250 \pm 400~L_{\odot}$ for the distance $d = 1\,730 \pm 230$pc (Skopal 2000). The hot star luminosity, $L_{\rm h} = 314 \pm 84~L_{\odot} (d/1730\,pc)^{2}$ (Mürset et al. 1991) with the uncertainty resulting from that of d.
BFCyg: Parameters $R_{\rm g}/A = 0.54 \pm 0.02$ and $L_{\rm h}/L_{\rm g} \approx 1.4$ (Skopal et al. 1997). The uncertainty of the luminosity ratio is $\sim$30%, which is relevant to its determination from the observed fluxes.
CICyg: Kenyon et al. (1991) estimated $R_{\rm g}/A = 0.38 \pm 0.02$. Adopting their estimate of the total mass of the binary, $M_{\rm T} = 1.9 \pm 0.6~M_{\odot}$, we get A = $470 \pm 50~R_{\odot}$ for $P_{\rm orb}$ = 855.25 days (Aller 1954), which yields $R_{\rm g} = 179 \pm 20~ R_{\odot}$. The spectral type (ST) of the red giant in CICyg, M5.5, corresponds to its effective temperature, $T_{\rm eff} = 3\,400 \pm 30$K, which then yields $L_{\rm g} = 3\,830 \pm 990~L_{\odot}$. Finally, Mürset et al. (1991) determined $L_{\rm h} = 560~L_{\odot}$(d/1.5kpc)².
EGAnd: From the contact times of a minimum observed in continuum fluxes at $\lambda$1320Å (Pereira 1996) we determined $R_{\rm g}/A = 0.32 \pm 0.05$ for the orbital period, $P_{\rm orb}$ = 482 days (Skopal 1997) and a circular orbit. As the minimum is caused by Rayleigh scattering of the hot star radiation on the neutral atoms of the cool giant wind, this is an upper limit. The luminosity ratio for the two stars, $L_{\rm h}/L_{\rm g} \approx 1/60$ (Vogel et al. 1992). The uncertainty of this ratio is assumed to be of 30%.
AGDra: From the energy distribution in the spectrum during quiescence (Greiner et al. 1997) we estimated the observed fluxes $F^{\rm obs}_{\rm g} = 9.5 \pm 2.0 \; 10^{-9}$ and $F^{\rm obs}_{\rm h} = 1.3 \pm 2.0 \; 10^{-8}$ergcm^-2s^-1, i.e. $L_{\rm h}/L_{\rm g} = 1.3 \pm 0.3$. Smith et al. (1996) estimated the surface gravity as $\log(g) = 1.6 \pm 0.3$ (g in units of cms^-2), which for the cool component mass of 1.5 $M_{\odot}$ (Mikolajewska et al. 1995), yields $R_{\rm g} = 32 \pm 11~R_{\odot}$. This value is also consistent with that corresponding to the recent $ST/T_{\rm eff}$ dependencies. For $M_{\rm T} = 2~M_{\odot}$ and $P_{\rm orb}$ = 550 days (Gális et al. 1999) we have $A = 356~R_{\odot}$ and thus $R_{\rm g}/A = 0.09 \pm 0.03$. We can also estimate the distance to AGDra $d = 980 \pm 200$pc from $L_{\rm g} = 285 \pm 100~ L_{\odot}$ ( $T_{\rm eff} = 4\,200\,\rm K$ as for K3-4III giant) and $F^{\rm obs}_{\rm g}$.
V1329Cyg: The maximum width of the pre-outburst eclipses (Fig. 1 of Schild & Schmid 1997),

 

 

Table A.1: The ${\beta }$ parameter characterizing the reflection effect

Object	$L_{\rm h}/L_{\rm g}$	$R_{\rm g}/A$	${\beta }$
AXPer	$0.25\pm 0.10$	$0.28\pm 0.01$	$0.020\pm 0.008$
BFCyg	$1.4\pm 0.4$	$0.54\pm 0.02$	$0.40\pm 0.12$
CICyg	$0.15\pm 0.06$	$0.38\pm 0.02$	$0.06\pm0.01$
EGAnd	$0.017\pm0.005$	$\le 0.32\pm0.05$	$\le 0.002\pm0.001$
AGDra	$1.3\pm0.3$	$0.09\pm 0.03$	$0.01\pm0.008$
V1329Cyg	3.1-1.2	<0.39	0.18 - 0.47
He2-467	$\approx$60	0.05-0.03	0.07 - 0.2
ZAnd	1	$0.24\pm0.05$
V443Her	$\sim$0.7	$\sim$0.26	$\sim$0.04
AGPeg	$\sim$1	$\sim$0.17	$\sim$0.03

t₄ - t₁ = 0.129 $P_{\rm orb}$, yields the upper limit of $R_{\rm g}/A$ = 0.39 (assuming the radius of the eclipsed object to be negligible) for $P_{\rm orb}$ = 958 days (Schild & Schmid 1997). Mürset et al. (1991) derived $L_{\rm h} = 9\,500~L_{\odot}$. The ST of the giant in V1329Cyg, M6, corresponds to $T_{\rm eff} = 3\,375 \pm 100$K. A reasonable range of $M_{\rm T} = 1 - 4~M_{\odot}$ (elements of the spectroscopic orbit are not available) gives the range of $A = 410 - 650\,R_{\odot}$, consequently $R_{\rm g} = 160 - 260~R_{\odot}$ and $L_{\rm g} = 3\,100 - 7\,800~L_{\odot}$. Thus for V1329Cyg we can estimate only a range of the ${\beta }$ parameter.
He2-467: From the energy distribution in the spectrum (Munari & Buson 1992) we estimated the luminosity ratio $L_{\rm h}/L_{\rm g} \approx 60$ (assuming that the observed nebular component is equal to $\int_{0}^{912}F_{\rm h}(\lambda)\,{\rm d}\lambda$), and particularly $F^{\rm obs}_{\rm g} = 6.3 \pm 2.0 \; 10^{-10}$ergcm^-2s^-1, which gives $L_{\rm g} = 78 \pm 20~L_{\odot}$. This value is in a very good agreement with the $ST/T_{\rm eff}/R$ dependencies (ST = K0III: $T_{\rm eff} = 4\,513 \pm 100$K, $R_{\rm g} = 14 \pm 3~R_{\odot}$ that implies $L_{\rm g} = 73 \pm 25~L_{\odot}$). To estimate the separation A, we assume a typical range of $M_{\rm T} = 1 - 4~M_{\odot}$, which for $P_{\rm orb} = 478.5$ days (Arkhipova et al. 1995) corresponds to the range of $A = 257 - 408~R_{\odot}$.
ZAnd: For the spectral type of the giant in ZAnd, M4.5III, the $ST/T_{\rm eff}/R$ and V-K/R dependencies suggest $T_{\rm eff}$ = 3425K, $R_{\rm g} = 100\pm 20~R_{\odot}$ implying $L_{\rm g} = 1\,230~L_{\odot}$. We used the V-K = 5.4 (Kamath & Ashok 1999, Fig. 1, E_B-V = 0.3). According to Schmid & Schild (1997) $M_{\rm T} = 1.8~M_{\odot}$, which for $P_{\rm orb}$ = 758.8 days (Mikolajewska & Kenyon 1996) yields $A = 420~ R_{\odot}$, and Mürset et al (1991) derived $L_{\rm h} = 700 \pm 50~L_{\odot}~(d/1.2\,kpc)^{2}$. So in ZAnd we have $R_{\rm g}/A = 0.24 \pm 0.05$ and for the range of possible distances (0.98 - 1.6kpc, Mürset et al. 1991). This luminosity ratio is also supported by the energy distribution in the spectrum of ZAnd (e.g. Nussbaumer & Vogel 1989).
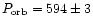V443Her: Only rough estimates of fundamental parameters are available in the literature: $L_{\rm g} \sim 1\,500~L_{\odot}$, $L_{\rm h} \sim 1\,000~L_{\odot}$, $R_{\rm g} \sim 110~R_{\odot}$, $M_{\rm T} \sim 2.9~M_{\odot}$ (Dobrzycka et al. 1993). For $P_{\rm orb} = 594\pm 3$ days (Kolotilov et al. 1995) we get $A \sim 424~R_{\odot}$.
AGPeg: Kenyon et al. (1993) estimated $L_{\rm g} \sim 1\,150~L_{\odot}\,(d/0.8\,kpc)^{2}$ and Mürset et al. (1991) determined $L_{\rm h} \sim 1\,000~L_{\odot}\,(d/0.8\,kpc)^{2}$, i.e. $L_{\rm h}/L_{\rm g} \sim 1$. The $ST/T_{\rm eff}/R$ dependencies suggest $T_{\rm eff}$ = 3425K, which corresponds to $R_{\rm g} \sim 89~R_{\odot}(d/0.8\,kpc)^{2}$, and $M_{\rm T} \sim 3.1~M_{\odot}$ (Kenyon et al. 1993) implies $A \sim 530~R_{\odot}$ ( $P_{\rm orb}$ = 812.6 days, Skopal 1998a), and thus $R_{\rm g}/A \sim 0.17$.

Appendix B:

Here we investigate the suggested connection between the parameters a and X (Sect. 4.2). STB derived the parameter X as

$$X=\frac{4\pi\mu^{2}m_{\rm H}^{2}}{\alpha_B}A L_{\rm ph} \Big(\frac{v_{\infty}}{\dot M}\Big)^{2}.$$ (B.1)

The meaning of individual parameters is noted in the text above. Unfortunately, there are only a few symbiotic objects for which the parameter X can be satisfactorily determined. In Table 5 we summarize the average values of parameters $\dot M$ in $10^{-7}~M_{\odot}$ yr^-1, $L_{\rm ph}$ in $10^{46}\,\rm photons\,s^{-1}$ (Eq. (11)), a (Eq. (4), Table 1) and X. Other auxiliary parameters as in Appendix A and in Mürset et al. (1991), if not referred to otherwise. In all cases $v_{\infty} = 30\,\rm km\,s^{-1}$.

Figure B.1: A correlation between the shape of the LC characterized by the parameter a (Sect. 3.2) and the extent of the symbiotic nebula given by the parameter X

 

 

Table B.1: Parameters a and X for selected objects

Object	$\dot M$	Ref.	$L_{\rm ph}$	a	X
AGPeg	2.0		7.2	0.50	>15
ZAnd	2.0	1	3.5	0.53	$\approx$14
AGDra	2.0	2	2.6	0.50	11
V1329Cyg	15		56	0.50	$\sim$8
BFCyg	$\approx$20		50	0.57	$\approx$3
CICyg	>4		3.7	0.83	<5
AXPer	$\sim$10	3	2.2	0.70	$\sim$0.4
EGAnd	2.0	4	0.077	1.0	0.3

Ref.: 1 - Fernández-Castro et al. (1988), 2 - Mikolajewska et al. (1995),
3 - Skopal et al. (in press), 4 - Vogel (1991): this value is needed to explain the nebular continuum.
In contrast, the value of 3-4 $\, 10^{-8}~M_{\odot}$ yr^-1 suggested by effects of the Rayleigh scattering in the far UV continuum leads to X = 7.

The main obstacle to determining the X parameter results from its strong dependence on $\dot M$, which is very poorly known at present. The situation is difficult mainly in cases with small values of the parameter X, a little change in which produces a large change in the extent of the nebula. In addition, intrinsic variation in $\dot M$ and/or $L_{\rm ph}$ are often observed. For example, a variable column density of hydrogen atoms during different cycles of BFCyg (Fernandez-Castro et al. 1990) suggests a variability in the geometry of the Hii zone. Also the case of EGAnd is disputable (see Table 5) and for CICyg there is no detailed analysis of its current quiescent phase. In the latter case, possible values of $\dot M$ = $10^{-6}~M_{\odot}$ yr^-1 and $v_{\infty} = 20\,\rm km\,s^{-1}$ result in X << 1 in contrast to its upper limit of 5 (Table 5). Therefore we adopted X = 1 for CICyg. On the other hand, all cases with very large X ( , AGPeg, ZAnd, AGDra,V1329Cyg) show a simple sinusoidal shape ( $a \sim 0.5$).

In spite of these problems the present knowledge of the fundamental parameters of symbiotic binaries makes a correlation between a and X possible (Fig. 5). However, further investigation is needed to determine more accurate parameters, mainly the mass-loss rate via the wind from cool giants in binaries, to verify the relationship between the profile of the LC and the extent of the symbiotic nebula.

Appendix C:

In this appendix we introduce a modification of the STB model accounting for the additional ionizations due to the inflow of neutral material into the ionized region through the ionization front due to the orbital motion and the velocity of the giant wind.

Figure C.1: The Hi/Hii boundary given by the STB model (dashed line) and its modification due to the orbital motion (solid line). Our model (Eq. C.1) was calculated for $P_{\rm orb}$ = 757 days, $A = 465~R_{\odot}$ and the mass ratio q = 6. The binary rotates anti-clockwise

At a boundary point, $r_{\rm b}$, the rate of particles, $n(r_{\rm b})v_{\perp}$, crosses the area of the front, dS = d $\Omega\,r^{2}/\cos(\textbf{\textit{r}}{\bf S})$, where d$\Omega$ is a small angle around the vector r pointing to $r_{\rm b}$ from the hot star and $v_{\perp}$ is the velocity of atoms in the direction of S (i.e. perpendicular to the boundary at the point $r_{\rm b}$). Thus, within the Hii region, the rate of photons, $L_{\rm ph}$, capable of ionizing hydrogen, has to balance a surplus of $\alpha_{B}[n(r_{\rm b})v_{\perp}]^{2} {\rm d}S$ recombinations in addition to the steady state situation; $\alpha_{B}$ stands for the total hydrogenic recombination coefficient for case B. The distance $r_{\rm b}$ from the hot star of the modified ionization front is then given by the equilibrium condition

$$\frac{{\rm d}\Omega}{4\pi} L_{\rm ph}=\alpha_{B}\,{\rm d}\Ome... ...m d}r - \alpha_{B}\,n^{2}(r_{\rm b})v_{\perp}^{2} {\rm d}S.$$ (C.1)

The velocity component, $v_{\perp}$, is calculated from the velocity of a particle ${\bf v = v_{\rm wind} - \omega \times \textbf{\textit{r}}_{\rm G}}$ in the frame rotating with angular velocity $\omega = 2\pi/P_{\rm orb}$; $\bf\textbf{\textit{r}}_{\rm G}$ is the position vector with respect to the centre of mass of the system. Figure 6 shows a comparison of the closed boundary calculated according to Eq. (C.1) and that of the STB model.