A&A 365, 440-464 (2001)
DOI: 10.1051/0004-6361:20000072

The circumstellar environment of low-mass protostars: A millimeter continuum mapping survey

F. Motte^1,2 - P. André²

Send offprint request: F. Motte,

1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 - CEA, DSM, DAPNIA, Service d'Astrophysique, CE Saclay, 91191 Gif-sur-Yvette Cedex, France

Received 6 June 2000 / Accepted 5 September 2000

Abstract
We present a complete 1.3 mm continuum mapping survey of the embedded young stellar objects (YSOs) in the Taurus molecular cloud. We have also imaged several isolated Bok globules, as well as protostellar objects in the Perseus cluster. Our maps, taken with the IRAM 30 m telescope and the MPIfR bolometer arrays, are sensitive to the column density structure of the sources on spatial scales ranging from 1500-5000 AU to $>15\,000$ -50000 AU. For the protostellar envelopes mapped in Taurus, the results are roughly consistent with the predictions of the self-similar inside-out collapse model of Shu and collaborators. The envelopes observed in Bok globules are also qualitatively consistent with these predictions, providing the effects of magnetic pressure are included in the model. By contrast, the envelopes of Class 0 protostars in Perseus have finite radii $\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ } 10\,000$ AU and are a factor of 3 to 12 denser than is predicted by the standard model. In cluster-forming regions, individual protostellar collapse thus appears to be induced in compact condensations resembling more finite-sized Bonnor-Ebert condensations than singular isothermal spheres. Accordingly, the beginning of protostellar evolution is suggested to be more violent, with larger accretion rates, in protoclusters compared to regions of distributed star formation like Taurus. Follow-up line observations of the envelopes' velocity fields are required to confirm this suggestion. We also find that roughly half of the Class I infrared sources of Taurus are either at the very end of the main accretion phase or already in the pre-main sequence phase. These sources are surrounded by only remnant, finite-sized envelopes ( $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.01\ \mbox{$M_\odot$ }$ and $\mbox{$R_{\mbox{\tiny out}}$ }\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }1\,500$ AU). Lastly, our 1.3 mm continuum images reveal the presence of new candidate pre-stellar condensations and/or Class 0 protostars in the close environment of 8 Taurus Class I YSOs, 2 Bok globules, and 3 Perseus protostars.

Key words: stars: formation - stars: circumstellar matter - ISM: clouds - ISM: structure - ISM: dust

Author for correspondance: motte@submm.caltech.edu

1 Introduction: Testing the predictions
of collapse models

In the course of early stellar evolution, one expects progressive condensation of the circumstellar material surrounding young stellar objects (YSOs) from "cloud-core'' sizes ( $\sim$ $0.1\rm ~pc~\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ } 10\,000$ AU) to solar-system sizes ( $\sim$ 10-100 AU). Therefore, sensitive, high-angular-resolution maps of the circumstellar environment of YSOs such as those resulting from observations of optically thin dust continuum emission on large (sub)millimeter radiotelescopes, can potentially provide crucial tests of our theoretical ideas on star formation. In this paper, we present an extensive 1.3 mm continuum mapping study of a large sample of nearby protostellar dense cores in order to set constraints on their density structure. Below, we give a brief overview of existing collapse models and summarize the results of previous inconclusive observations.

In the "standard'' theory of spontaneous isolated star formation (e.g. Shu et al. 1987), low-mass stars form from dense cloud cores which have reached, in a quasi-static fashion, the $\rho (r) \propto r^{-2}$ density distribution of a singular isothermal spheroid (SIS) or toroid (cf. Li & Shu 1996, 1997). The collapse of such initially hydrostatic but unstable spheroids proceeds from the inside out, with production of a central "protostar'' surrounded by an infalling envelope (e.g. Shu et al. 1987). At any given time, the infall envelope is bounded by the front of a collapse expansion wave which propagates outward at the isothermal sound speed, $\mbox{$a_{\mbox{\tiny s}}$ }$ . Outside the time-dependent radius $r_0 = \mbox{$a_{\mbox{\tiny s}}$ }\, t$ of the infalling envelope, the cloud core is at rest and retains its initial $\rho (r) \propto r^{-2}$ density structure. Inside r₀, the material is nearly in free-fall and the density asymptotically approaches a $\rho(r) \propto r^{-1.5}$ power-law. This protostellar model starting from SIS initial conditions has been widely used in the past, partly because it is based on a relatively simple, semi-analytical similarity solution for the collapse (Shu 1977), allowing rotation and magnetic fields to be treated as perturbations (e.g. Terebey et al. 1984; Galli & Shu 1993).

Other collapse models exist that adopt different initial conditions. Whitworth & Summers (1985) have shown that there is a two-dimensional continuum of similarity solutions to the problem of isothermal spherical collapse. In this continuum, the well-known solutions proposed by Shu (1977) and Larson (1969), Penston (1969) represent two extreme limits. All isothermal similarity solutions share a universal evolutionary pattern. At early times (t < 0), a compression wave (initiated by, e.g., an external disturbance) propagates inward at the sound speed, leaving behind it a $\rho (r) \propto r^{-2}$ density profile. At t = 0, the compression wave reaches the center and a point mass forms which subsequently grows by accretion. At later times (t > 0), this wave is reflected into a rarefaction or expansion wave, propagating outward (also at the sound speed) through the infalling gas, and leaving behind it a free-fall $\rho(r) \propto r^{-1.5}$ density distribution. Several features of the standard model described above are thus in fact general. The various solutions can be distinguished by the absolute values of the density and velocity at $t \sim 0$ . In particular, the Shu (1977) solution has $\rho(r) = (\mbox{$a_{\mbox{\tiny s}}$ }^2/2\pi\,G)\ r^{-2}$ and is static (v = 0) at t = 0, while the Larson-Penston (1969) solution is $\sim$ 4.4 times denser and far from equilibrium ( $v \approx -3.3\ \mbox{$a_{\mbox{\tiny s}}$ }$ ). Apart from their simplicity, the great interest of these similarity solutions is that they represent asymptotes in various regimes of more complicated flows.

In practice, however, the initial conditions for fast protostellar collapse may not be self-similar and may involve a density profile that is flat at small radii (e.g. Ward-Thompson et al. 1994; André et al. 1996 - hereafter AWM96) and bounded or sharp-edged at some outer radius $\mbox{$R_{\mbox{\tiny out}}$ }$ (e.g. Motte et al. 1998 - hereafter MAN98; Bacmann et al. 2000) like a finite-sized Bonnor-Ebert isothermal sphere (e.g. Bonnor 1956). A number of recent numerical (magneto)hydrodynamic simulations or simplified analytical calculations attempt to describe the collapse in such a situation, either in the absence (e.g. Foster & Chevalier 1993; Henriksen et al. 1997 - HAB97; Masunaga et al. 1998) or in the presence (e.g. Tomisaka 1996; Basu 1997; Safier et al. 1997; Li 1998; Ciolek & Königl 1998) of magnetic fields. These studies find that supersonic infall velocities generally develop before point mass formation at t = 0. The Larson-Penston similarity solution is found to describe the collapse quite satisfactorily near t= 0 (at least for small radii), but the Shu solution is more adequate at intermediate $t \geq 0$ times, before the expansion wave reaches the edge of the initial, pre-collapse dense core.

In order to fully distinguish between collapse models, observations of both the density and the velocity profile of protostellar dense cores are in principle required. Since the density structure is much easier to measure, we focus on this type of observational constraints as a first step. Most previous relevant studies had only the spatial resolution to constrain the extreme outer parts of star-forming cloud cores (from $\sim$ $0.1\rm\ pc \sim 20\,000\$ AU to $\sim$ $1\$ pc - e.g., Loren et al. 1983; Cernicharo et al. 1985; Casali 1986; Davidson 1987; Yun & Clemens 1991 - hereafter YC91). On smaller spatial scales ( $\!\!\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }20\,000$ AU), only a few protostellar envelopes have been investigated in detail up to now (e.g., Walker et al. 1990; Ladd et al. 1991; Butner et al. 1991; Barsony & Chandler 1993; Chandler et al. 1998). These studies have yielded contradictory, inconclusive results, i.e., radial density profiles of the type $\rho(r)\propto r^{-p}$ with p ranging from 0.5 (e.g. Barsony & Chandler 1993) to 3 (e.g. YC91). A more comprehensive investigation on a broad, homogeneous sample of protostellar dense cores on spatial scales < 0.1 pc is thus clearly called for to make progress and draw more definite conclusions.

The present paper discusses the results of a systematic 1.3 mm dust continuum mapping investigation conducted at an angular resolution of $11\hbox{$^{\prime\prime}$ }$ with the IRAM 30 m telescope. These 1.3 mm observations probe the column density structure of protostellar envelopes on spatial scales from $r \sim 1\,500$ - $5\,000$ AU to $r \sim 17\,000$ - $55\,000$ AU in nearby star-forming regions (at d = 140- $460\$ pc). Several related studies have been recently carried out at 850 $\mu$ m with SCUBA on JCMT (Chandler & Richer 2000; Hogerheijde & Sandell 2000; Shirley et al. 2000). Our work differs from these studies in that our source sample is larger and much more comprehensive; in particular, it includes all of the known embedded YSOs in a single star-forming cloud, namely Taurus (cf. Sect. 2.1).

The layout of the paper is as follows. In Sect. 2, we present our millimeter continuum mapping survey of the Taurus embedded YSOs, along with several isolated IRAS globules, and some clustered protostars in Perseus. The results and analysis of the density structure of protostellar envelopes are given in Sects. 3 and 4, respectively. Section 5 presents a careful comparison of the protostellar density structure observed in isolated and clustered regions with theoretical predictions of protostellar collapse models. An evolutionary scenario is also given for the Taurus embedded YSOs, believed to be prototypical isolated sources. Our conclusions are summarized in Sect. 6.

2 Millimeter continuum observations

2.1 Source sample and classification

The original goal of our bolometer observations was to make a complete, homogeneous survey for 1.3 mm continuum emission in the embedded YSOs known in the Taurus-Auriga molecular cloud complex (e.g., Myers et al. 1987 - M 87 -; Kenyon et al. 1990 - KHSS90 -; Kenyon & Hartmann 1993; Tamura et al. 1991). Our Taurus subsample thus comprises 26 YSOs which have all been classified as Class I sources, hence candidate protostars (see below), on the basis of their infrared spectral energy distributions (SEDs) (e.g. M 87, KHSS90, and Table 2). It also includes the Class 0 object IRAM 04191+1523 (IRAM 04191 for short) which was discovered in the course of this 1.3 mm continuum survey and is presently undetected shortward of 60 $\mu$ m (see André et al. 1999 - hereafter AMB99).

The Taurus cloud has a relatively low spatial density of YSOs and is believed to be representative of the isolated or distributed mode of low-mass star formation (e.g. Gómez et al. 1993). In this case, it has been argued that stars form as a result of the self-initiated collapse of isolated dense cores, possibly driven by ambipolar diffusion (e.g. Myers 1987; Lizano & Shu 1989; Mouschovias 1991; although see Hartmann 2000). Accordingly, Taurus-Auriga may be the nearest ( $d =140\$ pc) and best example of a major star-forming region where the standard self-similar theory of isolated protostars (see Sect. 1) should apply to a good approximation.

In order to investigate the possible influence of environmental effects on the structure of protostellar envelopes, we then enlarged our initial Taurus sample by including several Bok globules detected by IRAS at d = 160- $460\$ pc (e.g. Benson & Myers 1989; Yun & Clemens 1992), as well as embedded YSOs in the Perseus molecular cloud complex at $d \sim 300\$ pc (e.g. Bachiller et al. 1991a,b). The Bok globules are small isolated molecular clouds, not clearly associated with any star-forming complex (e.g. Clemens & Barvainis 1988; Lee & Myers 1999), that should also resemble the predictions of the standard protostellar model. By contrast, protostellar evolution in cluster-forming clouds such as Perseus and $\rho$ Ophiuchi is likely to depart significantly from scale-free descriptions (e.g. MAN98; see also Sect. 5 below).

Table 1 lists the most common names of each source in the literature (Col. 1), the abbreviated name adopted in this paper (Col. 2), the source 1950 equatorial coordinates (Cols. 3 and 4, based on the reference listed in Col. 8), along with its adopted distance (Col. 5), bolometric temperature (Col. 6), and bolometric luminosity (Col. 7, based on the reference listed in Col. 9). In total, we took 1.3 mm continuum maps toward 49 embedded YSOs, which are broken down into 4 Class II, 30 Class I, and 15 Class 0 sources.

In this classification, Class 0 sources, distinguished by large submillimeter to bolometric luminosity ratios and self-embedded in massive circumstellar envelopes, are believed to be young protostars at the beginning of the main accretion phase (André et al. 1993, 2000 - hereafter AWB93, AWB2000). Class I sources, characterized by rising SEDs from $\sim$ $2~\mu$ m to $\sim$ $25{-}100~\mu$ m, are interpreted as more evolved protostars which have already accumulated the majority of their final stellar mass but are still accreting matter from a residual envelope plus accretion disk (Lada 1987; M87; André & Montmerle 1994 - hereafter AM94; Chen et al. 1995). Class II and Class III YSOs, with falling infrared SEDs, correspond to pre-main sequence (PMS) stars, e.g., T Tauri stars (see Bertout 1989 for a review), surrounded by a circumstellar disk (optically thick and optically thin, respectively). For the practical purposes of this paper, we have assigned an SED class to each source of Table 2 based on the following limiting ranges of bolometric temperature (cf. Chen et al. 1995, 1997; Gregersen et al. 1997): $\mbox{$T_{\mbox{\tiny bol}}$ }< 70\ \mbox{K}$ for Class 0, $70\ \mbox{K}\le \mbox{$T_{\mbox{\tiny bol}}$ }< 650\ \mbox{K}$ for Class I, and $650\ \mbox{K}\le \mbox{$T_{\mbox{\tiny bol}}$ }< 2\,880\$ K for Class II. Note that most of the IRAS Bok globules and Perseus YSOs observed here are confirmed Class 0 protostars (cf. Table 1 of AWB2000).

Table 1: Sample of observed embedded YSOs
IRAS and other Adopted Coordinates d $T_{\mbox{\tiny bol}}$ $L_{\mbox{\tiny bol}}$ Coord. Lum.

source names name ⁽¹⁾ $\alpha_{\rm 1950}$ $\delta_{\rm 1950}$ (pc) (K) ( $L_\odot$ ) ref. ⁽²⁾ ref. ⁽³⁾

M04016+2610 L1489 04 $^{\rm h}$ 01 $^{\rm m}$ 40 $\hbox{$.\!\!^{\rm s}$ }$ 6 26 $\hbox{$^\circ$ }$ 10 $\hbox{$^\prime$ }$ 49 $\hbox{$^{\prime\prime}$ }$ 140 238 3.7 21 22

M04108+2803A M04108-A 04 $^{\rm h}$ 10 $^{\rm m}$ 47 $\hbox{$.\!\!^{\rm s}$ }$ 3 28 $\hbox{$^\circ$ }$ 03 $\hbox{$^\prime$ }$ 49 $\hbox{$^{\prime\prime}$ }$ 140 0.1 21 17

M04108+2803B M04108-B 04 $^{\rm h}$ 10 $^{\rm m}$ 49 $\hbox{$.\!\!^{\rm s}$ }$ 3 28 $\hbox{$^\circ$ }$ 03 $\hbox{$^\prime$ }$ 57 $\hbox{$^{\prime\prime}$ }$ 140 205 0.6 21 17

K04113+2758 K04113 04 $^{\rm h}$ 11 $^{\rm m}$ 20 $\hbox{$.\!\!^{\rm s}$ }$ 8 27 $\hbox{$^\circ$ }$ 58 $\hbox{$^\prime$ }$ 33 $\hbox{$^{\prime\prime}$ }$ 140 606 >1.6 27 17

H04145+2812/V892 Tau Elias1 04 $^{\rm h}$ 15 $^{\rm m}$ 34 $\hbox{$.\!\!^{\rm s}$ }$ 5 28 $\hbox{$^\circ$ }$ 12 $\hbox{$^\prime$ }$ 02 $\hbox{$^{\prime\prime}$ }$ 140 $3\,226$ 16 7 7

K04158+2805 K04158 04 $^{\rm h}$ 15 $^{\rm m}$ 52 $\hbox{$.\!\!^{\rm s}$ }$ 2 28 $\hbox{$^\circ$ }$ 05 $\hbox{$^\prime$ }$ 10 $\hbox{$^{\prime\prime}$ }$ 140 528 >0.4 15 17

K04166+2706 K04166 04 $^{\rm h}$ 16 $^{\rm m}$ 37 $\hbox{$.\!\!^{\rm s}$ }$ 8 27 $\hbox{$^\circ$ }$ 06 $\hbox{$^\prime$ }$ 29 $\hbox{$^{\prime\prime}$ }$ 140 139 0.3 15 17

K04169+2702 K04169 04 $^{\rm h}$ 16 $^{\rm m}$ 53 $\hbox{$.\!\!^{\rm s}$ }$ 8 27 $\hbox{$^\circ$ }$ 02 $\hbox{$^\prime$ }$ 48 $\hbox{$^{\prime\prime}$ }$ 140 170 0.8 15 17

K04181+2655 K04181+2655 04 $^{\rm h}$ 18 $^{\rm m}$ 06 $\hbox{$.\!\!^{\rm s}$ }$ 4 26 $\hbox{$^\circ$ }$ 55 $\hbox{$^\prime$ }$ 01 $\hbox{$^{\prime\prime}$ }$ 140 278 0.4 15 17

K04181+2654 K04181+2654 04 $^{\rm h}$ 18 $^{\rm m}$ 06 $\hbox{$.\!\!^{\rm s}$ }$ 9 26 $\hbox{$^\circ$ }$ 54 $\hbox{$^\prime$ }$ 04 $\hbox{$^{\prime\prime}$ }$ 140 346 0.5 15 17

IRAM04191+1523 IRAM 04191 04 $^{\rm h}$ 19 $^{\rm m}$ 06 $\hbox{$.\!\!^{\rm s}$ }$ 4 15 $\hbox{$^\circ$ }$ 22 $\hbox{$^\prime$ }$ 46 $\hbox{$^{\prime\prime}$ }$ 140 18 0.15 1 1

T04191+1523 T04191 04 $^{\rm h}$ 19 $^{\rm m}$ 09 $\hbox{$.\!\!^{\rm s}$ }$ 6 15 $\hbox{$^\circ$ }$ 23 $\hbox{$^\prime$ }$ 20 $\hbox{$^{\prime\prime}$ }$ 140 210 0.5 27 22

M04239+2436 M04239 04 $^{\rm h}$ 23 $^{\rm m}$ 54 $\hbox{$.\!\!^{\rm s}$ }$ 5 24 $\hbox{$^\circ$ }$ 36 $\hbox{$^\prime$ }$ 54 $\hbox{$^{\prime\prime}$ }$ 140 236 1.3 21 17

M04248+2612/HH31IRS2 M04248 04 $^{\rm h}$ 24 $^{\rm m}$ 52 $\hbox{$.\!\!^{\rm s}$ }$ 7 26 $\hbox{$^\circ$ }$ 12 $\hbox{$^\prime$ }$ 42 $\hbox{$^{\prime\prime}$ }$ 140 334 0.4 21 17

Z04260+2642 Z04260 04 $^{\rm h}$ 26 $^{\rm m}$ 00 $\hbox{$.\!\!^{\rm s}$ }$ 0 26 $\hbox{$^\circ$ }$ 42 $\hbox{$^\prime$ }$ 32 $\hbox{$^{\prime\prime}$ }$ 140 0.1 9 17

04263+2426/GVTauB Haro6-10 04 $^{\rm h}$ 26 $^{\rm m}$ 22 $\hbox{$.\!\!^{\rm s}$ }$ 0 24 $\hbox{$^\circ$ }$ 26 $\hbox{$^\prime$ }$ 30 $\hbox{$^{\prime\prime}$ }$ 140 253 7.0 21 17

K04264+2433 Elias6 04 $^{\rm h}$ 26 $^{\rm m}$ 28 $\hbox{$.\!\!^{\rm s}$ }$ 1 24 $\hbox{$^\circ$ }$ 33 $\hbox{$^\prime$ }$ 24 $\hbox{$^{\prime\prime}$ }$ 140 252 0.5 15 9

F04287+1801 L1551-IRS5 04 $^{\rm h}$ 28 $^{\rm m}$ 40 $\hbox{$.\!\!^{\rm s}$ }$ 2 18 $\hbox{$^\circ$ }$ 01 $\hbox{$^\prime$ }$ 42 $\hbox{$^{\prime\prime}$ }$ 140 97 28 14 10

04287+1806 HH30-IRS 04 $^{\rm h}$ 28 $^{\rm m}$ 43 $\hbox{$.\!\!^{\rm s}$ }$ 3 18 $\hbox{$^\circ$ }$ 06 $\hbox{$^\prime$ }$ 02 $\hbox{$^{\prime\prime}$ }$ 140 > 0.1 20 24

04287+1807/Haro6-14 HLTau 04 $^{\rm h}$ 28 $^{\rm m}$ 44 $\hbox{$.\!\!^{\rm s}$ }$ 4 18 $\hbox{$^\circ$ }$ 07 $\hbox{$^\prime$ }$ 36 $\hbox{$^{\prime\prime}$ }$ 140 576 7.1 7 24

04288+1802 L1551-NE 04 $^{\rm h}$ 28 $^{\rm m}$ 50 $\hbox{$.\!\!^{\rm s}$ }$ 4 18 $\hbox{$^\circ$ }$ 02 $\hbox{$^\prime$ }$ 10 $\hbox{$^{\prime\prime}$ }$ 140 75 6 21 5

M04295+2251/L1536-IRS M04295 04 $^{\rm h}$ 29 $^{\rm m}$ 32 $\hbox{$.\!\!^{\rm s}$ }$ 2 22 $\hbox{$^\circ$ }$ 51 $\hbox{$^\prime$ }$ 11 $\hbox{$^{\prime\prime}$ }$ 140 447 0.6 21 21

04296+1725 GGTau 04 $^{\rm h}$ 29 $^{\rm m}$ 37 $\hbox{$.\!\!^{\rm s}$ }$ 2 17 $\hbox{$^\circ$ }$ 25 $\hbox{$^\prime$ }$ 22 $\hbox{$^{\prime\prime}$ }$ 140 $2\,621$ 2.0 7 17

K04302+2247 K04302 04 $^{\rm h}$ 30 $^{\rm m}$ 16 $\hbox{$.\!\!^{\rm s}$ }$ 8 22 $\hbox{$^\circ$ }$ 47 $\hbox{$^\prime$ }$ 04 $\hbox{$^{\prime\prime}$ }$ 140 202 0.3 16 17

T04325+2402/L1535-IRS T04325 04 $^{\rm h}$ 32 $^{\rm m}$ 33 $\hbox{$.\!\!^{\rm s}$ }$ 5 24 $\hbox{$^\circ$ }$ 02 $\hbox{$^\prime$ }$ 15 $\hbox{$^{\prime\prime}$ }$ 140 157 0.9 27 22

K04361+2547 TMR1 04 $^{\rm h}$ 36 $^{\rm m}$ 09 $\hbox{$.\!\!^{\rm s}$ }$ 8 25 $\hbox{$^\circ$ }$ 47 $\hbox{$^\prime$ }$ 28 $\hbox{$^{\prime\prime}$ }$ 140 144 3.7 16 22

M04365+2535/L1534 TMC1A 04 $^{\rm h}$ 36 $^{\rm m}$ 31 $\hbox{$.\!\!^{\rm s}$ }$ 2 25 $\hbox{$^\circ$ }$ 35 $\hbox{$^\prime$ }$ 56 $\hbox{$^{\prime\prime}$ }$ 140 172 2.4 21 21

K04368+2557 L1527 04 $^{\rm h}$ 36 $^{\rm m}$ 49 $\hbox{$.\!\!^{\rm s}$ }$ 5 25 $\hbox{$^\circ$ }$ 57 $\hbox{$^\prime$ }$ 16 $\hbox{$^{\prime\prime}$ }$ 140 59 1.6 18 15

M04381+2540/TMC1 M04381 04 $^{\rm h}$ 38 $^{\rm m}$ 08 $\hbox{$.\!\!^{\rm s}$ }$ 5 25 $\hbox{$^\circ$ }$ 40 $\hbox{$^\prime$ }$ 53 $\hbox{$^{\prime\prime}$ }$ 140 139 0.7 21 21

M04385+2550/Haro6-33 TMC1C 04 $^{\rm h}$ 38 $^{\rm m}$ 34 $\hbox{$.\!\!^{\rm s}$ }$ 6 25 $\hbox{$^\circ$ }$ 50 $\hbox{$^\prime$ }$ 44 $\hbox{$^{\prime\prime}$ }$ 140 636 >0.4 21 17

M04489+3042 M04489 04 $^{\rm h}$ 48 $^{\rm m}$ 55 $\hbox{$.\!\!^{\rm s}$ }$ 2 30 $\hbox{$^\circ$ }$ 42 $\hbox{$^\prime$ }$ 18 $\hbox{$^{\prime\prime}$ }$ 140 399 0.3 21 21

05417+0907 B35 05 $^{\rm h}$ 41 $^{\rm m}$ 44 $\hbox{$.\!\!^{\rm s}$ }$ 8 09 $\hbox{$^\circ$ }$ 07 $\hbox{$^\prime$ }$ 38 $\hbox{$^{\prime\prime}$ }$ 460 15 28 8

16442-0930 L260 16 $^{\rm h}$ 44 $^{\rm m}$ 13 $\hbox{$.\!\!^{\rm s}$ }$ 9 $-09\hbox{$^\circ$ }$ 29 $\hbox{$^\prime$ }$ 59 $\hbox{$^{\prime\prime}$ }$ 160 1.0 21 21

18148-0440 L483-MM 18 $^{\rm h}$ 14 $^{\rm m}$ 50 $\hbox{$.\!\!^{\rm s}$ }$ 6 $-04\hbox{$^\circ$ }$ 40 $\hbox{$^\prime$ }$ 49 $\hbox{$^{\prime\prime}$ }$ 200 48 14 23 18

18331-0035 L588 18 $^{\rm h}$ 33 $^{\rm m}$ 07 $\hbox{$.\!\!^{\rm s}$ }$ 6 $-00\hbox{$^\circ$ }$ 35 $\hbox{$^\prime$ }$ 48 $\hbox{$^{\prime\prime}$ }$ 200 ? 23

19156+1906 L723-MM 19 $^{\rm h}$ 15 $^{\rm m}$ 42 $\hbox{$.\!\!^{\rm s}$ }$ 0 19 $\hbox{$^\circ$ }$ 06 $\hbox{$^\prime$ }$ 55 $\hbox{$^{\prime\prime}$ }$ 300 39 3 2 12

19345+0727 B335 19 $^{\rm h}$ 34 $^{\rm m}$ 35 $\hbox{$.\!\!^{\rm s}$ }$ 1 07 $\hbox{$^\circ$ }$ 27 $\hbox{$^\prime$ }$ 24 $\hbox{$^{\prime\prime}$ }$ 250 29 3 3 12

20386+6751 L1157-MM 20 $^{\rm h}$ 38 $^{\rm m}$ 39 $\hbox{$.\!\!^{\rm s}$ }$ 6 67 $\hbox{$^\circ$ }$ 51 $\hbox{$^\prime$ }$ 33 $\hbox{$^{\prime\prime}$ }$ 440 42 11 30 30

21106+4712 B361 21 $^{\rm h}$ 10 $^{\rm m}$ 40 $\hbox{$.\!\!^{\rm s}$ }$ 9 47 $\hbox{$^\circ$ }$ 12 $\hbox{$^\prime$ }$ 01 $\hbox{$^{\prime\prime}$ }$ 350 4.7 8 8

23238+7401 L1262 23 $^{\rm h}$ 23 $^{\rm m}$ 48 $\hbox{$.\!\!^{\rm s}$ }$ 7 74 $\hbox{$^\circ$ }$ 01 $\hbox{$^\prime$ }$ 08 $\hbox{$^{\prime\prime}$ }$ 200 2.3 8 29

L1448-NW 03 $^{\rm h}$ 22 $^{\rm m}$ 31 $\hbox{$.\!\!^{\rm s}$ }$ 1 30 $\hbox{$^\circ$ }$ 35 $\hbox{$^\prime$ }$ 04 $\hbox{$^{\prime\prime}$ }$ 300 24 2.7 6 6

03225+3034/L1448-IRS3 L1448-N 03 $^{\rm h}$ 22 $^{\rm m}$ 31 $\hbox{$.\!\!^{\rm s}$ }$ 8 30 $\hbox{$^\circ$ }$ 34 $\hbox{$^\prime$ }$ 45 $\hbox{$^{\prime\prime}$ }$ 300 55 11 11 6

L1448-MM L1448-C 03 $^{\rm h}$ 22 $^{\rm m}$ 34 $\hbox{$.\!\!^{\rm s}$ }$ 3 30 $\hbox{$^\circ$ }$ 33 $\hbox{$^\prime$ }$ 35 $\hbox{$^{\prime\prime}$ }$ 300 55 8 11 6

03258+3104/SVS19 NGC 1333-IRAS 2 03 $^{\rm h}$ 25 $^{\rm m}$ 49 $\hbox{$.\!\!^{\rm s}$ }$ 9 31 $\hbox{$^\circ$ }$ 04 $\hbox{$^\prime$ }$ 16 $\hbox{$^{\prime\prime}$ }$ 350 41 40 26 13

NGC 1333-IRAS 4A 03 $^{\rm h}$ 26 $^{\rm m}$ 04 $\hbox{$.\!\!^{\rm s}$ }$ 8 31 $\hbox{$^\circ$ }$ 03 $\hbox{$^\prime$ }$ 14 $\hbox{$^{\prime\prime}$ }$ 350 34 14 25 25

NGC 1333-IRAS 4B 03 $^{\rm h}$ 26 $^{\rm m}$ 06 $\hbox{$.\!\!^{\rm s}$ }$ 5 31 $\hbox{$^\circ$ }$ 02 $\hbox{$^\prime$ }$ 51 $\hbox{$^{\prime\prime}$ }$ 350 36 14 25 25

03282+3035 IRAS 03282 03 $^{\rm h}$ 28 $^{\rm m}$ 15 $\hbox{$.\!\!^{\rm s}$ }$ 8 30 $\hbox{$^\circ$ }$ 35 $\hbox{$^\prime$ }$ 20 $\hbox{$^{\prime\prime}$ }$ 300 23 1.5 4 6

HH211-MM 03 $^{\rm h}$ 40 $^{\rm m}$ 48 $\hbox{$.\!\!^{\rm s}$ }$ 7 31 $\hbox{$^\circ$ }$ 51 $\hbox{$^\prime$ }$ 24 $\hbox{$^{\prime\prime}$ }$ 300 <10? 19

M03445+3242/B5-B B5-IRS1 03 $^{\rm h}$ 44 $^{\rm m}$ 31 $\hbox{$.\!\!^{\rm s}$ }$ 8 32 $\hbox{$^\circ$ }$ 42 $\hbox{$^\prime$ }$ 34 $\hbox{$^{\prime\prime}$ }$ 300 9.4 21 21

**Table 1:** Sample of observed embedded YSOs
IRAS and other	Adopted	Coordinates	d	$T_{\mbox{\tiny bol}}$	$L_{\mbox{\tiny bol}}$	Coord.	Lum.
source names	name ⁽¹⁾	$\alpha_{\rm 1950}$	$\delta_{\rm 1950}$	(pc)	(K)	( $L_\odot$ )	ref. ⁽²⁾	ref. ⁽³⁾
M04016+2610	L1489	04 $^{\rm h}$ 01 $^{\rm m}$ 40 $\hbox{$.\!\!^{\rm s}$ }$ 6	26 $\hbox{$^\circ$ }$ 10 $\hbox{$^\prime$ }$ 49 $\hbox{$^{\prime\prime}$ }$	140	238	3.7	21	22
M04108+2803A	M04108-A	04 $^{\rm h}$ 10 $^{\rm m}$ 47 $\hbox{$.\!\!^{\rm s}$ }$ 3	28 $\hbox{$^\circ$ }$ 03 $\hbox{$^\prime$ }$ 49 $\hbox{$^{\prime\prime}$ }$	140		0.1	21	17
M04108+2803B	M04108-B	04 $^{\rm h}$ 10 $^{\rm m}$ 49 $\hbox{$.\!\!^{\rm s}$ }$ 3	28 $\hbox{$^\circ$ }$ 03 $\hbox{$^\prime$ }$ 57 $\hbox{$^{\prime\prime}$ }$	140	205	0.6	21	17
K04113+2758	K04113	04 $^{\rm h}$ 11 $^{\rm m}$ 20 $\hbox{$.\!\!^{\rm s}$ }$ 8	27 $\hbox{$^\circ$ }$ 58 $\hbox{$^\prime$ }$ 33 $\hbox{$^{\prime\prime}$ }$	140	606	>1.6	27	17
H04145+2812/V892 Tau	Elias1	04 $^{\rm h}$ 15 $^{\rm m}$ 34 $\hbox{$.\!\!^{\rm s}$ }$ 5	28 $\hbox{$^\circ$ }$ 12 $\hbox{$^\prime$ }$ 02 $\hbox{$^{\prime\prime}$ }$	140	$3\,226$	16	7	7
K04158+2805	K04158	04 $^{\rm h}$ 15 $^{\rm m}$ 52 $\hbox{$.\!\!^{\rm s}$ }$ 2	28 $\hbox{$^\circ$ }$ 05 $\hbox{$^\prime$ }$ 10 $\hbox{$^{\prime\prime}$ }$	140	528	>0.4	15	17
K04166+2706	K04166	04 $^{\rm h}$ 16 $^{\rm m}$ 37 $\hbox{$.\!\!^{\rm s}$ }$ 8	27 $\hbox{$^\circ$ }$ 06 $\hbox{$^\prime$ }$ 29 $\hbox{$^{\prime\prime}$ }$	140	139	0.3	15	17
K04169+2702	K04169	04 $^{\rm h}$ 16 $^{\rm m}$ 53 $\hbox{$.\!\!^{\rm s}$ }$ 8	27 $\hbox{$^\circ$ }$ 02 $\hbox{$^\prime$ }$ 48 $\hbox{$^{\prime\prime}$ }$	140	170	0.8	15	17
K04181+2655	K04181+2655	04 $^{\rm h}$ 18 $^{\rm m}$ 06 $\hbox{$.\!\!^{\rm s}$ }$ 4	26 $\hbox{$^\circ$ }$ 55 $\hbox{$^\prime$ }$ 01 $\hbox{$^{\prime\prime}$ }$	140	278	0.4	15	17
K04181+2654	K04181+2654	04 $^{\rm h}$ 18 $^{\rm m}$ 06 $\hbox{$.\!\!^{\rm s}$ }$ 9	26 $\hbox{$^\circ$ }$ 54 $\hbox{$^\prime$ }$ 04 $\hbox{$^{\prime\prime}$ }$	140	346	0.5	15	17
IRAM04191+1523	IRAM 04191	04 $^{\rm h}$ 19 $^{\rm m}$ 06 $\hbox{$.\!\!^{\rm s}$ }$ 4	15 $\hbox{$^\circ$ }$ 22 $\hbox{$^\prime$ }$ 46 $\hbox{$^{\prime\prime}$ }$	140	18	0.15	1	1
T04191+1523	T04191	04 $^{\rm h}$ 19 $^{\rm m}$ 09 $\hbox{$.\!\!^{\rm s}$ }$ 6	15 $\hbox{$^\circ$ }$ 23 $\hbox{$^\prime$ }$ 20 $\hbox{$^{\prime\prime}$ }$	140	210	0.5	27	22
M04239+2436	M04239	04 $^{\rm h}$ 23 $^{\rm m}$ 54 $\hbox{$.\!\!^{\rm s}$ }$ 5	24 $\hbox{$^\circ$ }$ 36 $\hbox{$^\prime$ }$ 54 $\hbox{$^{\prime\prime}$ }$	140	236	1.3	21	17
M04248+2612/HH31IRS2	M04248	04 $^{\rm h}$ 24 $^{\rm m}$ 52 $\hbox{$.\!\!^{\rm s}$ }$ 7	26 $\hbox{$^\circ$ }$ 12 $\hbox{$^\prime$ }$ 42 $\hbox{$^{\prime\prime}$ }$	140	334	0.4	21	17
Z04260+2642	Z04260	04 $^{\rm h}$ 26 $^{\rm m}$ 00 $\hbox{$.\!\!^{\rm s}$ }$ 0	26 $\hbox{$^\circ$ }$ 42 $\hbox{$^\prime$ }$ 32 $\hbox{$^{\prime\prime}$ }$	140		0.1	9	17
04263+2426/GVTauB	Haro6-10	04 $^{\rm h}$ 26 $^{\rm m}$ 22 $\hbox{$.\!\!^{\rm s}$ }$ 0	24 $\hbox{$^\circ$ }$ 26 $\hbox{$^\prime$ }$ 30 $\hbox{$^{\prime\prime}$ }$	140	253	7.0	21	17
K04264+2433	Elias6	04 $^{\rm h}$ 26 $^{\rm m}$ 28 $\hbox{$.\!\!^{\rm s}$ }$ 1	24 $\hbox{$^\circ$ }$ 33 $\hbox{$^\prime$ }$ 24 $\hbox{$^{\prime\prime}$ }$	140	252	0.5	15	9
F04287+1801	L1551-IRS5	04 $^{\rm h}$ 28 $^{\rm m}$ 40 $\hbox{$.\!\!^{\rm s}$ }$ 2	18 $\hbox{$^\circ$ }$ 01 $\hbox{$^\prime$ }$ 42 $\hbox{$^{\prime\prime}$ }$	140	97	28	14	10
04287+1806	HH30-IRS	04 $^{\rm h}$ 28 $^{\rm m}$ 43 $\hbox{$.\!\!^{\rm s}$ }$ 3	18 $\hbox{$^\circ$ }$ 06 $\hbox{$^\prime$ }$ 02 $\hbox{$^{\prime\prime}$ }$	140		> 0.1	20	24
04287+1807/Haro6-14	HLTau	04 $^{\rm h}$ 28 $^{\rm m}$ 44 $\hbox{$.\!\!^{\rm s}$ }$ 4	18 $\hbox{$^\circ$ }$ 07 $\hbox{$^\prime$ }$ 36 $\hbox{$^{\prime\prime}$ }$	140	576	7.1	7	24
04288+1802	L1551-NE	04 $^{\rm h}$ 28 $^{\rm m}$ 50 $\hbox{$.\!\!^{\rm s}$ }$ 4	18 $\hbox{$^\circ$ }$ 02 $\hbox{$^\prime$ }$ 10 $\hbox{$^{\prime\prime}$ }$	140	75	6	21	5
M04295+2251/L1536-IRS	M04295	04 $^{\rm h}$ 29 $^{\rm m}$ 32 $\hbox{$.\!\!^{\rm s}$ }$ 2	22 $\hbox{$^\circ$ }$ 51 $\hbox{$^\prime$ }$ 11 $\hbox{$^{\prime\prime}$ }$	140	447	0.6	21	21
04296+1725	GGTau	04 $^{\rm h}$ 29 $^{\rm m}$ 37 $\hbox{$.\!\!^{\rm s}$ }$ 2	17 $\hbox{$^\circ$ }$ 25 $\hbox{$^\prime$ }$ 22 $\hbox{$^{\prime\prime}$ }$	140	$2\,621$	2.0	7	17
K04302+2247	K04302	04 $^{\rm h}$ 30 $^{\rm m}$ 16 $\hbox{$.\!\!^{\rm s}$ }$ 8	22 $\hbox{$^\circ$ }$ 47 $\hbox{$^\prime$ }$ 04 $\hbox{$^{\prime\prime}$ }$	140	202	0.3	16	17
T04325+2402/L1535-IRS	T04325	04 $^{\rm h}$ 32 $^{\rm m}$ 33 $\hbox{$.\!\!^{\rm s}$ }$ 5	24 $\hbox{$^\circ$ }$ 02 $\hbox{$^\prime$ }$ 15 $\hbox{$^{\prime\prime}$ }$	140	157	0.9	27	22
K04361+2547	TMR1	04 $^{\rm h}$ 36 $^{\rm m}$ 09 $\hbox{$.\!\!^{\rm s}$ }$ 8	25 $\hbox{$^\circ$ }$ 47 $\hbox{$^\prime$ }$ 28 $\hbox{$^{\prime\prime}$ }$	140	144	3.7	16	22
M04365+2535/L1534	TMC1A	04 $^{\rm h}$ 36 $^{\rm m}$ 31 $\hbox{$.\!\!^{\rm s}$ }$ 2	25 $\hbox{$^\circ$ }$ 35 $\hbox{$^\prime$ }$ 56 $\hbox{$^{\prime\prime}$ }$	140	172	2.4	21	21
K04368+2557	L1527	04 $^{\rm h}$ 36 $^{\rm m}$ 49 $\hbox{$.\!\!^{\rm s}$ }$ 5	25 $\hbox{$^\circ$ }$ 57 $\hbox{$^\prime$ }$ 16 $\hbox{$^{\prime\prime}$ }$	140	59	1.6	18	15
M04381+2540/TMC1	M04381	04 $^{\rm h}$ 38 $^{\rm m}$ 08 $\hbox{$.\!\!^{\rm s}$ }$ 5	25 $\hbox{$^\circ$ }$ 40 $\hbox{$^\prime$ }$ 53 $\hbox{$^{\prime\prime}$ }$	140	139	0.7	21	21
M04385+2550/Haro6-33	TMC1C	04 $^{\rm h}$ 38 $^{\rm m}$ 34 $\hbox{$.\!\!^{\rm s}$ }$ 6	25 $\hbox{$^\circ$ }$ 50 $\hbox{$^\prime$ }$ 44 $\hbox{$^{\prime\prime}$ }$	140	636	>0.4	21	17
M04489+3042	M04489	04 $^{\rm h}$ 48 $^{\rm m}$ 55 $\hbox{$.\!\!^{\rm s}$ }$ 2	30 $\hbox{$^\circ$ }$ 42 $\hbox{$^\prime$ }$ 18 $\hbox{$^{\prime\prime}$ }$	140	399	0.3	21	21
05417+0907	B35	05 $^{\rm h}$ 41 $^{\rm m}$ 44 $\hbox{$.\!\!^{\rm s}$ }$ 8	09 $\hbox{$^\circ$ }$ 07 $\hbox{$^\prime$ }$ 38 $\hbox{$^{\prime\prime}$ }$	460		15	28	8
16442-0930	L260	16 $^{\rm h}$ 44 $^{\rm m}$ 13 $\hbox{$.\!\!^{\rm s}$ }$ 9	$-09\hbox{$^\circ$ }$ 29 $\hbox{$^\prime$ }$ 59 $\hbox{$^{\prime\prime}$ }$	160		1.0	21	21
18148-0440	L483-MM	18 $^{\rm h}$ 14 $^{\rm m}$ 50 $\hbox{$.\!\!^{\rm s}$ }$ 6	$-04\hbox{$^\circ$ }$ 40 $\hbox{$^\prime$ }$ 49 $\hbox{$^{\prime\prime}$ }$	200	48	14	23	18
18331-0035	L588	18 $^{\rm h}$ 33 $^{\rm m}$ 07 $\hbox{$.\!\!^{\rm s}$ }$ 6	$-00\hbox{$^\circ$ }$ 35 $\hbox{$^\prime$ }$ 48 $\hbox{$^{\prime\prime}$ }$	200		?	23
19156+1906	L723-MM	19 $^{\rm h}$ 15 $^{\rm m}$ 42 $\hbox{$.\!\!^{\rm s}$ }$ 0	19 $\hbox{$^\circ$ }$ 06 $\hbox{$^\prime$ }$ 55 $\hbox{$^{\prime\prime}$ }$	300	39	3	2	12
19345+0727	B335	19 $^{\rm h}$ 34 $^{\rm m}$ 35 $\hbox{$.\!\!^{\rm s}$ }$ 1	07 $\hbox{$^\circ$ }$ 27 $\hbox{$^\prime$ }$ 24 $\hbox{$^{\prime\prime}$ }$	250	29	3	3	12
20386+6751	L1157-MM	20 $^{\rm h}$ 38 $^{\rm m}$ 39 $\hbox{$.\!\!^{\rm s}$ }$ 6	67 $\hbox{$^\circ$ }$ 51 $\hbox{$^\prime$ }$ 33 $\hbox{$^{\prime\prime}$ }$	440	42	11	30	30
21106+4712	B361	21 $^{\rm h}$ 10 $^{\rm m}$ 40 $\hbox{$.\!\!^{\rm s}$ }$ 9	47 $\hbox{$^\circ$ }$ 12 $\hbox{$^\prime$ }$ 01 $\hbox{$^{\prime\prime}$ }$	350		4.7	8	8
23238+7401	L1262	23 $^{\rm h}$ 23 $^{\rm m}$ 48 $\hbox{$.\!\!^{\rm s}$ }$ 7	74 $\hbox{$^\circ$ }$ 01 $\hbox{$^\prime$ }$ 08 $\hbox{$^{\prime\prime}$ }$	200		2.3	8	29
	L1448-NW	03 $^{\rm h}$ 22 $^{\rm m}$ 31 $\hbox{$.\!\!^{\rm s}$ }$ 1	30 $\hbox{$^\circ$ }$ 35 $\hbox{$^\prime$ }$ 04 $\hbox{$^{\prime\prime}$ }$	300	24	2.7	6	6
03225+3034/L1448-IRS3	L1448-N	03 $^{\rm h}$ 22 $^{\rm m}$ 31 $\hbox{$.\!\!^{\rm s}$ }$ 8	30 $\hbox{$^\circ$ }$ 34 $\hbox{$^\prime$ }$ 45 $\hbox{$^{\prime\prime}$ }$	300	55	11	11	6
L1448-MM	L1448-C	03 $^{\rm h}$ 22 $^{\rm m}$ 34 $\hbox{$.\!\!^{\rm s}$ }$ 3	30 $\hbox{$^\circ$ }$ 33 $\hbox{$^\prime$ }$ 35 $\hbox{$^{\prime\prime}$ }$	300	55	8	11	6
03258+3104/SVS19	NGC 1333-IRAS 2	03 $^{\rm h}$ 25 $^{\rm m}$ 49 $\hbox{$.\!\!^{\rm s}$ }$ 9	31 $\hbox{$^\circ$ }$ 04 $\hbox{$^\prime$ }$ 16 $\hbox{$^{\prime\prime}$ }$	350	41	40	26	13
	NGC 1333-IRAS 4A	03 $^{\rm h}$ 26 $^{\rm m}$ 04 $\hbox{$.\!\!^{\rm s}$ }$ 8	31 $\hbox{$^\circ$ }$ 03 $\hbox{$^\prime$ }$ 14 $\hbox{$^{\prime\prime}$ }$	350	34	14	25	25
	NGC 1333-IRAS 4B	03 $^{\rm h}$ 26 $^{\rm m}$ 06 $\hbox{$.\!\!^{\rm s}$ }$ 5	31 $\hbox{$^\circ$ }$ 02 $\hbox{$^\prime$ }$ 51 $\hbox{$^{\prime\prime}$ }$	350	36	14	25	25
03282+3035	IRAS 03282	03 $^{\rm h}$ 28 $^{\rm m}$ 15 $\hbox{$.\!\!^{\rm s}$ }$ 8	30 $\hbox{$^\circ$ }$ 35 $\hbox{$^\prime$ }$ 20 $\hbox{$^{\prime\prime}$ }$	300	23	1.5	4	6
	HH211-MM	03 $^{\rm h}$ 40 $^{\rm m}$ 48 $\hbox{$.\!\!^{\rm s}$ }$ 7	31 $\hbox{$^\circ$ }$ 51 $\hbox{$^\prime$ }$ 24 $\hbox{$^{\prime\prime}$ }$	300		<10?	19
M03445+3242/B5-B	B5-IRS1	03 $^{\rm h}$ 44 $^{\rm m}$ 31 $\hbox{$.\!\!^{\rm s}$ }$ 8	32 $\hbox{$^\circ$ }$ 42 $\hbox{$^\prime$ }$ 34 $\hbox{$^{\prime\prime}$ }$	300		9.4	21	21

Notes: ⁽¹⁾ The first letter of the adopted name generally refers to source samples. Thus, "L'' corresponds to the Lynds catalogue (1962); "M'' and "K'' recall IRAS sources selected by M 87 and Kenyon et al. (1990, 1993a, 1993); "H'' and "T'' indicate sources studied by Heyer et al. (1987) and Tamura et al. (1991); "Z'' and "F'' refer to Beichman et al. (1986). ⁽²⁾ and ⁽³⁾ References: (1) AMB99; (2) and (3) Anglada et al. (1991, 1992); (4) Bachiller et al. (1994); (5) and (6) Barsony et al. (1993, 1998); (7) Beckwith et al. (1990); (8) and (9) Beichman et al. (1986, 1992); (10) Butner et al. (1991); (11) Curiel et al. (1990); (12) Davidson (1987); (13) Jennings et al. (1987); (14) Keene & Masson (1990); (15) KHSS90; (16) KCH93; (17) Kenyon & Hartmann (1993); (18) Ladd et al. (1991); (19) McCaughrean et al. (1994); (20) Mundt et al. (1987); (21) M 87; (22) Ohashi et al. (1996); (23) Parker (1988); (24) Reipurth et al. (1993); (25) and (26) Sandell et al. (1991, 1994); (27) Tamura et al. (1991); (28) and (29) Terebey et al. (1992, 1993); (30) Umemoto et al. (1992).

2.2 Bolometer mapping

We carried out our 1.3 mm mapping survey during five observing sessions from 1993 to 1999. All the runs were performed using the IRAM 30 m telescope on Pico Veleta (Spain) and the MPIfR bolometer arrays (now called MAMBO, e.g. Kreysa et al. 1998) with 7 channels (in 1993 and 1994), 19 channels (in 1995 and 1996), and 37 channels (in 1999). The passband of these bolometers has an equivalent width $\approx$ 70 GHz and is centered at $\nu_{\rm eff} \approx 240$ GHz (e.g. Kreysa et al. 1998).

Each YSO of Table 1 was first observed at its nominal infrared position in the "on-off'' observing mode, and then mapped in the "multi-point'' or "on-the-fly'' mode.

The multi-point mapping mode was mainly used in 1993, for sources which were too weak to be observed in the on-the-fly mapping mode with the 7-channel bolometer. Each multi-point map consists of several (>5) on-off integrations giving fluxes at a few ( $> 5 \times 7 = 35$ ) offsets around the nominal source position.

In the dual-beam on-the-fly mapping mode, the telescope is scanned continuously in azimuth along each row while wobbling. For each channel, the raw data corresponding to a single on-the-fly coverage consist of several rows taken at a series of elevations. We used a scanning velocity of 4 $\hbox{$^{\prime\prime}$ }$ /s or 8 $\hbox{$^{\prime\prime}$ }$ /s, and a sampling of 2 $\hbox{$^{\prime\prime}$ }$ (resp. 4 $\hbox{$^{\prime\prime}$ }$ ) in azimuth and 4 $\hbox{$^{\prime\prime}$ }$ in elevation. The wobbler frequency was set to 2 Hz and the wobbler throw (in azimuth) was typically 32 $\hbox{$^{\prime\prime}$ }$ . The typical size of the maps depends on the bolometer array used: $\sim$ $1\hbox{$^\prime$ }\times 1\hbox{$^\prime$ }$ , $\sim$ $3\hbox{$^\prime$ }\times 2\hbox{$^\prime$ }$ , and $\sim$ $4\hbox{$^\prime$ }\times 3\hbox{$^\prime$ }$ for the 7-channel, 19-channel, and 37-channel arrays, respectively.

The dual-beam maps were reduced with the IRAM software for bolometer-array data ("NIC''; cf. Broguière et al. 1995) which uses the EKH restoration algorithm (Emerson et al. 1979).

The FWHM size of the main beam was measured to be $HPBW \sim 11\hbox{$^{\prime\prime}$ }-12\hbox{$^{\prime\prime}$ }$ using Uranus, Mars, and other strong point-like sources such as quasars. The absolute pointing of the telescope was checked every $\sim$ 1 hr and found to be accurate to better than $\sim$ $3\hbox{$^{\prime\prime}$ }$ - $5\hbox{$^{\prime\prime}$ }$ (maximum deviation in both coordinates).

Most of the data benefited from good weather conditions. The zenith atmospheric optical depth, monitored by "skydips'' every 1-2 hr, was between $\sim$ 0.1 and $\sim$ 0.4. Calibration was achieved through on-the-fly mapping and on-off observations of the primary calibrators Uranus and Mars (e.g. Griffin & Orton 1993 and references therein). In addition, L1551-IRS5 and L1448-N were used as secondary calibrators in Taurus and Perseus, respectively. The 1.3 mm flux densities adopted for L1551-IRS5 are $\sim$ 1.5 Jy in an $11\hbox{$^{\prime\prime}$ }$ beam and $\sim$ 3.4 Jy integrated over a $60\hbox{$^{\prime\prime}$ }$ diameter aperture. L1551-IRS5 was mapped once a day and observed in the on-off mode before and after each YSO map in Taurus. Likewise, L1448-N whose adopted 1.3 mm peak flux is $\sim$ 4.1 Jy/beam was observed before and after each map in Perseus. The relative calibration accuracy was found to be better than $\sim$ 10% in Taurus by comparing independent observations of sources mapped several times. Within the subsample of isolated IRAS globules and Perseus protostars, the relative calibration accuracy is slightly worse, i.e., $\sim$ 20%. The overall, absolute calibration uncertainty is estimated to be $\sim$ 20%.

3 Results: 1.3 mm continuum images
and circumstellar masses

Our on-the-fly 1.3 mm continuum maps are presented in Figs. 1 and 9 (for Taurus sources), in Figs. 2a-c and 10a-d (for isolated globules), and in Figs. 2d,e and 10e-g (for YSOs in Perseus). (Figs. 9 and 10 are only available in electronic form at http://www.edpsciences.org.)

It is apparent from the maps that most sources are associated with spatially resolved 1.3 mm dust emission, as expected for "bona fide'' embedded protostars surrounded by extended, relatively massive circumstellar envelopes. Surprisingly enough, however, 10 of the 27 candidate protostars of our Taurus subsample are barely resolved and one (K04181+2655) is even not detected. In the following, these 11 Taurus embedded YSOs, as well as the isolated IRAS globule L260 (with similar 1.3 mm properties), will be called "peculiar Class I sources''.

The maps also demonstrate that none of the objects of our sample is truly isolated. Most, if not all, of them must have formed in groups (especially in Perseus). At least seven of our maps show evidence for diffuse cloud emission and reveal the presence of new starless dense cores/fragments in the vicinity of the targeted YSOs of Table 1 (see Col. 8 of Table 2).

Basic information extracted from these maps is provided in Table 2 for the YSO sources of Table 1, and in Table 3 for the dense cores without IRAS emission. Table 2 lists the adopted name (Col. 1), the SED class (Col. 2, determined from the $\mbox{$T_{\mbox{\tiny bol}}$ }$ value of Table 1), the observing mode and year of observation (Col. 3), the peak and integrated flux densities (Cols. 4 and 5), the estimated circumstellar mass within a radius of $4\,200$ AU (Col. 6), the degree of flux concentration ( $\mbox{$S^{\mbox{\tiny 11\hbox{$^{\prime\prime}$ }}}/S^{\mbox{\tiny 60\hbox{$^{\prime\prime}$ }}}$ }$ in Col. 7), and a short description of the source environment (Col. 8). Table 3 gives similar information for the new starless cores.

Table 2: Circumstellar fluxes and masses
Adopted SED Observing $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~peak}}$ ⁽²⁾ $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ ⁽³⁾ $M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ ⁽⁴⁾ Concentration Source

source name class method ⁽¹⁾ (mJy/beam) (mJy) ( $M_\odot$ ) $S^{\mbox{\tiny 11\hbox{$^{\prime\prime}$ }}}/S^{\mbox{\tiny 60\hbox{$^{\prime\prime}$ }}}$ ⁽⁵⁾ environment

L1489 I 6 $\times$ otf9699 $130\pm5$ 150 0.03 U, 90% L1489-NH3

M04108-A II 2 $\times$ otf99 < 20 - < 0.002 - L1495N-NH3

M04108-B I 2 $\times$ otf99 $39 \pm5$ 39 0.008 U, 100% L1495N-NH3

K04113 I otf99 $410\pm40$ 750 0.4 55% diffuse cloud

Elias1 II otf94 $270\pm35$ 270 0.03 U, 100%

K04158 I otf96 $110\pm5$ 110 0.025 U, 100%

K04166 0/I 2 $\times$ otf9599 $180\pm8$ 800 0.45 20%

K04169 I 2 $\times$ otf9599 $190\pm9$ 730 0.40 30% K04169-NW

K04181+2655 I 2 $\times$ otf9699 < 10 - < 0.002 - K04181+2654

K04181+2654 I 2 $\times$ otf9699 $50\pm8$ 230 0.12 20%

IRAM04191 0 3 $\times$ otf9599 $110\pm7$ 650 0.45 $^{\mbox{\tiny 12.5K}}$ 20% T04191

T04191 I 3 $\times$ otf9599 $110\pm7$ 400 0.2 30% IRAM04191

M04239 I mpt93 $80\pm10$ 170 $\sim$ 0.09 $\sim50\%$

M04248 I 2 $\times$ otf99 $60\pm7$ 450 0.25 10% B217-NH3

Z04260 I 2 $\times$ otf99 $105\pm10$ 120 0.025 U, 90%

Haro6-10 I 2 $\times$ mpt93 $100\pm10$ 200 $\sim$ $0.07^{\mbox{\tiny 20K}}$ $\sim$ 50%

Elias6 I otf99 $31\pm8$ 31 0.007 U, 100%

L1551-IRS5 I 4 $\times$ otf99 $1\,500\pm7$ $3\,400$ 0.90 $^{\mbox{\tiny 25K}}$ 40% L1551-NE

HH30-IRS I/II otf99 $35\pm10$ 35 0.008 U, 100% HLTau, diffuse cloud

HLTau II otf99 $960\pm10$ $1\,200$ 0.13 U, 80% diffuse cloud

L1551-NE I 2 $\times$ otf99 $850\pm10$ $1\,500$ 0.55 $^{\mbox{\tiny 20K}}$ 60% IRS5, cloud fragments

M04295 I otf96 $115\pm10$ 115 0.025 U, 100%

GGTau II otf93 $665\pm10$ 665 0.07 U, 100%

K04302 I otf96 $180\pm10$ 180 0.04 U, 100%

T04325 I 3 $\times$ otf99 $110\pm7$ 520 0.3 20% L1535-NW, cl. fragment

TMR1 I otf99 $110\pm8$ 440 0.25 25% diffuse cloud

TMC1A I mpt93 $230\pm10$ 450 $\sim$ 0.25 $\sim$ 50%

L1527 0 2 $\times$ otf95 $375\pm6$ $1\,500$ 0.80 25% cloud fragment

M04381 I otf99 $70\pm9$ 300 0.16 20% diffuse cloud

TMC1C I otf99 $30\pm5$ 30 0.007 U, 100%

M04489 I otf99 $15\pm4$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }15$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }0.003$ U, 100%

B35 I mpt93 $210\pm5$ 820 $\sim$ 4.0 $\sim$ 30%

L260 I otf94 $110\pm5$ 110 0.03 U, 100% diffuse cloud L260-NH3

L483-MM 0 otf93 $290\pm15$ $1\,100$ 0.8 15%

L588 I otf93 $295\pm5$ 570 0.4 40%

L723-MM 0 otf94 $270\pm 20$ 370 0.6 40%

B335 0 3 $\times$ otf9495 $270\pm 5$ 780 0.9 20%

L1157-MM 0 otf94 $630\pm10$ 630 2.0 40%

B361 I otf96 $170\pm10$ 190 0.4 50% B361-NH3

L1262 I 2 $\times$ mpt94 $120\pm 15$ 500 $\sim$ 0.35 $\sim$ 20%

L1448-NW 0 otf93 $560\pm25$ 900 1.5 35% L1448-N and cloud

L1448-N 0 otf93 $1\,400\pm5$ $2\,100$ 3.5 40% L1448-C, -NW and cloud

L1448-C 0 otf93 $620\pm15$ 910 1.5 40% L1448-N and cloud

NGC 1333-IRAS 2 0 otf94 $830\pm12$ 875 1.2 $^{\mbox{\tiny 30K}}$ 40% cloud fragment

NGC 1333-IRAS 4A 0 otf93 $4\,100\pm20$ $4\,100$ 4.5 $^{\mbox{\tiny 35K}}$ 65% IRAS 4B and cloud

NGC 1333-IRAS 4B 0 otf93 $1\,470\pm40$ $1\,500$ 1.7 $^{\mbox{\tiny 35K}}$ U, 90% IRAS 4A

IRAS 03282 0 otf95 $415\pm10$ 590 1.4 $^{\mbox{\tiny 15K}}$ 40%

HH211-MM 0 otf95 $395\pm15$ 900 1.5 30% cloud fragment

B5-IRS1 I mpt93 $80\pm5$ 200 $\sim$ 0.35 $\sim$ 40%

**Table 2:** Circumstellar fluxes and masses
Adopted	SED	Observing	$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~peak}}$ ⁽²⁾	$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ ⁽³⁾	$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ ⁽⁴⁾	Concentration	Source
source name	class	method ⁽¹⁾	(mJy/beam)	(mJy)	( $M_\odot$ )	$S^{\mbox{\tiny 11\hbox{$^{\prime\prime}$ }}}/S^{\mbox{\tiny 60\hbox{$^{\prime\prime}$ }}}$ ⁽⁵⁾	environment
L1489	I	6 $\times$ otf9699	$130\pm5$	150	0.03	U, 90%	L1489-NH3
M04108-A	II	2 $\times$ otf99	< 20	-	< 0.002	-	L1495N-NH3
M04108-B	I	2 $\times$ otf99	$39 \pm5$	39	0.008	U, 100%	L1495N-NH3
K04113	I	otf99	$410\pm40$	750	0.4	55%	diffuse cloud
Elias1	II	otf94	$270\pm35$	270	0.03	U, 100%
K04158	I	otf96	$110\pm5$	110	0.025	U, 100%
K04166	0/I	2 $\times$ otf9599	$180\pm8$	800	0.45	20%
K04169	I	2 $\times$ otf9599	$190\pm9$	730	0.40	30%	K04169-NW
K04181+2655	I	2 $\times$ otf9699	< 10	-	< 0.002	-	K04181+2654
K04181+2654	I	2 $\times$ otf9699	$50\pm8$	230	0.12	20%
IRAM04191	0	3 $\times$ otf9599	$110\pm7$	650	0.45 $^{\mbox{\tiny 12.5K}}$	20%	T04191
T04191	I	3 $\times$ otf9599	$110\pm7$	400	0.2	30%	IRAM04191
M04239	I	mpt93	$80\pm10$	170	$\sim$ 0.09	$\sim50\%$
M04248	I	2 $\times$ otf99	$60\pm7$	450	0.25	10%	B217-NH3
Z04260	I	2 $\times$ otf99	$105\pm10$	120	0.025	U, 90%
Haro6-10	I	2 $\times$ mpt93	$100\pm10$	200	$\sim$ $0.07^{\mbox{\tiny 20K}}$	$\sim$ 50%
Elias6	I	otf99	$31\pm8$	31	0.007	U, 100%
L1551-IRS5	I	4 $\times$ otf99	$1\,500\pm7$	$3\,400$	0.90 $^{\mbox{\tiny 25K}}$	40%	L1551-NE
HH30-IRS	I/II	otf99	$35\pm10$	35	0.008	U, 100%	HLTau, diffuse cloud
HLTau	II	otf99	$960\pm10$	$1\,200$	0.13	U, 80%	diffuse cloud
L1551-NE	I	2 $\times$ otf99	$850\pm10$	$1\,500$	0.55 $^{\mbox{\tiny 20K}}$	60%	IRS5, cloud fragments
M04295	I	otf96	$115\pm10$	115	0.025	U, 100%
GGTau	II	otf93	$665\pm10$	665	0.07	U, 100%
K04302	I	otf96	$180\pm10$	180	0.04	U, 100%
T04325	I	3 $\times$ otf99	$110\pm7$	520	0.3	20%	L1535-NW, cl. fragment
TMR1	I	otf99	$110\pm8$	440	0.25	25%	diffuse cloud
TMC1A	I	mpt93	$230\pm10$	450	$\sim$ 0.25	$\sim$ 50%
L1527	0	2 $\times$ otf95	$375\pm6$	$1\,500$	0.80	25%	cloud fragment
M04381	I	otf99	$70\pm9$	300	0.16	20%	diffuse cloud
TMC1C	I	otf99	$30\pm5$	30	0.007	U, 100%
M04489	I	otf99	$15\pm4$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }15$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }0.003$	U, 100%
B35	I	mpt93	$210\pm5$	820	$\sim$ 4.0	$\sim$ 30%
L260	I	otf94	$110\pm5$	110	0.03	U, 100%	diffuse cloud L260-NH3
L483-MM	0	otf93	$290\pm15$	$1\,100$	0.8	15%
L588	I	otf93	$295\pm5$	570	0.4	40%
L723-MM	0	otf94	$270\pm 20$	370	0.6	40%
B335	0	3 $\times$ otf9495	$270\pm 5$	780	0.9	20%
L1157-MM	0	otf94	$630\pm10$	630	2.0	40%
B361	I	otf96	$170\pm10$	190	0.4	50%	B361-NH3
L1262	I	2 $\times$ mpt94	$120\pm 15$	500	$\sim$ 0.35	$\sim$ 20%
L1448-NW	0	otf93	$560\pm25$	900	1.5	35%	L1448-N and cloud
L1448-N	0	otf93	$1\,400\pm5$	$2\,100$	3.5	40%	L1448-C, -NW and cloud
L1448-C	0	otf93	$620\pm15$	910	1.5	40%	L1448-N and cloud
NGC 1333-IRAS 2	0	otf94	$830\pm12$	875	1.2 $^{\mbox{\tiny 30K}}$	40%	cloud fragment
NGC 1333-IRAS 4A	0	otf93	$4\,100\pm20$	$4\,100$	4.5 $^{\mbox{\tiny 35K}}$	65%	IRAS 4B and cloud
NGC 1333-IRAS 4B	0	otf93	$1\,470\pm40$	$1\,500$	1.7 $^{\mbox{\tiny 35K}}$	U, 90%	IRAS 4A
IRAS 03282	0	otf95	$415\pm10$	590	1.4 $^{\mbox{\tiny 15K}}$	40%
HH211-MM	0	otf95	$395\pm15$	900	1.5	30%	cloud fragment
B5-IRS1	I	mpt93	$80\pm5$	200	$\sim$ 0.35	$\sim$ 40%

Notes: (1) Number, method and date of 1.3 mm observations: "otf'' = on-the-fly map; "mpt'' = multi-point map. (2) Peak flux in a 11 $\hbox{$^{\prime\prime}$ }$ -12 $\hbox{$^{\prime\prime}$ }$ beam at source peak. Uncertainty corresponds to $1\sigma$ noise level of on-off and map measurements at peak position, upper limits are $3\sigma$ . (3) Flux integrated over a $4\,200$ AU radius circle for on-the-fly maps, Gaussian integrated flux for multi-point maps. (4) Circumstellar mass within a $4\,200$ AU radius circle: approximate value derived from multi-point maps. Assumptions on dust opacity and dust temperature are given in Sect. 3.1. (5) Ratio of peak flux (in 11 $\hbox{$^{\prime\prime}$ }$ -beam) to integrated flux in 60 $\hbox{$^{\prime\prime}$ }$ diameter circle. "U'' indicates unresolved sources.

$\begin{figure} \par\includegraphics[angle=270,width=18cm,clip]{ms10015f1ab.eps}\par\includegraphics[angle=270,width=18cm,clip]{ms10015f1cd.eps}\end{figure}$

Figure 1: Selection of on-the-fly 1.3 mm continuum maps obtained toward Taurus embedded YSOs (all smoothed to a $13\hbox {$^{\prime \prime }$ }$ effective beam). The positions of YSOs with weak emission and starless fragments are marked by stars and crosses, respectively. Contour levels and rms noise at map center are: a) 15 to 120 by 15 mJy/beam, $1\sigma \simeq 4$ mJy/beam; b) 35, 70, 105 mJy/beam, $1\sigma \simeq 9.5$ mJy/beam; c) 90 to 450 by 90 mJy/beam, $1\sigma \simeq 27$ mJy/beam; d) 25 to 200 by 25 mJy/beam, $1\sigma \simeq 6\$ to 7 mJy/beam

$\begin{figure} \par\includegraphics[angle=270,width=18cm,clip]{ms10015f1ef.eps}\... ...ps}\par\includegraphics[angle=270,width=18cm,clip]{ms10015f1ij.eps} \end{figure}$

Figure 1: continued. Contour levels and rms noise at map center are: e) 17 to 136 by 17 mJy/beam, $1\sigma \simeq 5$ mJy/beam; f) 17 to 68 by 17 mJy/beam, $1\sigma \simeq 5$ mJy/beam; g) 25 to 150 by 25 mJy/beam, then 200 to 800 by 200 mJy/beam and 1.2, 1.6 Jy/beam, $1\sigma \simeq 6\$ to 9 mJy/beam; h) 40 to 200 by 40 mJy/beam and then 300, 600, 900 mJy/beam, $1\sigma \simeq 12$ mJy/beam; i) 17 to 187 by 17 mJy/beam, $1\sigma \simeq 5$ mJy/beam; j) 15 to 135 by 15 mJy/beam, $1\sigma \simeq 4.5$ mJy/beam

$\begin{figure} \par\includegraphics[angle=270,width=18cm,clip]{ms10015f1klm.eps} \end{figure}$

Figure 1: continued. Contour levels and rms noise at map center are: k) 40, 80, 120 mJy/beam, $1\sigma \simeq 11$ mJy/beam; l) 12 to 120 by 12 mJy/beam and 180 to 420 by 60 mJy/beam, $1\sigma \simeq 3.5$ mJy/beam; m) 25, 50, 75 mJy/beam, $1\sigma \simeq 7$ mJy/beam. The outflow axis and proposed companion of L1527 are marked with arrows and a filled square marker in l) (cf. MacLeod et al. 1994; Fuller et al. 1996, respectively). See complementary Fig. 9 within the on-line version of this paper

$\begin{figure} \par\includegraphics[angle=270,width=18cm,clip]{ms10015f2abc.eps}\par\includegraphics[angle=270,width=18cm,clip]{ms10015f2de.eps}\end{figure}$

Figure 2: Same as Fig. 1 for several isolated IRAS globules ( a- c) and Perseus protostars ( d, e). Contour levels and rms noise at map center are: a) 12 to 96 by 12 mJy/beam and 150 to 300 by 50 mJy/beam, $1\sigma \simeq 3.5$ mJy/beam; b) 25 to 175 by 25 mJy/beam, $1\sigma \simeq 7.5$ mJy/beam; c) 40 to 120 by 40 mJy/beam and 200 to 600 by 80 mJy/beam, $1\sigma \simeq 11$ mJy/beam; d) 25 to 100 by 25 mJy/beam and 150 to 450 by 50 mJy/beam, $1\sigma \simeq 7.5$ mJy/beam; e) 30, 60, 90 mJy/beam and 150 to 500 by 50 mJy/beam, $1\sigma \simeq 8.5$ mJy/beam. The axis of the B335 outflow is indicated by arrows in a). See complementary Fig. 10 on-line

Table 3: Cold dense cores with no IRAS emission
Core Coordinates d $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~peak}}$ ⁽²⁾ $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ ⁽³⁾ $M^{\mbox{\tiny 4200~AU}}$ ⁽⁴⁾ $R_{\mbox{\tiny out}}$ ⁽⁵⁾ $M^{\mbox{\tiny\mbox{$R_{\mbox{\tiny out}}$ }}}$ ⁽⁶⁾

name ⁽¹⁾ $\alpha_{\rm 1950}$ $\delta_{\rm 1950}$ (pc) (mJy/beam) (mJy) ( $M_\odot$ ) (AU) ( $M_\odot$ )

L1489-NH3 04 $^{\rm h}$ 01 $^{\rm m}$ 45 $\hbox{$.\!\!^{\rm s}$ }$ 7 26 $\hbox{$^\circ$ }$ 11 $\hbox{$^\prime$ }$ 10 $\hbox{$^{\prime\prime}$ }$ 140 $55\pm5$ 510 1.0 $15\,000\pm 3\,000$ 4.

L1495N-NH3 04 $^{\rm h}$ 10 $^{\rm m}$ 45 $\hbox{$.\!\!^{\rm s}$ }$ 0^* 28 $\hbox{$^\circ$ }$ 05 $\hbox{$^\prime$ }$ 40 $\hbox{$^{\prime\prime}$ }$ ^* 140 $(45\pm15)$ ^* $\sim$ 500 $\sim$ 1.0 $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }14\,000$ >5.0^*

K04169-NW 04 $^{\rm h}$ 16 $^{\rm m}$ 47 $\hbox{$.\!\!^{\rm s}$ }$ 4 27 $\hbox{$^\circ$ }$ 04 $\hbox{$^\prime$ }$ 05 $\hbox{$^{\prime\prime}$ }$ 140 $50\pm15$ 340 0.7 $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }14\,000$ 2.5

B217-NH3 04 $^{\rm h}$ 24 $^{\rm m}$ 45 $\hbox{$.\!\!^{\rm s}$ }$ 8 26 $\hbox{$^\circ$ }$ 11 $\hbox{$^\prime$ }$ 30 $\hbox{$^{\prime\prime}$ }$ 140 $55\pm10$ 560 1.1 $14\,000\pm 1\,500$ 5.5

L1535-NE 04 $^{\rm h}$ 32 $^{\rm m}$ 36 $\hbox{$.\!\!^{\rm s}$ }$ 3 24 $\hbox{$^\circ$ }$ 03 $\hbox{$^\prime$ }$ 14 $\hbox{$^{\prime\prime}$ }$ 140 $100\pm7$ 850 1.7 $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }21\,000$ 7.5

B361-NH3 21 $^{\rm h}$ 10 $^{\rm m}$ 33 $\hbox{$.\!\!^{\rm s}$ }$ 7 47 $\hbox{$^\circ$ }$ 12 $\hbox{$^\prime$ }$ 46 $\hbox{$^{\prime\prime}$ }$ 350 $90\pm10$ 130 1.6 $35\,000\pm3\,500$ 25.

**Table 3:** Cold dense cores with no IRAS emission
Core	Coordinates	d	$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~peak}}$ ⁽²⁾	$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ ⁽³⁾	$M^{\mbox{\tiny 4200~AU}}$ ⁽⁴⁾	$R_{\mbox{\tiny out}}$ ⁽⁵⁾	$M^{\mbox{\tiny\mbox{$R_{\mbox{\tiny out}}$ }}}$ ⁽⁶⁾
name ⁽¹⁾	$\alpha_{\rm 1950}$	$\delta_{\rm 1950}$	(pc)	(mJy/beam)	(mJy)	( $M_\odot$ )	(AU)	( $M_\odot$ )
L1489-NH3	04 $^{\rm h}$ 01 $^{\rm m}$ 45 $\hbox{$.\!\!^{\rm s}$ }$ 7	26 $\hbox{$^\circ$ }$ 11 $\hbox{$^\prime$ }$ 10 $\hbox{$^{\prime\prime}$ }$	140	$55\pm5$	510	1.0	$15\,000\pm 3\,000$	4.
L1495N-NH3	04 $^{\rm h}$ 10 $^{\rm m}$ 45 $\hbox{$.\!\!^{\rm s}$ }$ 0^*	28 $\hbox{$^\circ$ }$ 05 $\hbox{$^\prime$ }$ 40 $\hbox{$^{\prime\prime}$ }$ ^*	140	$(45\pm15)$ ^*	$\sim$ 500	$\sim$ 1.0	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }14\,000$	>5.0^*
K04169-NW	04 $^{\rm h}$ 16 $^{\rm m}$ 47 $\hbox{$.\!\!^{\rm s}$ }$ 4	27 $\hbox{$^\circ$ }$ 04 $\hbox{$^\prime$ }$ 05 $\hbox{$^{\prime\prime}$ }$	140	$50\pm15$	340	0.7	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }14\,000$	2.5
B217-NH3	04 $^{\rm h}$ 24 $^{\rm m}$ 45 $\hbox{$.\!\!^{\rm s}$ }$ 8	26 $\hbox{$^\circ$ }$ 11 $\hbox{$^\prime$ }$ 30 $\hbox{$^{\prime\prime}$ }$	140	$55\pm10$	560	1.1	$14\,000\pm 1\,500$	5.5
L1535-NE	04 $^{\rm h}$ 32 $^{\rm m}$ 36 $\hbox{$.\!\!^{\rm s}$ }$ 3	24 $\hbox{$^\circ$ }$ 03 $\hbox{$^\prime$ }$ 14 $\hbox{$^{\prime\prime}$ }$	140	$100\pm7$	850	1.7	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }21\,000$	7.5
B361-NH3	21 $^{\rm h}$ 10 $^{\rm m}$ 33 $\hbox{$.\!\!^{\rm s}$ }$ 7	47 $\hbox{$^\circ$ }$ 12 $\hbox{$^\prime$ }$ 46 $\hbox{$^{\prime\prime}$ }$	350	$90\pm10$	130	1.6	$35\,000\pm3\,500$	25.

Notes: (1) The "NH3'' suffix refers to Benson & Myers (1989); "NE'' and "NW" correspond to new dust cores. (2) to (4) Same as in Table 2. (5) Estimated outer radius. (6) Total mass within $R_{\mbox{\tiny out}}$ . ^* The characteristics of L1495N-NH3 are more uncertain as this source was incompletely mapped.

3.1 Circumstellar mass estimates

Since dust continuum emission is largely optically thin at 1.3 mm, our bolometer maps should primarily reflect the dust column density distribution within the observed circumstellar envelopes. If the dust properties and the gas-to-dust ratio are uniform, the 1.3 mm flux density $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~beam}}$ measured in a single beam should even be directly proportional to the total (gas + dust) beam-averaged column density along the line of sight: $\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~beam}}$ }\, \propto \: \k13 \; \B13 \: \times <N\h2>\mbox{$_{\mbox{\tiny beam}}$ }$ , where 13 is the dust opacity per unit mass column density at $\lambda = 1.3$ mm, and 13 is the Planck function for a dust temperature $T_{\mbox{\tiny dust}}$ (see, e.g., MAN98 for a complete equation). Accordingly, the integrated flux density is directly related to the total mass of emitting material. Column 6 of Table 2 gives the circumstellar mass contained within a radius of $4\,200$ AU of each object, derived from the 1.3 mm flux density integrated over a $30\hbox{$^{\prime\prime}$ }\times(d/140~{\rm pc})^{-1}$ radius circle, $\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ }$ (listed in Col. 5), as follows:

$\displaystyle \mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }$	=	$\displaystyle \frac{\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ }\; d^{2}}{\k13 \; \B13}$
	$\textstyle \simeq$	$\displaystyle 5.3~10^{-3}\ \mbox{$M_\odot$ }\times \left(\frac {\mbox{$S_{\mbox... ...\tiny ~int}}$ }}{\mbox{10~mJy}}\right) \left(\frac {d}{\mbox{140~pc}} \right)^2$
		$\displaystyle \times \left(\frac {\k13}{0.01\,\mbox{$\mbox{cm}^{2} \, \mbox{g}^... ...^{-1} \left(\frac {<\mbox{$T_{\mbox{\tiny dust}}$ }>}{15~\mbox{K}}\right)^{-1}.$	(1)

For consistency with previous work (e.g. AM94, AWM96, MAN98), we adopted dust opacities per unit (gas + dust) mass column density of $\k13=0.005\;\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ , $\k13=0.01\;\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ , and $\k13=0.02~\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ for starless cores, envelopes of Class 0/Class I protostars, and disks around Class II sources, respectively. These opacities correspond to the values recommended by Henning et al. (1995) assuming a gas-to-dust mass ratio of 100. Considering the likely evolution of the gas-to-dust mass ratio (cf. Ciolek & Mouschovias 1996) and of the dust properties themselves (Henning et al. 1995), the adopted opacities are believed to be uncertain by a factor of $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ } 2$ on either side of the quoted values. This is in agreement with models of dust in protostellar cores (e.g. Ossenkopf & Henning 1994), laboratory measurements (Agladze et al. 1996), and recent cross-comparisons with dust extinction observations (Kramer et al. 1999).

The value $<\mbox{$T_{\mbox{\tiny dust}}$ }>$ used for the dust temperature in Eq. (1) corresponds to a mass-weighted average calculated up to a radius of $4\,200$ AU (i.e., an angular radius of $30\hbox{$^{\prime\prime}$ }\times(d/140~{\rm pc})^{-1}$ ) and for a centrally-heated sphere with a $\rho (r) \propto r^{-2}$ density gradient ( $<\mbox{$T_{\mbox{\tiny dust}}$ }>$ would decrease by only $14\%$ if a $\rho(r) \propto r^{-1.5}$ density gradient were adopted instead). In the case of unresolved sources, a similar weighted average temperature was calculated, but only up a radius of $800~{\rm AU}\times (d/140~{\rm pc})$ (i.e. HPBW $/2 \simeq 5.5\hbox{$^{\prime\prime}$ }$ ). The radial temperature profile discussed in Sect. 4.3 below was assumed. In practice, this means that we adopted $\mbox{$<\mbox{$T_{\mbox{\tiny dust}}$ }>_{4\,200\;\rm AU}$ }= 15\ \mbox{K}$ for the envelopes surrounding the low-luminosity protostars of Taurus and $\mbox{$<\mbox{$T_{\mbox{\tiny dust}}$ }>_{4\,200\;\rm AU}$ }= 20\ \mbox{K}$ for the more luminous isolated IRAS globules and Perseus protostars. We assumed $<T_{\rm dust}> = 10$ K for the starless cores and $<T_{\rm dust}>_{800~\rm AU} = 30$ K for the unresolved YSO sources.

The reason why we chose a fiducial radius of $4\,200$ AU for the circumstellar mass in Eq. (1) and Table 2 is that this roughly corresponds 1) to the head of the expansion wave for a 10⁵-yr old protostar in the inside-out collapse scenario if the sound speed is $\mbox{$a_{\mbox{\tiny s}}$ }\sim 0.2$ km s^-1 (i.e. $\mbox{$T_{\mbox{\tiny cloud}}$ }\sim 10$ K), and 2) to an angular radius of 30 $^{\prime\prime}$ at the distance of Taurus which is comparable to the radius of the IRAS and ISO beams at $60\ \mu$ m.

For the entire sample of 27 Taurus candidate protostars (including peculiar Class Is), the median mass enclosed within 4200 is $\overline{\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }}(\r4200)\sim 0.074~\mbox{$M_\odot$ }$ . This value is not much larger than the typical disk mass found for classical T Tauri stars (Beckwith et al. 1990) or embedded Class II sources (AM94). In contrast, the 16 Taurus sources of Table 2 with spatially resolved emission are bona-fide protostars with significantly more massive circumstellar structures (envelopes/disks): $\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }\sim 0.07-0.9\ \mbox{$M_\odot$ }$ , corresponding to a median mass $\overline{\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }}(\r4200) \sim 0.28\ \mbox{$M_\odot$ }$ . The bona-fide protostars observed in Perseus and Bok globules have even larger circumstellar masses: $\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }\sim 0.3{-}5\ \mbox{$M_\odot$ }$ and $\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }\sim 0.3{-}4\ \mbox{$M_\odot$ }$ , respectively.

3.2 Envelope versus disk mass

A priori, the integrated fluxes listed in Table 2 include contributions from both the protostellar envelope and the circumstellar disk: $\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ }= S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~env}} + S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~disk}}$ . The disk contribution must be properly assessed if an accurate estimate of the envelope mass is desired.

Predictions made in the framework of the standard theory of isolated protostars suggest that the millimeter continuum flux should be dominated by emission from the envelope rather than from the disk, when observed at the resolution of the IRAM 30 m telescope (e.g. Terebey et al. 1993; Galli 1995). In agreement with these predictions, the median flux concentration $\mbox{$S^{\mbox{\tiny 11\hbox{$^{\prime\prime}$ }}}/S^{\mbox{\tiny 60\hbox{$^{\prime\prime}$ }}}$ }\sim 30\%$ estimated for the bona-fide protostars of our sample suggests that $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }70\%$ of the integrated flux density $\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ }$ arises from the envelope. Millimeter interferometric observations by, e.g., Hogerheijde et al. (1997) and Motte et al. (2001) provide estimates of the disk component $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~disk}}$ for several bona-fide protostars in Taurus, and confirm that the integrated flux density measured at the 30 m telescope arises primarily from the envelope: $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~disk}}/\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~int}}$ }(\r4200) \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }10\%$ . A similar conclusion holds in Perseus for the Class 0 protostars NGC 1333-IRAS 4A and NGC 1333-IRAS 4B which, albeit barely resolved at the $11\hbox{$^{\prime\prime}$ }$ - $13\hbox {$^{\prime \prime }$ }$ resolution of the 30 m and JCMT telescopes (cf. Table 2 and Sandell et al. 1991), are $\sim$ 8 times stronger than when observed with the CSO-JCMT interferometer (Lay et al. 1995). More generally, the disk contribution is estimated to be $\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }10\%$ for 8 of the 9 Perseus protostars of our sample (Motte et al. 2001; Looney et al. 2000).

The above discussion suggests that $\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }$ should be a good approximation of the envelope mass within $4\,200$ AU for all the "self-embedded'' sources, even when the exact disk contribution is unknown. In the following, we will thus assume $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }\sim \mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }$ for all the protostars with spatially resolved envelopes (see Col. 7 of Table 2).

By contrast, the disk can sometimes contribute a large fraction of the peak flux density $\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~peak}}$ }$ measured in an 11 $\hbox{$^{\prime\prime}$ }$ beam. For the "peculiar'', unresolved Class I sources of our sample, most of the circumstellar material may be in a disk, with $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~disk}}/\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~peak}}$ }\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }100\%$ (see discussion in Sect. 5.2.3 below). In these cases, the masses listed in Table 2 provide only upper limits to the actual envelope masses: $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }<\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny 4200~AU}}$ }$ .

4 Radial structure analysis

In this section, we describe our method of deriving the radial density structure of a circumstellar envelope from the observed intensity profile at 1.3 mm, and then apply this method to each source of Table 2.

4.1 Radial intensity profiles

The 1.3 mm continuum emission mapped around each YSO is first averaged in circular annuli centered at the peak position. This yields a mean radial intensity profile, $S(\theta)$ , where $\theta$ is the angular radius from source center. Depending on the local environment (cf. Col. 8 of Table 2), a fraction of the map has to be masked in order to avoid including emission from neighboring sources such as the fragments apparent in Figs. 1-2. When the map results from the combination of several coverages, we choose the best coverage to derive the intensity profile and make an accurate modeling (see Appendix). The resulting mean radial profiles are shown in Figs. 3a-g and 11a-l for Taurus embedded YSOs, in Figs. 4a-d and 12a-c for isolated globules, and in Figs. 4e-h and 12e-h for Perseus protostars. The radial profiles of several starless cores are also shown in Figs. 3h, 11m-p and 12d. (Figs. 11 and 12 are only available in electronic form at http://www.edpsciences.org.)

$\begin{figure} \par\includegraphics[angle=270,width=17.5cm,clip]{ms10015f3abcd.eps}\par\includegraphics[angle=270,width=17.5cm,clip]{ms10015f3efgh.eps}\end{figure}$

Figure 3: Radial intensity profiles of the environment of 7 embedded YSOs ( a-g) and 1 starless core ( h). Column density estimates assuming $\k13=0.01\;\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ and $\mbox{$T_{\mbox{\tiny dust}}$ }=15\$ K are shown on the right axis of each profile (in h): $\k13=0.005\;\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ and $\mbox{$T_{\mbox{\tiny dust}}$ }=10\$ K). The observed profiles (solid curves) are compared with simulated model profiles (dotted curves) and with the 30 m beam (dashed curve). In a) and c-e), two source profiles are shown, before (upper solid curve) and after (lower solid curve) subtraction of the disk component observed by the IRAM Plateau de Bure interferometer at 1.4 mm (Motte et al. 2001); the latter should correspond to the profile of the envelope alone. The input models are all circularly symmetric with infinite power-law profiles, $I(\theta )\propto \theta ^{-m}$ (see Appendix). Unlike YSO envelope profiles, the profile of the starless core L1535-NE (in h) is not consistent with a single power-law model. See complementary Fig. 11 on-line

$\begin{figure} \par\includegraphics[angle=270,width=17.5cm,clip]{ms10015f4abcd.eps}\par\includegraphics[angle=270,width=17.5cm,clip]{ms10015f4efgh.eps}\end{figure}$

Figure 4: Same as Fig. 3 for 4 isolated globules ( a-d) and 4 Perseus protostars ( e-h). Column density estimates assume $\k13=0.01\;\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ and $\mbox{$T_{\mbox{\tiny dust}}$ }=20$ K. In g,h), two source profiles are shown, before (upper solid curve) and after (lower solid curve) subtraction of the disk component observed by the IRAM PdBI interferometer at 1.4 mm (Motte et al. 2001). See complementary Fig. 12 on-line

These radial intensity profiles trace the underlying source column density profiles (see Sect. 3.1 and Eq. (1) of MAN98), although they also depend on the temperature gradient: $S(\theta)\propto N\h2(\theta)\times T(\theta)$ in the Rayleigh-Jeans approximation of the Planck function. Since one expects both $N\h2(\theta)$ and $T(\theta)$ to behave roughly as power-laws over a wide range of angular radii $\theta$ (see Sect. 1 above and Sect. 4.3 below), it is natural to compare the derived radial profiles with those of circularly-symmetric, power-law intensity models of the form $I(\theta )\propto \theta ^{-m}$ .

As shown by Adams (1991), the same power-law intensity distribution, $\tilde{I}(\theta)\propto \theta^{-m}$ , remains after convolution with a Gaussian beam, provided that the profile is examined at radii greater than one full beamwidth from the center (i.e., $\theta \geq 11\hbox{$^{\prime\prime}$ }$ in our case). There is, however, a major complication due to the dual-beam scanning technique, which is addressed by the simulation analysis presented in Appendix. This analysis indicates that a finite-sized, dual-beam scan/map behaves roughly like a high-pass spatial frequency filter suppressing emission on scales larger than the size of the scan/map. In practice, this entails a loss of flux density at large radii in the simulated profiles compared with the intrinsic profiles (see Fig. 7a in Appendix). In order to properly interpret the intensity profile measured toward a given protostellar envelope, we have run an input grid of power-law envelope models through a complete simulation of the mapping and data-reduction processes adapted to this particular source (see, e.g., Fig. 7b in Appendix). We can then estimate the intrinsic power-law index m of the source radial intensity profile (along with its typical uncertainty) by comparison with our output grid of simulated model profiles (cf. Figs. 3-4). The "best-fit'' power-law indices m are listed in Col. 3 of Table 4 for all the sources with spatially-resolved envelope emission. These indices apply to the main portion of the observed intensity profile (see the range of angular radii listed in Col. 2 of Table 4). We give an estimate of the envelope outer radius $\mbox{$R_{\mbox{\tiny out}}$ }$ in Col. 7 of Table 4 whenever there is evidence that the power-law regime breaks down in the outer part of the intensity profile.

Most of the sources are spatially extended and have radial intensity profiles that can be fitted reasonably well over the majority of their extent by one of our simulated $I(\theta )\propto \theta ^{-m}$ models with m = 0.4-1.8. Several observed profiles appear to steepen or merge into some cloud emission beyond a finite radius, $\mbox{$R_{\mbox{\tiny out}}$ }$ (see, e.g., Figs. 3f, 4d, and 4g). The presence of background emission from the ambient cloud is sometimes noticeable in the maps themselves (see, e.g., TMR1 in Fig. 1k). The mean column density we estimate for such background emission is $N\h2 \sim 2{-}7~10^{21}~\mbox{$\mbox{cm}^{-2}$ }$ around Taurus protostars and Bok globules (assuming $\mbox{$T_{\mbox{\tiny dust}}$ }=15\$ K and 20 K, respectively), compared to a column density of envelope material ranging from $N\h2 \sim 5~10^{21}~\mbox{$\mbox{cm}^{-2}$ }$ to $N\h2 \sim 5~10^{23}~\mbox{$\mbox{cm}^{-2}$ }$ . In Perseus, the background has $N\h2 \sim 10^{22}~\mbox{$\mbox{cm}^{-2}$ }$ , while the envelopes reach $N\h2 \sim 10^{24}~\mbox{$\mbox{cm}^{-2}$ }$ (if $\mbox{$T_{\mbox{\tiny dust}}$ }=20$ K).

By contrast, the peculiar Class I sources with compact emission in the maps (cf. Sect. 3) have intensity profiles roughly consistent with the effective point spread function of the 30 m telescope at 1.3 mm (see, e.g., Fig. 3g). This is reminiscent of the radial intensity profiles observed toward Class II sources (cf. AM94).

Finally, we note here that the radial intensity profiles of the cold cores/condensations of Table 3 are flatter than our simulated $I(\theta )\propto \theta ^{-m}$ models with m = 0.5 in their inner regions (i.e., at $r \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }6\,000\$ AU, where we measure $m \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.1$ - see the example of L1535-NE in Fig. 3h). This is reminiscent of the pre-stellar cloud cores studied by AWM96 and Ward-Thompson et al. (1999).

Table 4: Results of the radial profile analysis for the spatially resolved envelopes
Adopted $\theta$ $m(\theta)^{(1)}$ $\theta_{\mbox{\tiny isoth}}$ ⁽²⁾ $q(\theta)^{(3)}$ p $R_{\mbox{\tiny out}}$ $\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny\mbox{$R_{\mbox{\tiny out}}$ }}}$ }^{(4)}$ Additional sources

source name range ( $\hbox{$^{\prime\prime}$ }$ ) =m+1-q (AU) ( $M_\odot$ ) of uncertainty

L1551-IRS5 20 $^{\prime\prime}$ -65 $^{\prime\prime}$ $1.5\pm0.3$ 110 $^{\prime\prime}$ 0.4 $2.1\pm0.4$ $9\,100\pm700$ ? 1.5 $^{\mbox{\tiny 25K}}$

L1551-NE 11 $^{\prime\prime}$ -60 $^{\prime\prime}$ $1\pm0.3$ 51 $^{\prime\prime}$ 0.4 $1.6\pm0.4$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }8\,500$ 1.1 $^{\mbox{\tiny 25K}}$

K04113 11 $^{\prime\prime}$ -55 $^{\prime\prime}$ $1.8\pm1$ 26 $^{\prime\prime}$ 0.4 $2.4\pm1$ $8\,000\pm2\,000$ ? 0.4

L1527 11 $^{\prime\prime}$ -120 $^{\prime\prime}$ $1\pm0.4^*$ 26 $^{\prime\prime}$ $\sim$ 0 $2.0\pm0.5$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }17\,000$ 1.7 outflow cavity

K04166 11 $^{\prime\prime}$ -105 $^{\prime\prime}$ $1\pm0.2$ 11 $^{\prime\prime}$ $-0.2\pm 0.2$ $2.2\pm0.5$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }15\,000$ 1.0

K04169 11 $^{\prime\prime}$ -90 $^{\prime\prime}$ $0.8\pm0.2$ 18 $^{\prime\prime}$ 0 $1.8\pm0.3$ $13\,000\pm1\,500$ ? 1.1

T04191 11 $^{\prime\prime}$ -70 $^{\prime\prime}$ $0.8\pm0.4$ 15 $^{\prime\prime}$ 0 $1.8\pm0.5$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }10\,000$ 0.45

IRAM 04191 11 $^{\prime\prime}$ -100 $^{\prime\prime}$ $0.6\pm0.1$ 8 $^{\prime\prime}$ $-0.2\pm 0.2$ $1.8\pm0.4$ $14\,000\pm 1\,500$ ? 1.4 $^{\mbox{\tiny 12.5K}}$

T04325 11 $^{\prime\prime}$ -80 $^{\prime\prime}$ $1.0\pm0.6^*$ 20 $^{\prime\prime}$ 0 $2.0\pm0.7$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }11\,000$ 0.7 within a dense core

TMR1 11 $^{\prime\prime}$ -60 $^{\prime\prime}$ $0.8\pm0.4$ 40 $^{\prime\prime}$ 0.4 $1.4\pm0.5$ $8\,500\pm 1\,500$ ? 0.4

M04381 11 $^{\prime\prime}$ -30 $^{\prime\prime}$ $1.1\pm0.3^*$ 17 $^{\prime\prime}$ 0 $2.1\pm0.4$ $3\,900\pm700$ ? 0.16 within cloud

M04248 11 $^{\prime\prime}$ -80 $^{\prime\prime}$ $0.7\pm0.5^*$ 13 $^{\prime\prime}$ 0 $1.7\pm0.6$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }11\,000$ 0.75 elliptical envelope

K04181+2654 11 $^{\prime\prime}$ -50 $^{\prime\prime}$ $1.2\pm0.6^*$ 15 $^{\prime\prime}$ 0 $2.2\pm0.7$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }7\,000$ 0.16 elliptical envelope

L1157-MM 11 $^{\prime\prime}$ -45 $^{\prime\prime}$ $1.5\pm0.2$ 22 $^{\prime\prime}$ 0 $2.2\pm0.4^*$ $20\,000\pm2\,000?$ 6.5 deprojection

L483-MM 11 $^{\prime\prime}$ -90 $^{\prime\prime}$ $0.4\pm0.3^*$ 54 $^{\prime\prime}$ $0.2\pm0.2$ $1.2\pm0.6$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }18\,000$ 4. elliptical envelope

L588 11 $^{\prime\prime}$ -55 $^{\prime\prime}$ $1.5\pm 0.5$ ? $0.2\pm0.2$ $2.3\pm0.8$ $11\,000\pm2\,000?$ 0.8

B335 11 $^{\prime\prime}$ -120 $^{\prime\prime}$ $1.2\pm0.3^*$ 20 $^{\prime\prime}$ 0 $2.2\pm 0.4$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }30\,000$ 2.5 outflow interaction

L723-MM 11 $^{\prime\prime}$ -40 $^{\prime\prime}$ $1.7\pm0.3$ 17 $^{\prime\prime}$ 0 $2.5\pm0.5^*$ $12\,000\pm3\,000?$ 1.2 deprojection

B361 11 $^{\prime\prime}$ -40 $^{\prime\prime}$ $1.2\pm0.2$ 18 $^{\prime\prime}$ 0 $2.0\pm0.4^*$ $14\,000\pm2\,000?$ 0.9 deprojection

NGC 1333-IRAS4A 11 $^{\prime\prime}$ -50 $^{\prime\prime}$ $1.8\pm0.3$ 31 $^{\prime\prime}$ $0.2\pm0.2$ $2.6\pm0.6$ $17\,000\pm5\,000?$ 8. $^{\mbox{\tiny 35K}}$

L1448-N 11 $^{\prime\prime}$ -35 $^{\prime\prime}$ $1.7\pm0.2$ 32 $^{\prime\prime}$ 0.4 $2.1\pm0.4^*$ $10\,000\pm1\,500?$ 6 deprojection

L1448-C 11 $^{\prime\prime}$ -25 $^{\prime\prime}$ $1.6\pm0.2$ 27 $^{\prime\prime}$ 0.4 $2.0\pm0.4^*$ $7\,500\pm600?$ 2.5 deprojection

NGC 1333-IRAS2 11 $^{\prime\prime}$ -35 $^{\prime\prime}$ $1.7\pm0.3$ 61 $^{\prime\prime}$ 0.4 $2.0\pm0.5^*$ $12\,000\pm2\,000?$ 2.5 $^{\mbox{\tiny 30K}}$ deprojection

L1448-NW 11 $^{\prime\prime}$ -40 $^{\prime\prime}$ $1.3\pm0.3$ 16 $^{\prime\prime}$ $0.2\pm0.2$ $1.8\pm0.7^*$ $13\,000\pm3\,000?$ 3.5 deprojection

IRAS 03282 11 $^{\prime\prime}$ -40 $^{\prime\prime}$ $1.6\pm0.4^*$ 12 $^{\prime\prime}$ 0 $2.3\pm0.6^*$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }12\,000$ 2.5 $^{\mbox{\tiny 15K}}$ deprojection

HH211-MM 11 $^{\prime\prime}$ -45 $^{\prime\prime}$ $1.3\pm0.5^*$ $<37\hbox{$^{\prime\prime}$ }$ $0.2\pm0.2$ $2.1\pm0.6$ $\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ } 13\,000$ 2.5 "cometary'' globule

**Table 4:** Results of the radial profile analysis for the spatially resolved envelopes
Adopted	$\theta$	$m(\theta)^{(1)}$	$\theta_{\mbox{\tiny isoth}}$ ⁽²⁾	$q(\theta)^{(3)}$	p	$R_{\mbox{\tiny out}}$	$\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny\mbox{$R_{\mbox{\tiny out}}$ }}}$ }^{(4)}$	Additional sources
source name	range		( $\hbox{$^{\prime\prime}$ }$ )		=m+1-q	(AU)	( $M_\odot$ )	of uncertainty
L1551-IRS5	20 $^{\prime\prime}$ -65 $^{\prime\prime}$	$1.5\pm0.3$	110 $^{\prime\prime}$	0.4	$2.1\pm0.4$	$9\,100\pm700$ ?	1.5 $^{\mbox{\tiny 25K}}$
L1551-NE	11 $^{\prime\prime}$ -60 $^{\prime\prime}$	$1\pm0.3$	51 $^{\prime\prime}$	0.4	$1.6\pm0.4$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }8\,500$	1.1 $^{\mbox{\tiny 25K}}$
K04113	11 $^{\prime\prime}$ -55 $^{\prime\prime}$	$1.8\pm1$	26 $^{\prime\prime}$	0.4	$2.4\pm1$	$8\,000\pm2\,000$ ?	0.4
L1527	11 $^{\prime\prime}$ -120 $^{\prime\prime}$	$1\pm0.4^*$	26 $^{\prime\prime}$	$\sim$ 0	$2.0\pm0.5$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }17\,000$	1.7	outflow cavity
K04166	11 $^{\prime\prime}$ -105 $^{\prime\prime}$	$1\pm0.2$	11 $^{\prime\prime}$	$-0.2\pm 0.2$	$2.2\pm0.5$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }15\,000$	1.0
K04169	11 $^{\prime\prime}$ -90 $^{\prime\prime}$	$0.8\pm0.2$	18 $^{\prime\prime}$	0	$1.8\pm0.3$	$13\,000\pm1\,500$ ?	1.1
T04191	11 $^{\prime\prime}$ -70 $^{\prime\prime}$	$0.8\pm0.4$	15 $^{\prime\prime}$	0	$1.8\pm0.5$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }10\,000$	0.45
IRAM 04191	11 $^{\prime\prime}$ -100 $^{\prime\prime}$	$0.6\pm0.1$	8 $^{\prime\prime}$	$-0.2\pm 0.2$	$1.8\pm0.4$	$14\,000\pm 1\,500$ ?	1.4 $^{\mbox{\tiny 12.5K}}$
T04325	11 $^{\prime\prime}$ -80 $^{\prime\prime}$	$1.0\pm0.6^*$	20 $^{\prime\prime}$	0	$2.0\pm0.7$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }11\,000$	0.7	within a dense core
TMR1	11 $^{\prime\prime}$ -60 $^{\prime\prime}$	$0.8\pm0.4$	40 $^{\prime\prime}$	0.4	$1.4\pm0.5$	$8\,500\pm 1\,500$ ?	0.4
M04381	11 $^{\prime\prime}$ -30 $^{\prime\prime}$	$1.1\pm0.3^*$	17 $^{\prime\prime}$	0	$2.1\pm0.4$	$3\,900\pm700$ ?	0.16	within cloud
M04248	11 $^{\prime\prime}$ -80 $^{\prime\prime}$	$0.7\pm0.5^*$	13 $^{\prime\prime}$	0	$1.7\pm0.6$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }11\,000$	0.75	elliptical envelope
K04181+2654	11 $^{\prime\prime}$ -50 $^{\prime\prime}$	$1.2\pm0.6^*$	15 $^{\prime\prime}$	0	$2.2\pm0.7$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }7\,000$	0.16	elliptical envelope
L1157-MM	11 $^{\prime\prime}$ -45 $^{\prime\prime}$	$1.5\pm0.2$	22 $^{\prime\prime}$	0	$2.2\pm0.4^*$	$20\,000\pm2\,000?$	6.5	deprojection
L483-MM	11 $^{\prime\prime}$ -90 $^{\prime\prime}$	$0.4\pm0.3^*$	54 $^{\prime\prime}$	$0.2\pm0.2$	$1.2\pm0.6$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }18\,000$	4.	elliptical envelope
L588	11 $^{\prime\prime}$ -55 $^{\prime\prime}$	$1.5\pm 0.5$	?	$0.2\pm0.2$	$2.3\pm0.8$	$11\,000\pm2\,000?$	0.8
B335	11 $^{\prime\prime}$ -120 $^{\prime\prime}$	$1.2\pm0.3^*$	20 $^{\prime\prime}$	0	$2.2\pm 0.4$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }30\,000$	2.5	outflow interaction
L723-MM	11 $^{\prime\prime}$ -40 $^{\prime\prime}$	$1.7\pm0.3$	17 $^{\prime\prime}$	0	$2.5\pm0.5^*$	$12\,000\pm3\,000?$	1.2	deprojection
B361	11 $^{\prime\prime}$ -40 $^{\prime\prime}$	$1.2\pm0.2$	18 $^{\prime\prime}$	0	$2.0\pm0.4^*$	$14\,000\pm2\,000?$	0.9	deprojection
NGC 1333-IRAS4A	11 $^{\prime\prime}$ -50 $^{\prime\prime}$	$1.8\pm0.3$	31 $^{\prime\prime}$	$0.2\pm0.2$	$2.6\pm0.6$	$17\,000\pm5\,000?$	8. $^{\mbox{\tiny 35K}}$
L1448-N	11 $^{\prime\prime}$ -35 $^{\prime\prime}$	$1.7\pm0.2$	32 $^{\prime\prime}$	0.4	$2.1\pm0.4^*$	$10\,000\pm1\,500?$	6	deprojection
L1448-C	11 $^{\prime\prime}$ -25 $^{\prime\prime}$	$1.6\pm0.2$	27 $^{\prime\prime}$	0.4	$2.0\pm0.4^*$	$7\,500\pm600?$	2.5	deprojection
NGC 1333-IRAS2	11 $^{\prime\prime}$ -35 $^{\prime\prime}$	$1.7\pm0.3$	61 $^{\prime\prime}$	0.4	$2.0\pm0.5^*$	$12\,000\pm2\,000?$	2.5 $^{\mbox{\tiny 30K}}$	deprojection
L1448-NW	11 $^{\prime\prime}$ -40 $^{\prime\prime}$	$1.3\pm0.3$	16 $^{\prime\prime}$	$0.2\pm0.2$	$1.8\pm0.7^*$	$13\,000\pm3\,000?$	3.5	deprojection
IRAS 03282	11 $^{\prime\prime}$ -40 $^{\prime\prime}$	$1.6\pm0.4^*$	12 $^{\prime\prime}$	0	$2.3\pm0.6^*$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }12\,000$	2.5 $^{\mbox{\tiny 15K}}$	deprojection
HH211-MM	11 $^{\prime\prime}$ -45 $^{\prime\prime}$	$1.3\pm0.5^*$	$<37\hbox{$^{\prime\prime}$ }$	$0.2\pm0.2$	$2.1\pm0.6$	$\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ } 13\,000$	2.5	"cometary'' globule

Notes: ⁽¹⁾ Power-law index of the radial intensity profile $\mbox{$S_{\mbox{\tiny 1.3~mm}}(\theta)$ }$ over the angular range of Col. 2. ⁽²⁾ Angular radius beyond which heating by the central source is negligible. ⁽³⁾ Power-law index of the radial temperature profile $T(\theta)\propto \theta^{-q}$ over the angular range of Col. 2. ⁽⁴⁾ Total circumstellar mass within the radius $\mbox{$R_{\mbox{\tiny out}}$ }$ of Col. 7 (see Sect. 3.1 for assumed dust opacity and temperature). Star markers in Col. 3 or Col. 6 indicate that additional sources of uncertainty have been taken into account (see Col. 9).

4.2 Factors influencing the derivation of the envelope radial profile

4.2.1 Disk component

In order to derive the intrinsic profile of the envelope, a central point source corresponding to the possible contribution of a compact, unresolved disk should in principle be subtracted out from the bolometer-array data. However, the disk contribution to the single-dish peak flux density appears to be small for the bona-fide protostars of our sample. Based on interferometric measurements, Motte et al. (2001) estimate $S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~disk}}/\mbox{$S_{\mbox{\tiny 1.3~mm}}^{\mbox{\tiny ~peak}}$ }\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }30\%$ for 7 Taurus YSOs and 5 Perseus protostars (see also Sect. 3.2). We have simulated the effect of an unresolved disk component of this magnitude and checked that it does not affect the radial intensity profile measured for $\theta> 11\hbox{$^{\prime\prime}$ }$ (see Fig. 8a in Appendix). We conclude that the disk has a negligible influence on our analysis of the envelope radial profile, even in the case of the Perseus protostars with compact envelopes (cf. Sect. 3.2). To illustrate this point, Figs. 3-4 and Figs. 11-12 show the estimated envelope radial profile before and after subtraction of the disk component when the latter is known.

4.2.2 Background cloud

In the presence of filamentary background cloud emission, an intrinsically spherical envelope can artificially look non spherical. The maps of K04169, M04248, and IRAS 03282 (in Figs. 1d, 1f, and 2d) may provide examples of this. In principle, the power-law index $m_{\mbox{\tiny obs}}$ of the observed intensity profile should then be corrected by a term $\epsilon_{\mbox{\tiny back}}$ to yield the intrinsic index of the source envelope: $m_{\mbox{\tiny env}} = m_{\mbox{\tiny obs}} + \epsilon_{\mbox{\tiny back}}$ , where $\epsilon_{\mbox{\tiny back}} >0$ when the effective background emission is positive. (If there is relatively strong background emission just outside the mapped region, part of it may aliased as a negative signal in the restored image, in which case $\epsilon_{\mbox{\tiny back}} < 0$ .) In order to minimize the magnitude of this effect, we measured the intensity profile of each source in the parts of the map least perturbed by any cloud (or companion) emission. For K04169, M04248, and IRAS 03282, we restricted our analysis to sectors perpendicular to the large-scale filamentary emission apparent in Fig. 1d, Fig. 1f, and Fig. 2d. Any remaining background emission should thus be weak compared to the envelope emission itself. We have simulated the observation of a power-law envelope embedded in a Gaussian background of FWHM size 0.5 pc and peak column density $N\h2 \sim 10^{21}$ - $10^{22}\,\mbox{$\mbox{cm}^{-2}$ }$ . These simulations suggest that $\epsilon_{\mbox{\tiny back}}$ is negligible (i.e., $\epsilon_{\mbox{\tiny back}} \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.1$ ) for most sources (see Appendix). In the case of T04325 which lies in the middle of strong emission from the dense core L1535-NE (cf. Fig. 1j), we estimate $\epsilon_{\mbox{\tiny back}} \simeq 0.3$ .

4.2.3 Non spherical envelopes, perturbation
by the outflow

The millimeter dust emission of several sources is clearly not circularly symmetric but displays an elliptical or even more complex morphology (e.g. L1527, B335, HH211-MM). The asymmetries seen toward L1527 and B335 appear to be directly related to the influence of their bipolar outflows. The map of L1527 (Fig. 1l) shows a clear cross-like pattern probably marking the walls of a bipolar cavity excavated by the outflow, which is reminiscent of what is seen at $730\ \mu$ m toward L1551-IRS5 (Ladd et al. 1995). The dust emission mapped around B335 is elongated perpendicular to the outflow axis (Fig. 2a). These bar-like or cross-like enhancements of 1.3 mm dust emission may originate from compression and/or heating of the envelope by the outflow (cf. Gueth et al. 1997). The resulting uncertainties can be estimated by comparing the radial profiles obtained in different quadrants of the maps (see Col. 3 of Table 4). The radial profile averaged over the northern quadrant of the L1527 envelope and the profile measured perpendicular to the B335 outflow are very close to the corresponding circularly averaged profiles: $m_{\mbox{\tiny perp}} = m_{\mbox{\tiny circ}} \pm 0.2$ . In Table 4, we thus give the power-law indices measured for the circularly-averaged intensity profiles of L1527 and B335, but add an extra $\Delta m =0.2$ term to the uncertainty estimated from the power-law fit.

4.3 Assessment of the dust temperature distribution

Assuming that central heating by the inner accreting protostar dominates the thermal balance of the envelope, the dust temperature is expected to decrease outward. More precisely, one expects a radial temperature profile of the form $T(r) \propto r^{-q}$ with $q \approx 0.4$ in the region where the envelope is optically thin to the bulk of the infrared radiation (e.g. Emerson 1988; Butner et al. 1990). In practice, one thus expects (see, e.g., Terebey et al. 1993):

$\begin{displaymath}\mbox{$T_{\mbox{\tiny dust}}$ }(r, \mbox{$L_\star$ }) \approx... ...( \frac{\mbox{$L_\star$ }}{1~\mbox{$L_\odot$ }} \right)^{0.2}, \end{displaymath}$

(2)

where the stellar luminosity $\mbox{$L_\star$ }$ can be approached by the bolometric luminosity listed in Table 1. Evidently, this temperature distribution is valid only up to the radius where $\mbox{$T_{\mbox{\tiny dust}}$ }(r, \mbox{$L_\star$ })$ reaches the typical dust temperature of the parent ambient cloud, i.e., $\mbox{$T_{\mbox{\tiny cloud}}$ }\sim 10$ K (appropriate to Taurus-Auriga, Perseus, and most isolated globules, see e.g. Myers & Benson 1983). The preceding equation implies that the radius, $\mbox{$R_{\mbox{\tiny isoth}}$ }$ , beyond which $\mbox{$T_{\mbox{\tiny dust}}$ }(r> \mbox{$R_{\mbox{\tiny isoth}}$ }) \approx \mbox{$T_{\mbox{\tiny cloud}}$ }$ , is approximately given by:

$\begin{displaymath}\mbox{$R_{\mbox{\tiny isoth}}$ }(\mbox{$L_\star$ }) \simeq \m... ...( \frac{\mbox{$L_\star$ }}{1~\mbox{$L_\odot$ }} \right)^{0.5}. \end{displaymath}$

(3)

The angular radius $\mbox{$\theta_{\mbox{\tiny isoth}}$ }$ corresponding to $\mbox{$R_{\mbox{\tiny isoth}}$ }$ is listed in Col. 4 of Table 4. According to these estimates, most of the envelopes observed in Taurus and isolated globules are likely to be roughly isothermal (at the temperature of the ambient cloud) on the spatial scales sampled by our maps [i.e., for $r > 1\,500~{\rm AU}\times (d/140~{\rm pc})$ ]. On the other hand, we expect central heating to play a significant role in shaping the intensity profiles of the more luminous protostars of Perseus.

For very low luminosity and/or very young accreting protostars, central heating may be completely negligible, and the envelope thermal structure may be dominated by external heating from cosmic rays and the interstellar radiation field (e.g. Goldsmith & Langer 1978; Neufeld et al. 1995), as is probably the case for pre-stellar cores. Gas-grain collisions are expected to maintain the gas and dust temperatures reasonably well coupled to each other, at least for densities $n\h2 \lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }10^5\, \cm3$ (e.g. Ceccarelli et al. 1996). Calculations taking these processes into account show that externally-heated envelopes/cores are likely to be cooler in their inner regions than their parent $\sim$ 10 K molecular clouds (e.g. Falgarone & Puget 1985; Masunaga & Inutsuka 1999; Evans et al. 2001). Masunaga & Inutsuka (1999) find envelope temperatures of $\sim$ 6 K and $\sim$ 10 K at radii of $\sim$ 1000 AU and $\sim$ 10000 AU, respectively, from the center of a $\sim$ 0.1 $L_\odot$ protostar that has just entered the accretion phase. This would correspond to an effective temperature index $q \approx -0.4$ in the range of radii probed by our 1.3 mm observations. Such an outward increase in the envelope temperature is likely to apply to the lowest luminosity protostars of our Taurus sample, e.g., IRAM 04191 and K04166. We have thus adopted $q=-0.2\pm 0.2$ for these objects (see Col. 5 of Table 4).

4.4 Inferred radial density gradients

The intrinsic intensity profiles obtained in Sect. 4.1 can now be used to constrain the radial density profiles of the observed circumstellar envelopes provided that some assumptions are made about their 3-D geometry and temperature structure (see Sect. 4.3).

For an infinite, spherically-symmetric envelope, a simple asymptotic relation exists between the column density profile (see Figs. 3,4) and the underlying radial density gradient (e.g. Arquilla & Goldsmith 1991; YC91; Adams 1991): $N\h2(\bar{r}) \propto r \times \rho(r)$ . Consequently, in the Rayleigh-Jeans regime, spheroidal envelopes with power-law density and temperature gradients (i.e., $\rho(r)\propto r^{-p}$ and $T(r) \propto r^{-q}$ , respectively) are expected to have specific intensity profiles of the form $I(\bar{r})\propto \bar{r}^{-m}$ with m = p + q -1 as a function of projected radius $\bar{r}$ . The power-law density index, p=m+1-q, derived in this way from the "best-fit'' index of the radial intensity profile, m, is given in Col. 6 of Table 4, assuming the temperature index qlisted in Col. 5. Given the morphologies observed in the plane of the sky (see Figs. 1-2), the assumption that the envelopes are roughly spheroidal should be adequate, at least as a first approximation (see, however, Sect. 4.2.3 above and Col. 9 of Table 4). Even in the case of an ellipsoidal envelope, our approach should still yield a correct estimate for the angle-averaged density profile. On the other hand, the density and temperature gradients in the envelopes may not be correctly described by single power-laws over the full range of radii sampled by our observations. If, instead, the density and temperature gradients are represented by series of broken power-laws, then the preceding, simple formula relating p, m, and q will no longer be strictly valid in the transition regions owing to convergence effects. A correction term must be added: $p = m+1-q-\epsilon_{\mbox{\tiny proj}}$ . In particular, this is the case for a finite-sized sphere where the density drops to 0 beyond some radius $\mbox{$R_{\mbox{\tiny out}}$ }$ (e.g. Arquilla & Goldsmith 1985; YC91). Our maps indicate that $\theta_{\mbox{\tiny out}} \lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }70\hbox{$^{\prime\prime}$ }$ (i.e. $\mbox{$R_{\mbox{\tiny out}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }10\,000$ AU at 140 pc) may be a typical value for the outer radius of protostellar envelopes in Taurus and Bok globules (see Col. 7 in Table 4). The correction term due to deprojection effects is then small ( $\epsilon_{\mbox{\tiny proj}} \approx 0.1$ , see Appendix) and is partly compensated for by the presence of background emission (see Sect. 4.2.2). In these cases, we have thus neglected $\epsilon_{\mbox{\tiny proj}}$ and have conservatively estimated the error bar on p as $\Delta p = \Delta m + \Delta q + 0.1$ . For the protostars with compact envelopes (i.e., $\theta_{\mbox{\tiny out}} \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }40\hbox{$^{\prime\prime}$ }$ in Col. 2 of Table 4), we have used $\epsilon_{\mbox{\tiny proj}} \approx 0.3$ (or 0.2 when a significant background cloud exists) and $\Delta p = \Delta m + \Delta q +0.2$ (see Col. 6 of Table 4).

Taking the various uncertainties into account (see also Sects. 4.2 and 4.3 above), the power-law index of the radial density gradient is found to be $p \sim 1.5-2$ from $r \sim 1\,000\,-\,5\,000$ AU to $r \sim 10\,000\,-\,50\,000$ AU for the spatially resolved envelopes of Taurus YSOs and Bok globules. In several cases, the power-law density structure appears to break down at a finite radius beyond which the envelope merges with the ambient cloud: $\overline{\mbox{$R_{\mbox{\tiny out}}$ }} \lower.5ex\hbox{$\; \buildrel > \over \sim \;$ } 10\,000$ AU for the Taurus YSOs and $\overline{\mbox{$R_{\mbox{\tiny out}}$ }} \lower.5ex\hbox{$\; \buildrel > \over \sim \;$ } 16\,000$ AU for the Bok globules. The power-law density analysis is more uncertain for the compact protostellar envelopes of Perseus for which we estimate $p=(2-2.5)\pm 0.6$ and $\overline{\mbox{$R_{\mbox{\tiny out}}$ }} \sim 10\,000$ AU. For the "peculiar'' Class I sources which are essentially unresolved in our maps (see Fig. 3g and Col. 7 of Table 2), the radius of any envelope, if present at all, must be much smaller, $\mbox{$R_{\mbox{\tiny out}}$ }\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }1\,500$ AU. The nature of these peculiar Class I sources is discussed in Sect. 5.2.3 below.

5 Discussion

5.1 Structure of protostellar envelopes and comparison with collapse models

The millimeter continuum maps and radial profiles presented in Sects. 3 and 4 allow us to test, in Sect. 5.1.2 below, several theoretical predictions which we first summarize in Sect. 5.1.1.

5.1.1 Detailed model predictions

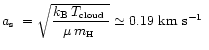In the self-similar collapse theory of Shu and co-workers, the instantaneous structure of a protostellar dense core is primarily determined by the position of the expansion wavefront (see Sect. 1). For a typical cloud temperature $\mbox{$T_{\mbox{\tiny cloud}}$ }\approx 10\$ K (e.g. Myers & Benson 1983), the isothermal sound speed is $\mbox{$a_{\mbox{\tiny s}}$ }= \sqrt{\displaystyle\frac{k_{\rm B}\, \mbox{$T_{\m... ...d}}$ }}{\mu\, \mbox{$m_{\mbox{\tiny H}}$ }}} \simeq 0.19\ {\mbox{km s$^{-1}$ }}$ (where $k_{\rm B}$ is the Boltzman constant, $\mu = 2.33$ the mean molecular weight, and $\mbox{$m_{\mbox{\tiny H}}$ }$ the mass of atomic hydrogen). At the distance of the Taurus cloud, the head of the expansion wave should be located at angular radii $\theta_{\rm inf}\sim 3\hbox{$^{\prime\prime}$ }$ , $\sim$ $30\hbox{$^{\prime\prime}$ }$ and $\sim$ $5\hbox{$^\prime$ }$ , when t=10⁴ yr, t=10⁵ yr, and t=10⁶ yr, respectively. A power-law density profile of the form $\rho(r)\propto r^{-p}$ is expected, with $p \approx 1.5$ inside the expansion wavefront, and $p \approx 2$ further out. More generally, the work of Whitworth & Summers (1985) shows that, during the protostellar phase (i.e., $t \geq 0$ ), all isothermal similarity solutions converge at small radii toward a free-fall density profile of the type $\rho (r,t) = \frac{1}{4\pi} \, (\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }/2G)^{1/2} \: r^{-3/2} \: t^{-1/2}$ , where $\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }= w_0\, \mbox{$a_{\mbox{\tiny s}}$ }^3 / G$ is the accretion rate with w₀ ranging from 0.975 for the Shu case to $\sim$ 47 for the Larson-Penston case.

Hence, in all self-similar isothermal models, the mass enclosed within a given radius of the infall envelope should roughly scale as $\mbox{$M_{\mbox{\tiny env}}$ }(r < R) \propto t^{-1/2}$ , where t is the age of the central protostar (i.e., the time elapsed since point mass formation). When the sound speed is $\mbox{$a_{\mbox{\tiny s}}$ }= 0.19\ {\mbox{km s$^{-1}$ }}$ , the envelope masses predicted by the Shu model are: $\mbox{$M_{\mbox{\tiny env}}$ }(\r4200, t\rm = 10^4\rm\, yr\rm )\simeq 0.35~\mbox{$M_\odot$ }$ , $\mbox{$M_{\mbox{\tiny env}}$ }(\r4200, t\rm = 10^5\rm\, yr\rm )\simeq 0.19~\mbox{$M_\odot$ }$ , and $\mbox{$M_{\mbox{\tiny env}}$ }(\r4200, t\rm = 10^6\rm\, yr\rm )\simeq 0.03~\mbox{$M_\odot$ }$ (see e.g. Fig. 5a). For t > 0, the envelope masses are expected to be a factor $\sim$ 7 larger in the Larson-Penston solution than in the Shu model. For comparison, at point mass formation (t=0), the mass enclosed by the (static) SIS at $\mbox{$T_{\mbox{\tiny cloud}}$ }=10\$ K is $M_{\mbox{\tiny SIS}}(r<R\rm ) = \frac{2\:a^2}{G} \: R \simeq 0.37~\mbox{$M_\odot$ }$ for $R=4\,200\rm\ AU$ , while the mass enclosed by the (dynamic) Larson-Penston flow is $\sim$ 4.4 times larger. In the magnetized case, a similar overdensity factor exists between the dynamical similarity solution of Contopoulos et al. (1998) around t = 0 and the (equilibrium) singular isothermal magnetic disk (see discussion in Basu 1998). When the collapse initial conditions are not self-similar but correspond to pressure-truncated Bonnor-Ebert isothermal spheres, the (inner) density profile is expected to approach that of the Larson-Penston similarity solution near point mass formation ( $t \lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }0$ ) but to relax toward the Shu density profile at later times, until the expansion wavefront reaches the finite outer radius of the cloud core (see Foster & Chevalier 1993).

In the alternative, non-isothermal description of the collapse by McLaughlin & Pudritz (1996, 1997), based on a logotropic equation of state of the type $P/P_{\rm c} = 1 + A\,$ ln $(\rho/\rho_{\rm c})$ (where $A \sim 0.2$ , and $P_{\rm c}$ and $\rho_{\rm c}$ are the central values of the pressure and density), the initial conditions are taken to be a singular logotropic sphere with $\rho(r) = (A P_{\rm c}/2\pi G)^{1/2}r^{-1}$ , truncated by external pressure at some outer radius $\mbox{$R_{\mbox{\tiny out}}$ }$ . When the collapse of such a logotrope is initiated (by, e.g., a small increase in external pressure), the density distribution also approaches a free-fall $\rho(r) \propto r^{-1.5}$ power-law inside the head of the expansion wave. The envelope mass enclosed within $R = 4\,200$ AU remains essentially constant during a first "redistribution'' phase. For a critical logotrope of total mass $M_{\mbox{\tiny tot}} \sim 92~\mbox{$M_\odot$ }$ and outer radius $\mbox{$R_{\mbox{\tiny out}}$ }\simeq 19\,000$ AU, this phase lasts for approximately 10⁶ yr and the enclosed mass is $\mbox{$M_{\mbox{\tiny env}}$ }(\r4200, t\rm = 0-10^6\rm\ yr\rm )\simeq 0.15~\mbox{$M_\odot$ }$ , assuming the nominal parameters adopted by McLaughlin & Pudritz (i.e., $\mbox{$T_{\mbox{\tiny cloud}}$ }=10\$ K and a surface pressure $P_{\rm s} = 1.3~10^{5} \times k_{\rm B}~\cm3~\mbox{K}$ ). Thereafter, the stellar mass increases roughly as $\mbox{$M_\star$ }(t) \propto t^4$ and the envelope mass decreases accordingly [ $\mbox{$M_{\mbox{\tiny env}}$ }(t)=M_{\mbox{\tiny tot}}-\mbox{$M_\star$ }(t)$ ], until all the mass has been accreted and the accretion phase is terminated at $t\simeq 2.5~10^6$ yr. The accretion history predicted by this model is thus very different from that of the Shu et al. model.

5.1.2 Comparison with observations

Given observational uncertainties, the power-law density structure derived in Sect. 4 for the envelopes of bona-fide protostars in Taurus and Bok globules [ $\rho(r)\propto r^{-p}$ with $p \simeq 1.5-2$ ] is consistent with that expected for either a SIS (p = 2) or a free-fall configuration (p = 1.5). In the context of the standard protostellar model, the median circumstellar mass $\overline{\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }} \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.074~\mbox{$M_\odot$ }$ estimated for our complete sample of Taurus candidate protostars corresponds to a collapse age of $t\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }3~10^5$ yr. This value is in rough agreement with the typical lifetime inferred for Taurus Class I sources based on statistical arguments ( $t \simeq 1-2~10^5\$ yr - see, e.g., KHSS90). Furthermore, the median envelope mass of the "bona-fide'' Class I/0 protostars of Taurus, $\overline{\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }}\sim 0.28\ \mbox{$M_\odot$ }$ , is within a factor of $\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }2$ of $M_{\mbox{\tiny SIS}}(r<4\,200\, \rm AU)$ , suggesting that these objects are still well into the main accretion phase with estimated collapse ages $t \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }5~10^4$ yr. By contrast, the median mass measured for the 11 undetected or unresolved Class I sources of Taurus (see e.g. Fig. 3g), is very low ( $\overline{\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }} < 0.01\ \mbox{$M_\odot$ }$ ), and corresponds to a very old collapse age $t\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }9~10^6$ yr. This is much longer than the estimated lifetime of the protostellar embedded phase, implying that the peculiar Class I sources cannot be genuine protostars. Altogether, except perhaps for these peculiar sources (see also Sect. 5.2.1 below), our Taurus results are in fairly good agreement with the predictions of the standard collapse model.

On the other hand, the envelopes of Class 0 protostars in both Perseus and isolated globules tend to be a factor of $\sim$ 2 to $\sim$ 12 more massive than is predicted by the standard model, even if very young collapse ages are assumed: $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }\simeq 0.6-5\ \mbox{$M_\odot$ }$ is measured, while a maximum of $M_{\mbox{\tiny SIS}}(\r4200)\simeq 0.4\ \mbox{$M_\odot$ }$ is expected. As the gas temperature in the initial cloud core cannot be much larger than 10 K (e.g. Ladd et al. 1994), such large masses cannot be explained in the SIS picture unless non-thermal sources of support are included. A factor of $\sim$ 2 increase in mass can be accommodated by the standard model if a significant (static) magnetic field is present (e.g. Li & Shu 1996). In principle, turbulence may also contribute to the support of the initial dense core (e.g. Myers & Fuller 1992). However, the small-scale condensations or "kernels'' corresponding to the progenitors of protostars in star-forming clusters (e.g. MAN98) appear to be essentially "coherent'', i.e., largely devoid of turbulence (Goodman et al. 1998; Myers 1998; Belloche et al. 2001). We conclude that variants of the standard model can probably account for the masses measured in most Bok globules but are clearly insufficient to explain the $> 1.5\ \mbox{$M_\odot$ }$ envelopes observed toward L1157-MM and the Class 0 objects of Perseus. The most likely explanation in the latter cases is that the collapse started from non-singular initial conditions, resulting in a nonequilibrium density configuration similar to the Larson-Penston flow near point mass formation (see Sect. 5.1.1 above). Such a conclusion, which is consistent with the large accretion/ejection rates inferred for Perseus Class 0 objects (Bontemps et al. 1996 - hereafter BATC96), could be tested if direct observational constraints on the infall velocity field of these sources are obtained: large infall velocities are indeed expected.

In contrast to isothermal models, the logotropic model of McLaughlin & Pudritz (1997) accounts only marginally for our Taurus results: the radial density structure we observe ( $p \simeq 1.5-2$ ) is somewhat steeper than the predictions (i.e., p=0.5-1.5). The disagreement is most serious for the Taurus YSOs with the most massive envelopes, namely the young Class 0 objects IRAM 04191, K04166, and L1527, which have $p= (1.8-2.2)\pm 0.5$ , while p=0.5-1 is expected at $t \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ } 10^6$ yr in this model. Moreover, the envelope mass predicted by the nominal critical model of McLaughlin & Pudritz during the collapse [ $\mbox{$M_{\mbox{\tiny env}}$ }(\r4200) \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.15\ \mbox{$M_\odot$ }$ at most] is significantly lower than that implied by our observations in both Taurus and isolated globules. The case of B335 is discussed by McLaughlin & Pudritz (1997) who conclude that this object may correspond to a $1\ \mbox{$M_\odot$ }$ collapsing logotrope at the end of its accretion phase. However, our measurements of the envelope mass [ $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }\simeq 0.9\ \mbox{$M_\odot$ }$ ] and power-law density index [ $p=2.2\pm 0.4$ ] are not consistent with such a model which predicts $\mbox{$M_{\mbox{\tiny env}}$ }(\r4200)\ll 0.034\ \mbox{$M_\odot$ }$ and p=1.5.

Furthermore, none of the low-mass pre-stellar cores studied in detail up to now has a density structure consistent with a pressure-truncated logotrope (Bacmann et al. 2000).

5.2 Protostellar evolution in Taurus-Auriga

5.2.1 The ${\mathsfsl M}_{\mathsf {env}} - {\mathsfsl L}_{\mathsf {bol}}$ evolutionary diagram

As shown by AM94 and Saraceno et al. (1996), the envelope mass ( $\mbox{$M_{\mbox{\tiny env}}$ }$ ) vs. bolometric luminosity ( $\mbox{$L_{\mbox{\tiny bol}}$ }$ ) diagram can be used as a practical evolutionary diagram for embedded YSOs. While $\mbox{$M_{\mbox{\tiny env}}$ }$ provides a measure of the mass reservoir that remains to be accreted, the bolometric luminosity $\mbox{$L_{\mbox{\tiny bol}}$ }$ may be used to estimate the mass of the central star, $\mbox{$M_\star$ }$ , via plausible mass-luminosity relations for protostars (see AM94 for details). Conceptually, Class 0 protostars were defined as YSOs with $\mbox{$M_{\mbox{\tiny env}}$ }> \mbox{$M_\star$ }$ by AWB93. Because of uncertainties in, e.g., the mass-luminosity relationship, the actual observational boundary between Class 0 and Class I objects is not a well-defined border line but a border zone. The original Class 0 criterion given by AWB93, namely $\mbox{$L_{\mbox{\tiny submm}}^{\mbox{\tiny$\lambda > 350~\mu$ m}}$ }/\mbox{$L_{\mbox{\tiny bol}}$ }> 0.5\%$ , is based on a linear mass-luminosity relationship (i.e., $\mbox{$M_\star$ }\propto \mbox{$L_{\mbox{\tiny bol}}$ }$ , as expected if $\mbox{$L_{\mbox{\tiny bol}}$ }$ derives only from accretion onto a star with a fixed $\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }/\mbox{$R_\star$ }$ ratio) and typical dust properties for converting $\mbox{$L_{\mbox{\tiny submm}}^{\mbox{\tiny$\lambda > 350~\mu$ m}}$ }$ to $\mbox{$M_{\mbox{\tiny env}}$ }$ (cf. AWB93 and AM94). In terms of the $\mbox{$M_{\mbox{\tiny env}}$ }$ - $\mbox{$L_{\mbox{\tiny bol}}$ }$ diagram, this roughly corresponds to $\mbox{$M_{\mbox{\tiny env}}$ }/\mbox{$L_{\mbox{\tiny bol}}$ }> 0.1\ \mbox{$M_\odot$ }/\mbox{$L_\odot$ }$ . In practice, the status of sources lying close to this formal border line is uncertain, and only YSOs with $\mbox{$L_{\mbox{\tiny submm}}^{\mbox{\tiny$\lambda > 350~\mu$ m}}$ }/\mbox{$L_{\mbox{\tiny bol}}$ }>> 0.5\%$ are considered as bona-fide Class 0 objects (see AWB2000).

$\begin{figure} \par\includegraphics[angle=0,width=8.8cm,clip]{ms10015f5.eps}\end{figure}$

Figure 5: $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }$ vs. $\mbox{$L_{\mbox{\tiny bol}}$ }$ diagram in Taurus. Bona-fide protostars are shown as (open and filled) circles (for Class 0 and Class I objects, respectively), while peculiar Class I sources are denoted by open star-like markers. The solid straight lines are two $\mbox{$M_\star$ }$ - $\mbox{$L_{\mbox{\tiny bol}}$ }$ relations marking the conceptual border zone between the Class 0 stage ( $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }> \mbox{$M_\star$ }$ ) and the Class I stage ( $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }< \mbox{$M_\star$ }$ ): $\mbox{$M_\star$ }\propto \mbox{$L_{\mbox{\tiny bol}}$ }$ (cf. AWB93 and AM94) and $\mbox{$M_\star$ }\propto \mbox{$L_{\mbox{\tiny bol}}$ }^{0.6}$ as suggested by the time-dependent accretion scenario of the text (see also AWB2000). Two distinct sets of evolutionary tracks (solid curves) are shown, based on: a) A constant accretion rate, $\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }\approx 2~10^{-6}~\mbox{$M_\odot\: \mbox{yr}^{-1}$ }$ , as in the standard model. Arrows mark time steps from $t=10^4\$ yr to $t=4 \times 10^5\$ yr. (The dotted curves illustrate the magnitude of the observational uncertainties on $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }$ .) b) A time-dependent accretion rate, $\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }\propto \mbox{$M_{\mbox{\tiny env}}$ }(t)$ , as described in the text. Small arrows are plotted on the tracks every 10⁴ yr, big arrows when $50\%$ and $90\%$ of the initial core mass has been accreted

Our $\mbox{$M_{\mbox{\tiny env}}$ }$ - $\mbox{$L_{\mbox{\tiny bol}}$ }$ diagram for the embedded YSOs of Taurus is displayed in Figs. 5a,b, along with two sets of evolutionary tracks. The values of $\mbox{$M_{\mbox{\tiny env}}$ }$ (from Sect. 3.2) and $\mbox{$L_{\mbox{\tiny bol}}$ }$ (from the literature) used in this diagram can be found in Tables 1 and 2, respectively. Rather than the total masses detected in the maps, we have preferred to use our estimates of the inner envelope mass, $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }$ (see Sect. 3.2). Our maps suggest that the envelopes of bona-fide protostars in Taurus have a power-law density structure up to a fairly large radius, $\mbox{$R_{\mbox{\tiny out}}$ } \sim 4\,000$ - $17\,000$ AU (cf. Col. 7 of Table 4). But the total mass measured within $\mbox{$R_{\mbox{\tiny out}}$ }$ , which has a median value $\overline{\mbox{$M_{\mbox{\tiny c$\star$ }}^{\mbox{\tiny\mbox{$R_{\mbox{\tiny out}}$ }}}$ }}\sim 0.83\ \mbox{$M_\odot$ }$ , is unlikely to be entirely accreted by the central object. As pointed out by, e.g., Ladd et al. (1998), the outflow will probably disperse a significant fraction of this mass. Our map of the L1527 envelope, which shows some evidence for a bipolar cavity oriented along the outflow axis (Fig. 1l), is consistent with this view. As the star formation efficiency in a single isolated core is expected to be $\sim$ 30% on theoretical grounds (Matzner & Mckee 2000), we believe that the initial core mass within $R = 4\,200$ AU should provide a better indicator of the final stellar mass than the total core mass.

The first set of evolutionary tracks, shown in Fig. 5a, corresponds to the predictions of the standard protostellar model (e.g. Adams et al. 1987) and assumes that $\mbox{$L_{\mbox{\tiny bol}}$ }= \mbox{$L_{\mbox{\tiny acc}}$ }= (G\,\mbox{$M_\star$ }\,\mbox{$\dot{M}_{\mbox{\tiny acc}}$ })/\mbox{$R_\star$ }$ , with $\mbox{$a_{\mbox{\tiny s}}$ }=0.19~{\mbox{km s$^{-1}$ }}$ (i.e., $\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }\simeq 1.6~10^{-6}~\mbox{$M_\odot\: \mbox{yr}^{-1}$ }$ ) and $\mbox{$R_\star$ }= 3\ \mbox{$R_\odot$ }$ .

The second set of evolutionary tracks (Fig. 5b) shows the predictions of the accretion scenario advocated by BATC96 and AWB2000, in which protostars form from dense cores with finite initial masses, M₀, and both the envelope mass and the accretion rate are assumed to decline exponentially with time according to $\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }(t) = \mbox{$M_{\mbox{\tiny env}}$ }(t)/\tau = M_0\, \exp(-t/\tau)/\tau$ , where $\tau\approx 10^5$ yr is a characteristic time. Such a decline of $\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }$ is consistent with the decrease of outflow power observed from Class 0 to Class I protostars (BATC96), and is theoretically expected in the case of non-singular collapse initial conditions (e.g. Foster & Chevalier 1993; HAB97). The tracks of Fig. 5b further assume that the observed bolometric luminosities result from a combination of accretion and stellar contributions: $\mbox{$L_{\mbox{\tiny bol}}$ }= G\mbox{$M_\star$ }\mbox{$\dot{M}_{\mbox{\tiny acc}}$ }/\mbox{$R_\star$ }+ \mbox{$L_\star$ }$ , where $\mbox{$R_\star$ }(\mbox{$M_\star$ }, \mbox{$\dot{M}_{\mbox{\tiny acc}}$ }) \approx 3\, \mbox{$R_\odot$ }$ is the stellar radius and $\mbox{$L_\star$ }(\mbox{$M_\star$ }, \mbox{$\dot{M}_{\mbox{\tiny acc}}$ })$ the stellar luminosity on the birthline for PMS stars (Stahler 1988).

It can be seen that the "standard'' tracks based on the self-similar theory of Shu et al. (1987) account relatively well for the locations of the bona-fide protostars of Taurus in the $\mbox{$M_{\mbox{\tiny env}}$ }$ - $\mbox{$L_{\mbox{\tiny bol}}$ }$ diagram (see Fig. 5a). Furthermore, there is a good continuity between Class 0 and (bona-fide) Class I objects: In regions of isolated star formation, Class 0 objects (open circles in Fig. 5a) may merely correspond to extreme versions of bona-fide Class I sources (filled circles). A similar conclusion was reached by HAB97 based on a discussion of the outflow properties (see Fig. 10 of HAB97). In this respect, it is noteworthy that more than half of the bona-fide Class I sources of Fig. 5 lie above the solid straight lines marking the border zone between $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }> \mbox{$M_\star$ }$ and $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }< \mbox{$M_\star$ }$ in the diagram: They match the conceptual definition of the Class 0 stage given by AWB93 (see above). Our observations are thus consistent with the idea that all of the bona-fide Class 0 and Class I objects of Fig. 5 are in the main accretion phase of YSO evolution.

Despite this reasonably good agreement, two problems should be pointed out. First, as noticed by Kenyon et al. (1993a, hereafter KCH93) and summarized by Hartmann (1998), the accretion luminosities predicted by the standard model tend to be larger than the observed bolometric luminosities by up to an order of magnitude: the luminosity predicted at a typical collapse age of $\sim$ 2 10⁵ yr is $\mbox{$L_{\mbox{\tiny acc}}$ }\sim 5\, \mbox{$L_\odot$ }$ , while the median Class I/0 luminosity in our sample is $\overline{\mbox{$L_{\mbox{\tiny bol}}$ }} \sim 0.8\, \mbox{$L_\odot$ }$ . This discrepancy is quite severe even though it can be reduced by a factor of $\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }2$ if non-spherical accretion effects and wind driving are properly taken into account (cf. Shu et al. 1996). The solution proposed by KCH93 is that envelope material does not fall directly onto the central star but piles up in a disk whose radius is substantially larger than the stellar radius, thereby reducing the infall luminosity. It remains to be seen, however, whether short episodes of high disk accretion ("FU Ori'' outbursts) can be made frequent enough to maintain $M_{\rm disk} \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.1\, \mbox{$M_\odot$ }$ throughout the embedded phase, as measured by millimeter interferometers (e.g. Terebey et al. 1993; Looney et al. 2000).

A second problem with the evolutionary tracks of the standard model is that they do not account for the properties of the peculiar Class I sources identified here (open star markers in Fig. 5a). In spite of their Class I infrared SEDs (Adams et al. 1987; KCH93) and low bolometric temperatures ( $\overline{\mbox{$T_{\mbox{\tiny bol}}$ }}=350$ K according to Chen et al. 1995), these objects cannot be interpreted as accreting protostars in the framework of the inside-out collapse model. Possible interpretations are given in Sect. 5.2.3 below.

The tracks assuming an exponential decrease in the rate of envelope dissipation with time (Fig. 5b) explain the luminosities of the bona-fide Class 0/I protostars better than do the standard tracks (see also HAB97 and Myers et al. 1998), and account even marginally for the locations of the peculiar Class I sources.

Although obviously idealized, this time-dependent accretion scenario hints that the peculiar Class I sources may correspond to low-mass objects at the very end of the protostellar accretion phase. In this view, they would be the descendants of the lowest mass bona-fide protostars of Fig. 5. Physically, an exponential termination of the accretion phase may result from the finite mass reservoir available in the initial pre-collapse core. Indeed, our 1.3 mm continuum maps suggest that, even in Taurus, the initial core is bounded with $\mbox{$R_{\mbox{\tiny out}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }10\,000$ AU (see, e.g., Fig. 3f). When the collapse expansion wave reaches $\mbox{$R_{\mbox{\tiny out}}$ }$ (which occurs at $t = \mbox{$R_{\mbox{\tiny out}}$ }/\mbox{$a_{\mbox{\tiny s}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }2.5~10^5\$ yr in the standard picture), the circumstellar evolution is likely to change drastically in character: the central YSO should enter a phase of residual accretion and its remnant envelope may be quickly dispersed by the outflow. The peculiar Class I sources may be representative of this late accretion phase.

5.2.2 Comparison with $\rho$ Ophiuchi

For direct comparison with Fig. 5, we show in Fig. 6 the $\mbox{$M_{\mbox{\tiny env}}$ }$ - $\mbox{$L_{\mbox{\tiny bol}}$ }$ diagram constructed for the self-embedded YSOs of $\rho$ Ophiuchi using data from AM94, MAN98, and Wilking et al. (1989). Since the protostars of $\rho$ Ophiuchi are surrounded by compact, finite-sized envelopes (cf. MAN98), $\mbox{$M_{\mbox{\tiny env}}$ }$ is here simply taken to be the total mass enclosed within a relatively well-defined envelope outer radius (cf. AM94). The same evolutionary tracks as in Fig. 5 are superposed. In this case, a clear contrast between Class 0 and Class I objects is apparent. The standard tracks, which would imply a continuum of protostars rather than two separate classes, do not fit the $\rho$ Oph diagram and cannot account for the observed Class I sources with $\mbox{$M_{\mbox{\tiny env}}$ }\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.1\, \mbox{$M_\odot$ }$ and $\mbox{$L_{\mbox{\tiny bol}}$ }\sim$ 1-2 $\mbox{$L_\odot$ }$ .

On the other hand, the time-dependent accretion tracks explain all of the $\rho$ Oph objects reasonably well. It is also noteworthy that the sources are on average more luminous (by a factor $\sim$ 3-10) in Ophiuchus than in Taurus (see also Chen et al. 1995). This, coupled with the fact that the standard accretion scenario is satisfactory in Taurus, supports the suggestion of HAB97 (see also André 1997) that embedded YSOs follow different accretion histories in $\rho$ Ophiuchi and in Taurus. This is presumably the result of a marked difference in fragmentation lengthscale between the two clouds: $\mbox{$R_{\mbox{\tiny out}}$ }\sim 3\,000$ AU in $\rho$ Oph (cf. MAN98) versus $\mbox{$R_{\mbox{\tiny out}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }10\,000$ AU in Taurus (this paper).

Comparing Fig. 5 with Fig. 6, and Fig. 1 with the $\rho$ Oph 1.3 mm maps of AM94 and MAN98, we suggest that the circumstellar evolutionary state of the peculiar Class I YSOs of Taurus may be similar to that of the typical Class I sources of Ophiuchus: in both cases, only remnant, compact envelopes are present.

$\begin{figure} \par\includegraphics[angle=0,width=8.8cm,clip]{ms10015f6.eps}\end{figure}$

Figure 6: Same as Fig. 5 for the embedded YSOs of the $\rho$ Ophiuchi main cloud (adapted from AM94). In this case, $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }$ is equivalent to the total envelope mass $\mbox{$M_{\mbox{\tiny env}}$ }$ . Note that, in contrast to the Taurus diagram, there is a gap between Class 0 and Class I objects here

5.2.3 Nature of the unresolved Class I sources

A possible interpretation of the peculiar Class I objects is that they are in fact PMS stars seen in a particular configuration and/or environment. The very weak, if not absent, outflow activity observed toward the peculiar Class I sources (see BATC96) supports this view. First, some of these sources may be viewed through a high visual extinction due to a large inclination to the line of sight (cf. Sonnhalter et al. 1995). Existing near-infrared maps of scattered light toward K04302 show a pronounced dark lane and are indeed suggestive of a TTS surrounded by a circumstellar disk seen roughly edge-on (Padgett et al. 1999; see also Lucas & Roche 1997). Second, a PMS star with a very low envelope mass could also present a Class I SED if its disk is warped by the tidal effects of a close companion (Terquem & Bertout 1993, 1996). Possible examples of this could be M04108-B, M04295, and M04489, whose estimated extinctions are moderate and which appear point-like in near-infrared images (Kenyon et al. 1993b). Third, several sources, such as M04108-B, Elias6, and HH30-IRS, are observed on the same line of sight as diffuse cloud emission (see Col. 8 of Table 2). This may produce both substantial near-IR extinction and significant far-IR (IRAS) excess resulting in a Class I SED.

On the other hand, the near-infrared spectra observed by Greene & Lada (1996) for L1489, M04295, M04489 and M04181+2655 differ from those of T Tauri stars. If the near-IR spectroscopy scheme developped by Greene & Lada (1996) is correct, M04295, M04489 and M04181+2655 should be intermediate objects between protostars and PMS stars and L1489 should be surrounded by significant envelope material. We also note that Z04260 is not strictly point-like in our 1.3 mm data (see Fig. 11k). Furthermore, millimeter interferometric mapping of L1489 (e.g. Hogerheijde et al.1997, 1998; Ohashi 1999) reveals a $\sim$ 1000 AU rotating structure with possible infall motions, which is apparently different from the more compact disks typically observed in T Tauri stars (see, e.g., Dutrey et al. 1996).

Several peculiar Class I sources may thus be highly reddened PMS stars while others could be objects in transition between protostars and T Tauri stars. These sources illustrate that the interpretation of YSO SEDs is non unique and that mapping information, preferably at several wavelengths, is crucial to get at a proper physical picture (see also Miroshnichenko et al. 1999).

5.3 Cold dense fragments undetected by IRAS

As mentioned in Sect. 3, our 1.3 mm maps reveal the presence of at least seven new dense cores/condensations in the vicinity of the targeted YSOs (see Table 3). Since these cold cores do not coincide with IRAS point sources, they are good candidates for being at either the pre-stellar stage or the Class 0 protostellar stage of evolution (cf. AWB2000). One of these objects, IRAM 04191, has been studied in more detail (AMB99) and corresponds to the first clear-cut example of a Class 0 protostar in Taurus: It has a large envelope mass ( $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }\sim 0.5\, M_\odot$ ), very low bolometric luminosity and bolometric temperature ( $\mbox{$L_{\mbox{\tiny bol}}$ }\sim 0.15\, L_\odot$ , $\mbox{$T_{\mbox{\tiny bol}}$ }\sim 18\,$ K), and features a jet-like CO outflow as well as extended infall motions. Some of the cores of Table 3 may also be associated with very young accreting protostars. On the other hand, the fact that five of these sources have flat inner intensity profiles (see Sect. 4.1 and Fig. 3h) suggests that they rather correspond to pre-stellar dense cores similar to those discussed by Ward-Thompson et al. (1994, 1999). Follow-up observations are required to assess their nature more firmly. In any event, the serendipitous discovery of these cold objects in the course of a pointed 1.3 mm mapping study of IRAS YSOs clearly emphasizes the need for deep, unbiased surveys of molecular clouds in the submillimeter band. Such surveys should soon become possible with, e.g., the Far InfraRed and Submillimeter Telescope (FIRST) of ESA.

6 Summary and conclusions

In an effort to constrain protostellar evolution and test the predictions of collapse models, we have mapped the column density structure of the circumstellar environment of 49 low-mass embedded YSOs in the dust continuum at 1.3 mm. Our sample includes all 27 Class I (and Class 0) sources presently known in Taurus, along with 9 isolated Bok globules and 9 protostars in Perseus. Our main findings may be summarized as follows:

1.: In good agreement with the predictions of the standard protostellar model of Shu et al. (1987), 16 of the Taurus Class I/0 sources are observed to be surrounded by relatively massive ( $\overline{\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }}\sim 0.3\ \mbox{$M_\odot$ }$ ), spatially extended ( $\mbox{$R_{\mbox{\tiny out}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }10\,000$ AU) circumstellar envelopes with a power-law density gradient such as $\rho (r) \propto r^{-2}$ or $\rho(r) \propto r^{-1.5}$ . These sources are consistent with being "bona-fide'' protostars, currently in their main accretion phase;
2.: Contrary to expectations, however, the 1.3 mm continuum emission mapped toward 11 Class I sources in Taurus and 1 Class I Bok globule is weak and essentially unresolved. These "peculiar'' Class I sources have very small circumstellar envelope masses, $\mbox{$M_{\mbox{\tiny env}}^{\mbox{\tiny 4200~AU}}$ }< 0.002$ - $0.04\ \mbox{$M_\odot$ }$ , implying that they cannot be genuine protostars and must be at the very end of their accretion phase. Despite their low bolometric temperatures ( $\overline{\mbox{$T_{\mbox{\tiny bol}}$ }} \sim 350$ K), they are most likely highly reddened PMS stars and/or transition objects between protostars and T Tauri stars;
3.: Like the "bona-fide'' protostars of Taurus, 8 of the 9 embedded YSOs mapped in Bok globules have circumstellar envelope properties that are consistent to first order with the standard model. The envelopes of these objects tend nevertheless to be a factor of $\sim$ 2 denser than is predicted by a purely thermal model with $\mbox{$T_{\mbox{\tiny cloud}}$ }=10\$ K. Magnetic fields may have contributed a significant fraction of the support in the corresponding pre-collapse cloud cores;
4.: By contrast, the envelopes of 8 Class 0 protostars in Perseus are found to be much denser, by a factor of 3-12, than is expected in the standard collapse model. They are also relatively compact with outer radii of only a few thousand AUs ( $\mbox{$R_{\mbox{\tiny out}}$ }\sim 10\,000$ AU). This is suggestive of a more dynamical picture in which external disturbances initiate the collapse of finite-sized cloud fragments with flat inner density profiles, and supersonic infall velocities develop during a runaway isothermal phase prior to the main accretion stage. Such a picture appears to be more appropriate than the standard model for describing individual collapse in cluster-forming cores. Direct spectroscopic measurements of the velocity field are however needed to confirm this view;
5.: In the close environment of 6 of the 24 Class I YSOs mapped in Taurus, our maps revealed the presence of previously unknown 1.3 mm continuum condensations. All are undetected in the infrared and are good candidates for being new pre-stellar cores and/or young accreting protostars. One of them coincides with the Class 0 object IRAM 04191 already discussed in AMB99. The discovery of these cold condensations shows that infrared observations can only give a partial census of star formation activity in molecular clouds (see also point 2 above), and emphasizes the need for deep, unbiased mapping surveys in the submillimeter band.

Acknowledgements

We would like to thank Roberto Neri for providing the observing parameters necessary to develop our simulation program within the NIC software. We also acknowledge the participation of Sylvie Cabrit in the early phases of this work and the contribution of Sylvain Bontemps during the last observing run. We are also grateful to Anne Dutrey, Frédéric Gueth, Stéphane Guilloteau, and Roberto Neri for their assistance in deriving disk fluxes from our Plateau de Bure interferometric observations.

$\begin{figure} \par\includegraphics[angle=270,width=16cm,clip]{ms10015f7.eps}\end{figure}$

Figure 7: a) Effect of the dual-beam observing technique on the observed radial intensity profiles. The dash-dotted curve represents an input model with $I(\theta )\propto \theta ^{-1}$ (cf. dotted line) after convolution with the beam of the telescope (dashed curve). The solid curve shows the output model profile that results from our simulation of the dual-beam observation and the various data reduction steps. b) Grid of simulated profiles for a range of input power-law models, $I(\theta )\propto \theta ^{-m}$ , with m=0.1 to 2.5

Appendix: Simulations of dual-beam scanning
observations with the bolometer array

We have developed a program that simulates, for any given input model envelope, the dual-beam maps that would be observed by the various channels of the bolometer array in the on-the-fly scanning mode. For each source, the simulation procedure uses the same "mapping geometry'' as in the real observations: same map size, integration steps (in both azimuth and elevation), absolute coordinates of map center, observing hour angle, wobbler throw, and array geometry. The procedure also accounts for any possible offset of the source with respect to map center and includes a convolution with the beam of the telescope. The simulated dual-beam maps are then reduced in exactly the same way as the real data, including baseline subtraction, flagging of any bad channel, restoration to equivalent single-beam Az-El maps, and combination/projection onto a RA-Dec grid (see, e.g., Emerson et al. 1979; Broguière et al. 1995).

These simulations allow us to assess the loss of signal which results from observing extended envelopes with the dual-beam method. As an example, Fig. 7a shows the transformation of a $I(\theta )\propto \theta ^{-1}$ input envelope model (dotted line) after convolution with the 30 m beam (dashed-dotted line) and the various observation/data reduction steps (solid line). For such an extended envelope model, the beam convolution does not modify the slope of the profile at angular radii $\theta>\$ HPBW (i.e., $11\hbox{$^{\prime\prime}$ }$ here), in agreement with the conclusions of Adams (1991). However, the observation/data reduction technique does change the shape of the radial profile (see hatched region in Fig. 7a), due to the finite size of the maps. This is because all spatial scales larger than the azimuth extent $\Delta Az$ of the maps are filtered out. The slope of the simulated output profile depends only weakly on the value of the wobbler throw as long as the latter remains small compared to the map size (in azimuth). (Note that the chop throw would be the most determinant factor in the case of on-off/jiggle-stare maps.) The array geometry and the offset of the source model with respect to map center have little influence on the simulated profile providing the map is big enough that the source is effectively imaged as a positive and a negative signal by each bolometer. Baseline subtraction also has a negligible effect as long as only low-order polynomials are taken out, namely a baseline of order 0-2 applied in time on the global image, plus a simple DC level (0-order baseline) on each map row.

$\begin{figure} \par\includegraphics[angle=270,width=16.3cm,clip]{ms10015f8.eps}\end{figure}$

Figure 8: a) Grid of simulated profiles corresponding to a $I(\theta )\propto \theta ^{-1}$ input envelope model including an unresolved central source (or disk) characterized by $S_{\mbox{\tiny disk}} / \mbox{$S_{\mbox{\tiny env}}^{\mbox{\tiny peak}}$ }= 0$ , 1, 2 and 10. b) Simulated profiles corresponding to finite-sized isothermal envelope models with $\rho (r) \propto r^{-2}$ inside an outer radius corresponding to $\theta_{\mbox{\tiny out}}=45\hbox{$^{\prime\prime}$ }$ and $70\hbox {$^{\prime \prime }$ }$

Figure 7b presents a grid of simulated model profiles based on the map geometry corresponding to our observations of L1527 (see Fig. 3c). The input models have power-law profiles of the form $I(\theta )\propto \theta ^{-m}$ with m=0.1 to 2.5 beyond an inner radius of $\theta_{\mbox{\tiny in}}=0.5\hbox{$^{\prime\prime}$ }$ . (Note that the simulated profiles for m < 2 are not sensitive to the exact value of $\theta_{\mbox{\tiny in}}$ as long as it is much smaller than the beam radius, i.e. $\theta_{\mbox{\tiny in}}<\;$ HPBW/10.) As expected, the shallower the slope of the input model, the larger the fractional loss of emission due to the dual-beam observing mode. It is thus crucial to estimate the level of this effect through simulations before a reliable comparison between observed profiles and input models can be made. Such a comparison is more uncertain in the case of envelopes with steep density gradients (e.g. $m\ge2$ in Fig. 7b), as this leads to radial intensity profiles which closely follow the shape of the beam. Although the main beam of the 30 m telescope is a relatively well known Gaussian with FWHM $\ \simeq 11\hbox{$^{\prime\prime}$ }$ at 1.3 mm, the effective error beam associated with dual-beam on-the-fly bolometer observations is more poorly characterized. In particular, the beam model proposed by Guélin (1992) from spectroscopic observations at 1 mm appears to be inconsistent with our own estimation based on bolometer mapping of strong point sources (see dashed line in Fig. 7b). Fortunately, this is not a serious problem here since the radial intensity profiles of most of our sources are well resolved and cannot be fitted by steep ( $m\geq2$ ) power-laws.

In order to simulate the effect of an inner disk component, we have added a central point source to a $I(\theta )\propto \theta ^{-1}$ power-law envelope model (see Fig. 8a). The resulting intensity profile follows the shape of the error beam at large radii when $S_{\mbox{\tiny disk}} / \mbox{$S_{\mbox{\tiny env}}^{\mbox{\tiny peak}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }5$ . (For a $I(\theta) \propto \theta^{-1.5}$ input envelope model, the same occurs when $S_{\mbox{\tiny disk}} / \mbox{$S_{\mbox{\tiny env}}^{\mbox{\tiny peak}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }3$ .) Although such large "disk-to-envelope'' ratios could apply to T Tauri stars (e.g. HL Tau), they are not observed in the case of bona-fide protostars which typically have $S_{\mbox{\tiny disk}} / \mbox{$S_{\mbox{\tiny env}}^{\mbox{\tiny peak}}$ }\lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }30\%$ (see, e.g., Looney et al. 2000; Motte et al. 2001). In most cases, the disk should thus have a negligible influence on our analysis of the envelope radial profiles at angular radii $\theta>\$ HPBW.

We have also embedded a $I(\theta )\propto \theta ^{-1}$ envelope model in a Gaussian background cloud with FWHM $\ =0.5$ pc and a cloud-to-envelope peak flux ratio of $S^{\mbox{\tiny peak}}_{\mbox{\tiny cloud}} / \mbox{$S_{\mbox{\tiny env}}^{\mbox{\tiny peak}}$ }\sim 5\%$ , corresponding to a typical ambient column density of $N\h2\sim 10^{21}-10^{22} \, \mbox{$\mbox{cm}^{-2}$ }$ . The emission of such an extended Gaussian cloud is essentially filtered out by the dual-beam observing technique. Thus, the apparent power-law index $m_{\mbox{\tiny obs}}$ of the radial profile should only be corrected by a small term $\epsilon_{\mbox{\tiny back}} \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.1$ to yield the intrinsic index of the envelope profile, i.e., $m_{\mbox{\tiny env}} = m_{\mbox{\tiny obs}} + \epsilon_{\mbox{\tiny back}}$ (see Sect. 4.2.2).

Finally, we have simulated the dual-beam observation of a finite-sized envelope with an outer radius $\mbox{$R_{\mbox{\tiny out}}$ }$ similar to the values measured from Figs. 3 and 4 (see Table 4). Typically, our observations suggest $\mbox{$R_{\mbox{\tiny out}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ } 6\times HPBW\simeq 30\%\:\Delta Az$ in Taurus and Bok globules, and $\mbox{$R_{\mbox{\tiny out}}$ }\lower.5ex\hbox{$\; \buildrel > \over \sim \;$ }3.5~HPBW \simeq 18\%\:\Delta Az$ in Perseus. According to YC91, the slopes of the intensity profiles measured on such angular scales (i.e., HPBW $\ < \theta < 3.5-6\times HPBW$ ) should be corrected by $\epsilon_{\mbox{\tiny proj}} > 0.5$ when estimating the intrinsic slopes of the density profiles (i.e., $p = m+1-q-\epsilon_{\mbox{\tiny proj}}$ ), in order to properly account for projection effects. Figure 8b shows that, due to dual-beam filtering, the effective correction term is much smaller in our case: $\epsilon_{\mbox{\tiny proj}} \lower.5ex\hbox{$\; \buildrel < \over \sim \;$ }0.1$ in Taurus and Bok globules and $\epsilon_{\mbox{\tiny proj}} \simeq 0.3$ in Perseus.

References

Adams, F. C. 1991, ApJ, 382, 544 NASA ADS
Adams, F. C., Lada, C. J., & Shu, F. H. 1987, ApJ, 312, 788 NASA ADS
Agladze, N. I., Sievers, A. J., Jones, S. A., Burlitch, J. M., & Beckwith, S. V. W. 1996, ApJ, 462, 1026 NASA ADS
André, P. 1997, in Herbig-Haro Flows and the Birth of Low-Mass Stars, IAU Symposium 182, ed. B. Reipurth, & C. Bertout (Kluwer, Dordrecht), 483
André, P., & Montmerle, T. 1994, ApJ, 420, 837 (AM94) NASA ADS
André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 (AWB93) NASA ADS
André, P., Ward-Thompson, D., & Barsony, M. 2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell (Univ. of Arizona Press, Tucson), 59 (AWB2000)
André, P., Ward-Thompson, D., & Motte, F. 1996, A&A, 314, 625 (AWM96) NASA ADS
André, P., Motte, F., & Bacmann, A. 1999, ApJL, 513, L57 (AMB99)
Anglada, G., Estalella, R., Rodriguez, L. F., et al. 1991, ApJ, 376, 615 NASA ADS
Anglada, G., Rodriguez, L. F., Canto, J., Estalella, R., & Torrelles, J. M. 1992, ApJ, 395, 494 NASA ADS
Arquilla, R., & Goldsmith, P. F. 1985, ApJ, 297, 436 NASA ADS
Bachiller, R., André, P., & Cabrit, S. 1991a, A&A, 241, L43 NASA ADS
Bachiller, R., Martín-Pintado, J., & Planesas, P. 1991b, A&A, 251, 639 NASA ADS
Bachiller, R., Terebey, S., Jarrett, T., et al. 1994, ApJ, 437, 296 NASA ADS
Bacmann, A., André, P., & Puget, J.-L. 2000, A&A, 361, 555 NASA ADS
Barsony, M., & Chandler, C. J. 1993, ApJ, 406, L71 NASA ADS
Barsony, M., Ward-Thompson, D., André, P., & O'Linger, J. 1998, ApJ, 509, 733 NASA ADS
Basu, S. 1997, ApJ, 485, 240 NASA ADS
Basu, S. 1998, ApJ, 509, 229 NASA ADS
Beckwith, S. V. W., Sargent A. I., Chini, R. S., & Güsten, R. 1990, AJ, 99, 924 NASA ADS
Beichman, C. A., Boulanger, F., & Moshir, M. 1992, ApJ, 386, 248 NASA ADS
Beichman, C. A., Myers, P. C., Emerson, J. P., et al. 1986, ApJ, 307, 337 NASA ADS
Belloche, A., André, P., & Motte, F. 2001, in From Darkness to Light, ed. T. Montmerle, & P. André, in press
Benson, P. J., & Myers, P. C. 1989, ApJS, 71, 89 NASA ADS
Bertout, C. 1989, ARA&A, 27, 351 NASA ADS
Blottiau, P., Bouquet, S., & Chièze, J.-P. 1988, A&A, 207, 24 NASA ADS
Bonnor, W. B. 1956, MNRAS, 116, 351 NASA ADS
Bontemps, S., André, P., Terebey, S., & Cabrit, S. 1996, A&A, 311, 858 (BATC96) NASA ADS
Broguière, D., Neri, R., & Sievers, A. 1995, NIC bolometer users guide (IRAM internal report)
Butner, H. M., Evans II, N. J., Lester, D. F., Levreault, R. M., & Strom, S. E. 1991, ApJ, 376, 636 NASA ADS
Butner, H. M., Evans II, N. J., Harvey, P. M., et al. 1990, ApJ, 364, 164 NASA ADS
Casali, M. M. 1986, MNRAS, 223, 341 NASA ADS
Ceccarelli, C., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 471, 400 NASA ADS
Cernicharo, J., Bachiller, R., & Duvert, G. 1985, A&A, 149, 273 NASA ADS
Chandler, C. J., & Richer, J. S. 2000, ApJ, 530, 851 NASA ADS
Chandler, C. J., Barsony, M., & Moore, T. J. T. 1998, MNRAS, 299, 789 NASA ADS
Chen, H., Myers, P. C., Ladd, E. F., & Wood, D. O. S. 1995, ApJ, 445, 377 NASA ADS
Chen, H., Grenfell, T. G., Myers, P. C., & Hughes, J. D. 1997, ApJ, 478, 295 NASA ADS
Choi, M., Evans, N. J., Gregersen, E. M., & Wang, Y. 1995, ApJ, 448, 742 NASA ADS
Ciolek, G. E., & Königl, A. 1998, ApJ, 504, 257 NASA ADS
Ciolek, G. E., & Mouschovias, T. Ch. 1996, ApJ, 468, 749 NASA ADS
Clemens, D. P., & Barvainis, R. 1988, ApJS, 68, 257 NASA ADS
Contopoulos, I., Ciolek, G. E., & Königl, A. 1998, ApJ, 504, 247 NASA ADS
Curiel, S., Raymond, J. C., Moran, J. M., Rodriguez, L. F., & Canto, J. 1990, ApJ, 365, 85
Davidson, J. A. 1987, ApJ, 315, 602 NASA ADS
Dutrey, A., Guilloteau, S., Duvert, G., et al. 1996, A&A, 309, 493 NASA ADS
Emerson, J. P. 1988, in Formation and Evolution of Low Mass Stars, ed. Dupree, & Lago, 21
Emerson, D. T., Klein, U., & Haslam, C. G. T. 1979, A&A, 76, 92 NASA ADS
Evans, N. J., Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, in preparation
Falgarone, E., & Puget, J.-L. 1985, A&A, 142, 157 NASA ADS
Foster, P. N., & Chevalier, R. A. 1993, ApJ, 416, 303 NASA ADS
Fuller, G. A., Ladd, E. F., & Hodapp, K. W. 1996, ApJ, 463, L97 NASA ADS
Galli, D. 1995, Rev. Mex. A&A (Ser. de Conf.), 1, 179
Galli, D., & Shu, F. H. 1993, ApJ, 417, 220 NASA ADS
Goldsmith, P. F., & Langer, W. D. 1978, ApJ, 222, 881 NASA ADS
Gómez, M., Hartmann, L., Kenyon, S. J., & Hewett, R. 1993, AJ, 105, 1927 NASA ADS
Goodman, A. A., Barranco, J. A., Wilner, D. J., & Heyer, M. H. 1998, ApJ, 504, 223 NASA ADS
Greene, T. P, & Lada, C. J. 1996, AJ, 112, 2184 NASA ADS
Greene, T. P., Wilking, B. A., André, P., Young, E. T., & Lada, C. J. 1994, ApJ, 434, 614 NASA ADS
Gregersen, E. M., Evans II, N. J., Zhou, S., & Choi, M. 1997, 484, 256
Griffin, M. J., & Orton, G. S. 1993, Icarus, 105, 337
Guélin, M. 1992, in The infrared and submillimetre sky after COBE, Proceedings of the NATO Advanced Study Institute, 423
Gueth, F., Guilloteau, S., Dutrey, A., & Bachiller, R. 1997, A&A, 323, 943 NASA ADS
Hartmann, L. W. 1998, Accretion Processes in Star Formation (Cambridge University Press), Chap. 4
Hartmann, L. W. 2000, in Star formation from the small to the large scale, ed. F. Favata, A. A. Kaas, & A. Wilson, ESA SP-445, in press [astro-ph/0001125]
Henning, Th., Michel, B., & Stognienko, R. 1995, Planet. Space Sci. (Special issue: Dust, molecules and backgrounds), 43, 1333 NASA ADS
Henriksen, R. N., André, P., & Bontemps, S. 1997, A&A, 323, 549 (HAB97) NASA ADS
Heyer, M. H., Snell, R. L, Goldsmith, P. F., & Myers, P. C. 1987, ApJ, 321, 370 NASA ADS
Hogerheijde, M. R., & Sandell, G. 2000, ApJ, 534, 880 NASA ADS
Hogerheijde, M. R., van Dishoeck, E. F., Blake, G. A., & van Langevelde, H. J. 1997, ApJ, 489, 293 NASA ADS
Jennings, R. E., Cameron, D. H. M., Cudlip, W., & Hirst, C. J. 1987, MNRAS, 226, 461 NASA ADS
Keene, J., & Masson, C. R. 1990, ApJ, 355, 635 NASA ADS
Kenyon, S. J., & Hartmann, L. W. 1995, ApJS, 101, 117 NASA ADS
Kenyon, S. J., Calvet, N., & Hartmann, L. 1993a, ApJ, 414, 676 (KCH93) NASA ADS
Kenyon, S. J., Hartmann, L. W., Strom, K. M., & Strom, S. E. 1990, AJ, 99, 869 (KHSS90) NASA ADS
Kenyon, S. J., Whitney, B. A., Gómez, M., & Hartmann, L. 1993b, ApJ, 414, 773 NASA ADS
Kramer, K., Alves, J., Lada, C. J., et al. 1999, A&A, 342, 257 NASA ADS
Kreysa, E, Gemünd, H. P., Gromke, J., et al. 1998, Proc. SPIE, 3357, 319
Lada, C. J. 1987, in Star forming regions, IAU Symp. 115, ed. M. Peimbert, & J. Jugaku, 1
Ladd, E. F., Fuller, G. A., & Deane, J. R. 1998, ApJ, 495, 871 NASA ADS
Ladd, E. F., Myers, P. C., & Goodman, A. A. 1994, ApJ, 433, 117 NASA ADS
Ladd, E. F., Fuller, G. A., Padman, R., Myers, P. C., & Adams, F. C. 1995, ApJ, 439, 771 NASA ADS
Ladd, E. F., Adams, F. C., Casey, S., et al. 1991, ApJ, 382, 555 NASA ADS
Larson, R. B. 1969, MNRAS, 145, 271 NASA ADS
Lay, O. P., Carlstrom, J. E., & Hills, R. E. 1995, ApJ, 452, L73 NASA ADS
Lee, C. W., & Myers, P. C. 1999, ApJS, 123, 233 NASA ADS
Li, Z.-Y. 1998, ApJ, 493, 230 NASA ADS
Li, Z.-Y., & Shu, F. H. 1996, ApJ, 472, 211 NASA ADS
Li, Z.-Y., & Shu, F. H. 1997, ApJ, 475, 237 NASA ADS
Lizano, S., & Shu, F. H. 1989, ApJ, 342, 834 NASA ADS
Looney, L. W., Mundy, L. G., & Welch, W. J. 2000, ApJ, 529, 477 NASA ADS
Loren, R. B., Sandqvist, A. A., & Wootten, A. 1983, ApJ, 270, 620 NASA ADS
Lucas, P. W., & Roche, P. F. 1997, MNRAS, 286, 895 NASA ADS
Lucas, P. W., & Roche, P. F. 1998, MNRAS, 299, 699 NASA ADS
Lynds, B. T. 1962, ApJS, 7, 1 NASA ADS
MacLeod, J., Avery, L., Harris, A., Tacconi, L., & Shuster, K. 1994, JCMT Newsletter, 3, 46
Masunaga, H., & Inutsuka, S. 2000, ApJ, 531, 350 NASA ADS
Masunaga, H., Miyama, S. M., & Inutsuka, S. 1998, ApJ, 495, 346 NASA ADS
Matzner, C. D., & McKee, C. F. 2000, in press
McCaughrean, M. J., Rayner, J. T., & Zinnecker, H. 1994, ApJ, 436, L189 NASA ADS
McLaughlin, D. E., & Pudritz, R. E. 1996, ApJ, 469, 194 NASA ADS
McLaughlin, D. E., & Pudritz, R. E. 1997, ApJ, 476
Miroshnichenko, A., Ivezic, Z., Vinkovic, D., & Elitzur, M. 1999, ApJ, 520, 115
Motte, F., André, P., & Neri, R. 1998, A&A, 336, 150 (MAN98) NASA ADS
Motte, F., Gueth, F., André, P., Dutrey, A., Guilloteau, S., & Neri, R. 2001, in preparation
Mouschovias, T. Ch. 1991, in The Physics of Star Formation and Early Stellar Evolution, ed. Lada, & Kylafis, 449
Myers, P. C. 1987, in Star forming regions, IAU Symp. 115, ed. M. Peimbert, & J. Jugaku, 33
Myers, P. C. 1998, ApJL, 496, L109 NASA ADS
Myers, P. C., & Benson, P. J. 1983, ApJ, 266, 309 NASA ADS
Myers, P. C., & Fuller, G. 1992, ApJ, 396, 631 NASA ADS
Myers, P. C., & Ladd, E. F. 1993, ApJ, 413, L47 NASA ADS
Myers, P. C., Fuller, G. A., Mathieu, R. D., et al. 1987, ApJ, 319, 340 (M 87) NASA ADS
Myers, P. C., Adams, F. C., Chen, H., & Schaff, E. 1998, ApJ, 492, 703 NASA ADS
Mundt, R., Brugel, E. W., & Bührke, T. 1987, ApJ, 319, 275 NASA ADS
Neufeld, D. A., Lepp, S., & Melnick, G. J. 1995, ApJS, 100, 132 NASA ADS
Ohashi, N., Hayashi, M., Kawabe, R., & Ishiguro, M. 1996, ApJ, 466, 317 NASA ADS
Ohashi, N., Kawabe, R., Hayashi, M., & Ishiguro, M. 1991, AJ, 102, 2054 NASA ADS
Ossenkopf, V., & Henning, Th. 1994, A&A, 291, 943 NASA ADS
Padgett, D. L., Brandner, W., Stapelfeldt, et al. 1999, AJ, 117, 1490 NASA ADS
Parker, N. D. 1988, MNRAS, 235, 139 NASA ADS
Penston, R. B. 1969, MNRAS, 144, 425 NASA ADS
Reipurth, B., Chini, R., Krügel, E., Kreysa, E., & Sievers, A. 1993, A&A, 273, 221 NASA ADS
Safier, P. N., McKee, C. F., & Stahler, S. W. 1997, ApJ, 485, 660 NASA ADS
Sandell, G., Aspin, C., Duncan, W. D., Russell, A. P. G., & Robson, E. I. 1991, ApJ, 376, L17 NASA ADS
Sandell, G., Knee, L. B. G., Aspin, C., Robson, I. E., & Russell, A. P. G. 1994, A&A, 285, L1 NASA ADS
Saraceno, P., André, P., Ceccarelli, C., Griffin, M., & Molinari, S. 1996, A&A, 309, 827 NASA ADS
Sonnhalter, C., Preibisch, Th., & Yorke, H. W. 1995, A&A, 299, 545 NASA ADS
Shirley, Y., Evans II, N. J., Rawlings, J. M. C., & Gregersen, E. M. 2000, in press
Shu, F. H. 1977, ApJ, 214, 488 NASA ADS
Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 NASA ADS
Shu, F. H., Shang, H., & Lee, T. 1996, Sci, 271, 1545 NASA ADS
Stahler, S. W. 1988, ApJ, 332, 804 NASA ADS
Tamura, M., Gatley, I., Waller, W., & Werner, M. W. 1991, ApJL, 374, L25 NASA ADS
Terebey, S., Chandler, C. J., & André, P. 1993, ApJ, 414, 759 NASA ADS
Terebey, S., Shu, F. H., & Cassen, P. C. 1984, ApJ, 286, 529 NASA ADS
Terebey, S., Vogel, S. N., & Myers, P. C. 1992, ApJ, 390, 181 NASA ADS
Terquem, C., Bertout, C. 1993, A&A, 274, 291 NASA ADS
Terquem, C., Bertout, C. 1996, MNRAS, 279, 415 NASA ADS
Tomisaka, K. 1996, PASJ, 48, L97 NASA ADS
Umemoto, T., Iwata, T., Fukui, Y., et al. 1992, ApJ, 392, L83 NASA ADS
Walker, C. K., Adams, F. C., & Lada, C. J. 1990, ApJ, 349, 515 NASA ADS
Ward-Thompson, D., Motte, F., & André, P. 1999, MNRAS, 305, 143 NASA ADS
Ward-Thompson, D., Scott, P. F., Hills, R. E., & André, P. 1994, MNRAS, 268, 276 NASA ADS
Whitworth, A., & Summers, D. 1985, MNRAS, 214, 1 NASA ADS
Wilking, B. A., Lada, C. J., & Young, E. T. 1989, ApJ, 340, 823 NASA ADS
Yun, J. L., & Clemens, D. P. 1991, ApJ, 381, 474 (YC91) NASA ADS
Yun, J. L., & Clemens, D. P. 1992, ApJ, 385, L21 NASA ADS

Online Material

$\begin{figure} \par\includegraphics[angle=270,width=17.5cm,clip]{ms10015f9ab.eps}\par\includegraphics[angle=270,width=17.5cm,clip]{ms10015f9cd.eps}\end{figure}$

Figure 9: Complement to Fig. 1. On-the-fly 1.3 mm continuum maps of Taurus embedded YSOs smoothed to a $13\hbox {$^{\prime \prime }$ }$ angular resolution. The positions of YSOs with weak emission are marked by star symbols. Contour levels and rms noise at map center are: a) 17 to 136 by 17 mJy/beam, $1\sigma \simeq 5$ mJy/beam; b) 20 40 mJy/beam, $1\sigma \simeq 6\$ mJy/beam; c) 25 to 100 by 25 mJy/beam, $1\sigma \simeq 6.5$ mJy/beam; d) 20 to 100 by 20 mJy/beam, $1\sigma \simeq 6.5$ mJy/beam

$\begin{figure} \par\includegraphics[angle=270,width=18cm,clip]{ms10015f10abcd.eps}\par\includegraphics[angle=270,width=18cm,clip]{ms10015f10efg.eps}\end{figure}$

Figure 10: Complement to Fig. 2. On-the-fly 1.3 mm continuum maps of several isolated globules (a- d) and Perseus protostars (e- g) (all smoothed to a $13\hbox {$^{\prime \prime }$ }$ effective beam). Starless fragments are marked by cross symbols. Contour levels and rms noise at map center are: a) 40 to 160 by 40 mJy/beam, $1\sigma \simeq 11$ mJy/beam; b) 90, 180, 270 mJy/beam, $1\sigma \simeq 26$ mJy/beam; c) 75, 150, 225 mJy/beam, $1\sigma \simeq 22$ mJy/beam; d) 35 to 245 by 35 mJy/beam, $1\sigma \simeq 9.5$ mJy/beam; e) 75 to 600 by 75 mJy/beam and 700 to 1500 by 100 mJy/beam, $1\sigma \simeq 22$ mJy/beam; f) 75 to 300 by 75 mJy/beam and 450 600 by 750 mJy/beam, $1\sigma \simeq 21$ mJy/beam; g) 0.2 to 1 by 0.2 Jy/beam and 1.5, 2, 3, 4 Jy/beam, $1\sigma \simeq 55$ mJy/beam

$\begin{figure} \par\includegraphics[angle=270,width=17.4cm,clip]{ms10015f11abcd.... ...par\includegraphics[angle=270,width=17.4cm,clip]{ms10015f11efgh.eps}\end{figure}$

Figure 11: Complement to Fig. 3. Radial intensity profiles of the environment of 12 Taurus embedded YSOs (a-l) and 4 starless cores (m-p). Column density estimates assuming $\k13=0.01\;\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ and $\mbox{$T_{\mbox{\tiny dust}}$ }=15\$ K are shown on the right axis of each profile (in m-p: $\k13=0.005\;\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ and $\mbox{$T_{\mbox{\tiny dust}}$ }=10\$ K). The observed profiles (solid curves) are compared with simulated model profiles (dotted curves) and with the 30 m beam (dashed curve). In b,c), e) and i), two source profiles are shown, before (upper solid curve) and after (lower solid curve) subtraction of the disk component observed by the IRAM Plateau de Bure interferometer at 1.4 mm (Motte et al. 2001); the latter should correspond to the profile of the envelope alone. The input models are all circularly symmetric with infinite power-law profiles, $I(\theta )\propto \theta ^{-m}$ . Unlike YSO envelope profiles, the profiles of starless cores (in m-p) are not consistent with single power-law models

$\begin{figure} \par\includegraphics[angle=270,width=17.4cm,clip]{ms10015f11ijkl.... ...ar\includegraphics[angle=270,width=17.4cm,clip]{ms10015f11mnop.eps} \end{figure}$

Figure 11: continued

$\begin{figure} \par\includegraphics[angle=270,width=17.5cm,clip]{ms10015f12abcd.... ...par\includegraphics[angle=270,width=17.5cm,clip]{ms10015f12efgh.eps}\end{figure}$

Figure 12: Complement to Fig. 4. Radial intensity profiles of the environment of 3 isolated IRAS globules (a-c), 4 Perseus protostars (e-h), and 1 starless core (d). Column density estimates assume $\k13=0.01\;\mbox{$\mbox{cm}^{2} \, \mbox{g}^{-1}$ }$ and $\mbox{$T_{\mbox{\tiny dust}}$ }=20$ K. In f-h), two source profiles are shown, before (upper solid curve) and after (lower solid curve) subtraction of the disk component observed by the IRAM PdBI interferometer at 1.4 mm (Motte et al. 2001). Unlike YSO envelope profiles, the profile of the starless core B361-NH3 (in d) is not consistent with a single power-law model