| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347100 | |
| Published online | 06 December 2023 | |
NAROO program
Precovery observations of potentially hazardous asteroids★
1
Institut Polytechnique des Sciences Avancées IPSA,
63 bis Boulevard de Brandebourg,
94200
Ivry-sur-Seine, France
e-mail: anne-charlotte.perlbarg@ipsa.fr
2
IMCCE, Observatoire de Paris, Université PSL, Sorbonne Université, Univ Lille, CNRS,
77 avenue Denfert-Rochereau,
75014
Paris, France
e-mail: anne-charlotte.perlbarg@obspm.fr
Received:
5
June
2023
Accepted:
1
August
2023
Context. The New Astrometric Reduction of Old Observations (NAROO) program is dedicated to the measurement of astrophotographic plates and the analysis of old observations for scientific purposes. One of the objectives of the NAROO program is to provide accurate positional measurements of small Solar System bodies in order to improve our knowledge of their orbits and dynamics.
Aims. Focused on potentially hazardous asteroids (PHAs), which are near-Earth asteroids (NEAs) making very close encounters with the Earth, this paper aims to emphasize the value of old photographic plate observations. As they provide accurate astrometric measurements over a large time interval, such observations are essential to determine reliable orbits and to detect small accelerations, such as the Yarkovsky effect.
Methods. Photographic plates consist of a substantial source of old observations of Solar System objects. From existing databases, we identified old and precovery observations of PHAs, which are fortuitous observations made before their discovery. We used the NAROO machine to digitize the plates, and we performed the astrometric reduction with the Gaia DR3 reference star catalog. We added the results to the observation dataset of PHAs in order to determine new orbital solutions and possibly detect the Yarkovsky effect with the Numerical Integration of the Motion of an Asteroid (NIMA) program. In addition, we considered a possible timing error in the orbit adjustment, which is generally not taken into account in such problems, and show its influence.
Results. We were able to find precovery observations of PHAs in photographic plate databases. Their introduction in the dataset show a significant improvement of the accuracy of the new orbital solutions. They also help in detecting and measuring the Yarkovsky effect and improve its accuracy. Hence, we demonstrate the interest of the reduction or new reduction of old photographic plates for the orbit determination of PHAs.
Key words: minor planets, asteroids: general / astronomical databases: miscellaneous / astrometry / ephemerides
Tables 2–4 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/680/A41
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The New Astrometric Reduction of Old Observations (NAROO)1 facilities have been built as a unique center dedicated to the measurement of astrophotographic plates and the analysis of old observations for scientific purposes (Robert et al. 2021). The framework is the study of the dynamics of Solar System bodies, in particular, those that require astrometric observations sampled over a long time span to quantify the long period terms that may help analyze the evolution of the motion of moving objects. One of the objectives of the NAROO program is to provide accurate positional measurements of small Solar System bodies in order to improve our knowledge of their orbits and dynamics.
Asteroids are small bodies in the Solar System composed of rocks, metal, and ice. Their size varies from a few meters to several hundred kilometers. In addition, some asteroids have an orbit that is close to that of the Earth, and any asteroid with a perihelion less than 1.3 au is considered a near-Earth asteroid (NEA). More than 3000 NEAs have been discovered each year since 2020, for a total of more than 30 000 as of 2023. Their dynamics are usually not very well known, as these objects are faint and are animated by nongravitational perturbations. Within the NEAs, those with very close encounters with the Earth are referred to as potentially hazardous asteroids (PHAs). By definition, they have an absolute magnitude below 22, which corresponds to a size of over 140 meters, depending on the albedo. They also have a minimum intersection orbit distance (MOID) with the Earth below 0.05 au, which is equivalent to 20 lunar distances (LDs). The PHAs represent a risk for the Earth since an impact with such objects may have catastrophic consequences. Thus, the knowledge of their dynamics and impact probability is essential.
Accurate astrometric measurements acquired over a large time span are essential to providing reliable orbits and to detecting small accelerations of such objects, and the photographic plates acquired over most of the 20th century comprise a substantial source of old observations of Solar System objects. Among the collection available at the Paris Observatory, we chose to focus on PHAs for orbit determination of threatening objects as a proof of concept, because of the potential improvement in their orbit, with practical applications assessing its feasibility and limits. First, available databases allow us to identify both old and precovery observations of PHAs, which represent fortuitous observations made before their discovery. Second, the NAROO program enables the digitization of photographic plates as well as astrometric reduction with the Gaia DR3 reference stellar catalog (Gaia Collaboration 2021). In this context, a new observation dataset of PHAs complemented with precovery observations will help refine orbital solutions and detect the Yarkovsky effect (Desmars 2015).
In Sect. 2, we introduce the available photographic plate databases that we used to identify precovery observations, and we describe their analysis. We also define the observation precision model developed to refine the orbital solution. In Sect. 3, we present the positioning results and contribution in a new dataset and hence the definition of new orbital solutions. Finally, we analyze the influence of these precovery astrometric observations on the detection and measurement of the Yarkovsky effect.
2 Methods
2.1 Photographic plates
The main sources of old observations of Solar System objects, including PHAs, are collections of photographic plates archived in observatories worldwide. The observations were realized on photographic plates (Fig. 1), which consist of glass plates covered with a photosensitive emulsion for a specific wavelength. The photographic plates were put in a dedicated system behind the eyepiece of a telescope, then set during a specific exposure time while following the observed object. The light hitting the emulsion created a chemical reaction that darkened the area, thus producing the negative of the observation. The negative was then immersed in different chemical baths to stop and fix the emulsion. The metadata of the observations, such as the designation of the instrument, the plate number, the date and time, the exposure time, the right ascension and declination of the center of the plate, and the emulsion, were generally recorded on the protective envelope of the plate or in a notebook. However, plates are very fragile and require specific storage conditions, including controlled temperature and humidity, in archive rooms so as not to become altered (Hendriks & Lesser 1983; Eastman Kodak Company 1967).
Photographic plates were used by astronomers from roughly 1890 to 1990 before being replaced by numerical devices like CCDs. These past observations are a treasure trove. Thousands were produced, but only a few subsets were analyzed for the needs at these epochs with former and manual methods. The observations realized for the astrometry of known Solar System objects have been reduced thanks to plate measuring instruments and former star catalogs. However, the positions extracted have large uncertainties and biases because of many error sources during the process of reduction (calibration and systematic errors). Today, we are able to make a new reduction of such observations thanks to the Gaia reference star catalog (Gaia Collaboration 2021) and the NAROO program (Robert et al. 2021). Indeed, the Gaia catalogs and their astrometric precision in the position, proper motion, parallax, and radial velocities of the reference stars allow for their position in time to be propagated with an uncertainty of less than 1 mas over a century, up to magnitude 20. Whereas the previous catalogs did not permit going back in time prior to the 1960s, due to their positioning accuracy, the latest Gaia release has finally solved this problem. Now, all the old observations can be analyzed with unprecedented precision, making all the data published when they were made obsolete today. In fact, precise digitization and new astrometric reduction of the old photographic plates provide very accurate positions (Robert et al. 2011, Robert et al. 2015, Robert et al. 2016), and their reprocessing even provide astrometric accuracy that is comparable to what is derived from space missions themselves (Robert et al. 2015). Astronomical observatories worldwide preserve thousands of photographic plates in their archives. Some of them have begun to inventory these materials with corresponding metadata in digital databases, thus allowing a more rigorous exploitation with today’s knowledge and technologies.
 |
Fig. 1 Photographic plate from the Palomar Observatory Sky Survey II showing the Andromeda Galaxy in the top-right corner. |
2.2 Plate databases
Our study is based on various collections of photographic plates available within the NAROO program at the Paris Observatory. In particular, we collaborated with the Observatoire de la Côte d’Azur (OCA) to work on two large collections of photographic plates of Solar System objects. The first collection contains plates realized between 1978 and 1996 with the Schmidt telescope of OCA-Calern (Caussols, France, IAU code 010), with a diameter of 1.52 m and a focal of 3.16 m. The collection is composed of about 3600 plates of 30 × 30 cm, corresponding to a field of view of about 5 × 54 degrees, with long exposure times in the range of 30–60 min. The second collection contains plates realized between 1935 and 1983 with the double Zeiss Astrograph of OCA-Nice (Nice, France, IAU code 020), with a diameter of 0.40 m and a focal of 2.00 m. This collection is composed of about 8200 plates of 9 × 12 cm to 18 × 24 cm in size, corresponding to a field of view of about 5 × 5 degrees, with short exposure times in the range of 5–20 min. We also collaborated with the Laboratoire d’Astrophysique de Bordeaux (LAB). Its collection contains plates realized between 1937 and 1996 with the Équatorial Photographique and Grand Équatorial of the Observatoire Astronomique de Bordeaux (Bordeaux, France, IAU code 999), with a diameter of 0.33 m and a focal of 3.43 m, and a diameter of 0.38 m and a focal of 6.82 m, respectively. The set is composed of about 4350 plates of 16 × 16 cm, corresponding to a field of view of about 4 × 4 degrees for the Équatorial Photographique and 2 × 2 degrees for the Grand Équatorial, with short exposure times in the range of 5–20 min (Jaschek 1984; Soulie et al. 1981).
Additionally, we worked on three collections of photographic plates of sky surveys in the archives of the Paris Observatory. The first collection contains plates from the Northern Palomar Observatory Sky Survey I (POSSI) realized between 1949 and 1958 with the Oschin Schmidt telescope of the Palomar Observatory (USA, IAU code 261), with a diameter of 1.22 m and a focal of 3.06 m. It is composed of about 2070 plates of 35 × 35 cm, corresponding to a field of view of about 6 × 6 degrees, with long exposure times in the range of 20–60 min (Minkowski & Abell 1963). The second collection contains plates from the Northern Palomar Observatory Sky Survey II (POSSII) realized with the same instrument and at the same place from 1985 to 2000. It is composed of about 1780 plates of 35 × 35 cm, corresponding to a field of view of about 6 × 6 degrees, with long exposure times of about 60 min (Reid et al. 1991). The third collection contains plates from the southern sky survey of the European Southern Observatory (ESO) and the United Kingdom Science and Engineering Research Council (SERC) realized with the ESO Schmidt telescope of La Silla Observatory (Chile, IAU code 809), with a diameter of 1.62 m and a focal of 3.06 m, from 1973 to 1990. It is composed of about 2440 plates of 30 × 30 cm, corresponding to a field of view of about 5 × 5 degrees, with long exposure times in the range of 60–120 min (Schuster & West 1988).
We analyzed the 22 440 photographic plates in the series using Sky Body Tracker (SkyBoT; Berthier et al. 2006) to identify the Solar System objects potentially observed. SkyBoT operates with a database of ephemerides of all objects in the Solar System over a time interval from 1889 November 13 to 2060 March 21. In particular, the SkyBoT Cone Search2 method allows objects in the field of view of our observations at a corresponding date, time, and location to be theoretically situated. Thus, we identified 5193 NEAs, 2 304264 main belt asteroids, 8714 Centaurs, and 219 trans-Neptunian objects. We verified that it is pointless to detect a moving object fainter than magnitude 20, and we identified only a few moving objects brighter than magnitude 20, and only among the more sensitive plates.
We chose to focus on PHAs and orbit determination of threating objects as a proof of concept, and we provide practical applications assessing its feasibility and limits. We were also looking to confirm the possibility of recovering not only old observations but also precovery observations of these objects as well. We define old observations as those made before the arrival of the Gaia catalog and precovery observations as fortuitous observations realized before the official discovery of an object. The key point is that we found both of them, and we decided to focus on precovery observations in order to emphasize the importance of their contribution in dataset. We selected ten PHAs with precovery observations that were candidates for the detection of the Yarkovsky effect: (175706) 1996 FG3; 2003 VE1; (99942) Apophis; (292220) 2006 SU49; (341843) 2008 EV5; 2013 NJ10; 2014 WV363; 2015 OL35; 2015 TE323; and (506074) Svarog. Table 1 shows the distribution of the precoveries in the plate collections. We detected precoveries in the databases of OCA Caussols, POSSI, POSSII, and ESO/SERC with long exposure times, but none in the databases of OCA Nice and LAB with short exposure times.
There is a difference between the number of our ten candidates for the detection of the Yarkovsky effect and the predicted number of 100 candidates given by Desmars (2015) and Robert et al. (2021). Actually, this theoretical result was estimated from the analysis of more complete databases of photographic plates. Though the plates available at Paris Observatory are numerous, they are not enough to ensure the same conditions of analysis, and we would face long unavoidable processing times if materials were to be loaned for collection completion. In this work, we thus present a first application showing that precovery data is something that cannot be guaranteed.
Detected precovery observations of PHAs in collections of photographic plates.
2.3 Digitization and analysis
The NAROO program (Robert et al. 2021) is dedicated to the digitization and the analysis of old astronomical observations with photographic plates. The digitizations are realized with a high precision digitizer in a temperature and humidity stabilized ISO-5 clean room to ensure the best digitizing conditions. The NAROO machine is composed of a high-resolution sCMOS camera on the Z axis and a plate holder mounted on an air-bearing XY positioning table. The whole system is supported by a granite based and vibrations are corrected thanks to dynamic feet. Glass plates up to 35 cm wide can be digitized. The resulting digitization has an accuracy better than 65 nm (corresponding to 1 to 5 mas, depending on the material) for the measurements, provided as a digital positive image in FITS format.
The photographic plates containing confirmed precoveries were brought to the NAROO facilities to be digitized and analyzed. The different steps of the digitization process are as follows: To begin, the glass side of the plate was cleaned with alcohol to remove such things as fingerprints and molds. Obviously, the other side could not be cleaned, as it would remove the emulsion and thus the observation. Both sides were dusted with an electrostatic microfiber cloth. Then, the trail of the asteroid was located on the plate and a line was drawn on the glass side so that it could be found again easily, as the plates could be large. We also compared the theoretical direction of the object with the direction of the trail to confirm that our observation matched the corresponding asteroid before digitization. Figure 2 is a typical example of a NAROO digitization. The trail of the asteroid is circled in red. The stains visible on the digitization correspond to the texture of the emulsion on the photographic plate, as the digitization is very fine. This figure shows the oldest precovery observation that we could find for our study; it was realized 60 yr before the discovery of 2014 WV363.
We used the Source-Extractor (SExtractor) software (Bertin & Arnouts 1996) to detect and measure the object positions on the image. We chose suitable extraction parameters for digitized observations to recover, for each source, all data for the astrometric reduction, including the x and y positions of the centroid with associated error, the full width half maximum, elongation, and photometric magnitude. Thereafter, we measured the x and y positions on the image of the beginning and the ending of the asteroid trail using the SAO Image DS9 software (Joye & Mandel 2003). We chose this method to preserve the information of velocity and technically because most of the trails were barely measurable and difficult to detect by fitting with an elongated point spread function using available software. As shown in Fig. 3, we fit a vector region on the asteroid trail of a size theoretically defined by the observation metadata and asteroid ephemeris. The end circle regions with a width defined by that of the trail were used to adjust the vector region to the trail extremities. With this method, the accuracy is within one pixel, but the extraction software could not provide any positions, as most trails were too faint for it. Finally, the astrometric reduction was performed using the method in Robert et al. (2011) with the Gaia DR3 reference stars for the image calibration.
The precision of the observations measured with the NAROO machine depends on the precision of the measurement, the quality of the plate, and the accuracy of the astrometric reduction. In addition, we took into account an uncertainty coming from the imprecise timing of the plate. In fact, the plate metadata indicate the timing at the minute level, whereas a second-level precision is required to fully exploit the observations, especially since asteroids are fast objects. In this context, we tried to refine the timing of the observations through two approaches. First, we identified main belt asteroids on plates that have a well-known orbit. We measured their position to verify whether their residuals could be minimized by changing the timing, without success. Hence, we decided to work on a second approach where we took into account the minute-level precision in the timing of the observation, which degrades the full precision of the observation. We developed a specific weighting scheme for these observations using a nondiagonal covariance matrix, assuming that the uncertainty ellipse is along the apparent motion. We adopted the Gaia formalism (Gaia Collaboration 2018) with the along-track (AL) coordinate, which is along the apparent direction of the asteroid, and the across-track (AC) coordinate, which is orthogonal to the AL (Fig. 4). This method led to a covariance matrix of the observation in the classical (RA, Dec) spherical coordinate system that is nondiagonal. The parameters determined with this approach were later used for the orbit fitting (Sect. 3.3).
We defined the position angle θ as the angle between the North pole and the apparent motion direction. We assumed that the covariance matrix is diagonal with respective variances in AL and AC:
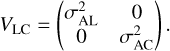 (1)
(1)
This allowed us to take into account the uncertainty in time and the apparent velocity of the asteroid in the variance of AL. We then detailed the quadratic sum 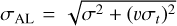 with σ the error of measure, σt the error in time, and υ the apparent velocity of the object. While the general formalism for the inversion’s algorithm is not modified by such an approach, the two end points of the trail are treated as independent measures. This is a conservative approximation that generally increases the timing uncertainties. A future study will quantify this effect of the timing uncertainty and correlation more clearly.
with σ the error of measure, σt the error in time, and υ the apparent velocity of the object. While the general formalism for the inversion’s algorithm is not modified by such an approach, the two end points of the trail are treated as independent measures. This is a conservative approximation that generally increases the timing uncertainties. A future study will quantify this effect of the timing uncertainty and correlation more clearly.
In the (RA, Dec) spherical coordinate system, the covariance matrix can be expressed as
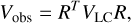 (2)
(2)
The covariance matrix becomes
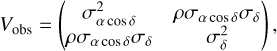 (4)
(4)
and the correspondence between σα cos δ, σδ, and 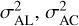 , and the correlation coefficient ρ is
, and the correlation coefficient ρ is
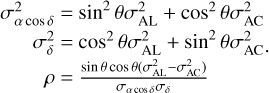 (5)
(5)
As an example, we provide the covariance matrix of the observation of 2014 WV363 from 1954 October 03 (06:18:00). At this date, the apparent motion derived from the ephemeris is µRA* = 5.21 arcsec h−1 and µDE = 141.07 arcsec h−1. It corresponds to an apparent velocity of υ = 141.17 arcsec h−1 and θ = 2.11 deg. The plate measurements give an estimated measure error of σα cos δ* = 0.240 arcsec and σδ* = 0.215 arcsec, so 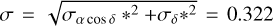 . For this plate, the uncertainty in time is σt = 60 s. Finally, we deduced that
. For this plate, the uncertainty in time is σt = 60 s. Finally, we deduced that 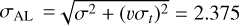 arcsec and σAC = σ = 0.322 arcsec.
arcsec and σAC = σ = 0.322 arcsec.
 |
Fig. 2 Digitization of the precovery observation of 2014 WV363 realized on 1954 October 03 at 06:18:00 UT, Palomar Observatory, POSSI photographic plate SO17. |
 |
Fig. 3 Determination of the beginning and the ending of the trail-by-trail adjustment with the theoretical direction and length of the object. |
 |
Fig. 4 Correspondence between spherical coordinates and AL/AC Gaia formalism. |
2.4 Dynamical model
The majority of PHAs were discovered in the 1990s thanks to different surveys dedicated to the detection and the tracking of near-Earth objects (NEOs). The monitoring of these objects started with the Palomar Planet-Crossing Asteroid Survey (PCAS; Helin & Shoemaker 1979), from 1973 to 1995. Today, the major contributors are the Lincoln Near-Earth Asteroid Research (LINEAR; Viggh et al. 1997), since 1996; the Catalina Sky Survey (CSS; Larson et al. 1998), since 1998; and the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS; Chambers 2009), since 2009. The sample of available observations (the adjustment period) of these bodies spans only for a short period. The accuracy of the positioning is generally of good quality during the adjustment period, but it deteriorates outside this period. Moreover, orbital solutions are more accurate over long adjustment periods, though it also depends on the observation quality (Desmars et al. 2013). Figure 5 illustrates the consequences of this point. The red dots in the figure denote the measured positions of one of the precovery observations of 2014 WV363 at the beginning and at the ending of the trail, while the blue dots denote the theoretical positions of the asteroid at the beginning and at the ending of the trail, which were calculated over an adjustment period (2011–2019) that did not include our precovery observation. A comparison between both position sets showed a difference of about 10 arcsec due to the lack of astrometric positions at this period in orbit computation. In this context, the value of precovery observations acquired over a large time span seems to be essential to providing reliable orbits and measuring small accelerations, namely, the Yarkovsky effect.
Orbits of PHAs are numerically determined from dynamical models fitted to observations. Although, several models exist for the same object, they differ by the perturbations and corrections introduced and on the numerical method used to integrate the equations of motion. For example, OrbFit (Orbfit Consortium 2011) is a software for computing orbits from observations, propagating orbits, and computing positions. That being said, we chose to use the Numerical Integration of the Motion of an Asteroid (NIMA) software (Desmars 2015), which is equivalent to OrbFit, mainly because we were allowed to modify its source code for our needs by including the timing error in the adjustment. The NIMA software allows for the determination of the asteroid orbital solutions from observations by computing orbital elements, and it generates ephemerides. The program is based on the numerical integration of the equations of motion with a Gauss-Radau method (Everhart 1985) and of the variational equations with a Levenberg-Marquardt algorithm. The modeling takes into account the gravitational perturbations caused by the Sun, the Moon, the planets, and Pluto, using INPOP19a planetary ephemerides (Fienga et al. 2019), and the largest asteroids of the main belt preliminary, computed with NIMA (Ceres, Pallas, Vesta and Hygiea), as well as the correction of the relativistic effects. The theoretical dynamical model is fit to the astrometric measurements (radar, observations) available at the MPC. We used the weighting scheme detailed by Desmars et al. (2015), who derived the estimated precision of the observation from Farnocchia et al. (2015) depending on the date, the observatory location, the stellar catalog used for the astrometric reduction, and the number of observations realized during the same night and in the same observatory. The resulting initial state vector allowed us to define the orbital elements and thus the orbital solution of the object that will be used to calculate its ephemeris.
 |
Fig. 5 Comparison between the theoretical position of the trail in blue and the measured position of the trail in red of 2014 WV363 over the exposure time from 1954 October 03 at 06:18:00 UT to 06:28:00 UT, Palomar Observatory, POSSI photographic plate SO17. |
Measured positions of selected PHAs on photographic plates from Caussols (010), Palomar (261), and La Silla (809) observatories.
3 Results
3.1 Asteroid positions
Table 2 summarizes the precovery positions measured on the selected photographic plates. We measured the beginning and the ending positions for all the PHAs except for the ending position of 2003 VE1, as the trail ended outside of the plate. The columns in the table correspond to the object; the UT date and time; the observed right ascension and declination (ICRF) in hour, minute, second and degree, arcminute, arcsecond, respectively; the IAU observatory code; the covariance matrix error on both spherical coordinates in arcseconds; the correlation coefficient; and the measurement error on both coordinates in arcseconds.
3.2 Method validation
To validate our method and full treatment chain, we worked on observations of (4179) Toutatis because its orbit is well determined. As of 2023 April 23, 6655 observations (1934–2023), 63 radar measurements (1992–2017), and 75 direct observations by Gaia (2016–2017) are available at the MPC. On our side, we found eight plates from the database of OCA Caussols (1989– 1993) and POSSII (1997). The new reduced observations will not help refine the orbit, but they will help validate our method. Although the observations from OCA Caussols in 1989 and POSSII in 1997 were already present in the MPC database, they were analyzed with a former technique and reference star catalog that we replace by our measurements for the analysis. Notably, observations from OCA Caussols in 1993 were completely original and had never been analyzed before. Table 3 shows 16 astrometric observations deduced from the corresponding photographic plates. The columns correspond to the object; the UT date and time; the observed right ascension and declination (ICRF) in hour, minute, second and degree, arcminute, arcsecond, respectively; the IAU observatory code; the covariance matrix error on both spherical coordinates in arcseconds; the correlation coefficient; and the measurement error on both coordinates in arcseconds.
Figure 6 (top) shows the comparison of the astrometric residuals in spherical coordinates between MPC and NAROO analyses for the 12 common observations in both databases. As expected, the NAROO analysis provides better residuals, but there is still a large discrepancy, particularly in right ascension, which could be due to uncertainties in the exact timing of the observations. To better assess this point, Fig. 6 (bottom) shows the astrometric residuals projected on the apparent velocity vector using AL/AC Gaia formalism. The residuals are better in AC with an average of µAC = 110 mas and standard deviation of σAC = 320 mas, whereas we found an average of µAL = 500 mas and standard deviation of σAL = 676 mas in AL. By comparison, the same dataset in MPC has the following statistics: µAC = 1548 mas and σAC = 3198 mas in AC, and µAL = −428 mas and σAL = 1565 mas in AL. The discrepancy in AL could again be due to uncertainties in the exact timing of the observations. In fact, when divided by the norm of the apparent velocity, residuals then correspond to several tens of seconds, which is a consequence of the minute-level precision of the timing. We may conclude that NAROO analyses allow for better positioning compared to previous ones (such as MPC), but we also highlight the consequence of uncertainties in the timing of observations. This also justifies our weighting scheme, taking into account a nondiagonal covariance matrix for the NAROO observations and the uncertainty in the timing.
Measured positions of (4179) Toutatis on photographic plates from Caussols (010) and Palomar (261) observatories.
 |
Fig. 6 Comparison of the astrometric residuals in spherical coordinates (top) and AL/AC coordinates (bottom) between MPC and NAROO analyses, in arcseconds, for (4179) Toutatis. |
3.3 Orbital solutions of PHAs
We added our precovery observations of PHAs to their corresponding position datasets available at the MPC. For example, asteroid 2014 WV363 was discovered on 2014 November 11, and its MPC observational period is 2011-2019. We found two precovery observations of this object, meaning four precovery positions in 1954. One position was not used, as the plate is hardly measurable, but we were nonetheless able to extend the observational period to 1954–2019. Figure 7 shows the uncertainty in angular distance of 2014 WV363, in arcseconds, over the period 1900–2100. Figure 8 shows the uncertainty in geocentric distance of 2014 WV363, in kilometers, over the period 1900–2100. The addition of the precovery measurements made a significant improvement in the ephemeris accuracy over the complete period, as both the uncertainty in angular distance and in geocentric distance decrease when these data are used. We concluded that a few precovery observations are enough to improve the accuracy of the dynamics and thus the orbit solution. We made the same conclusion for other objects, which is in agreement with our simulations in Robert et al. (2021).
Focusing on a specific object, Apophis represents an emblematic case for planetary defense. Today, its orbit is well constrained and any risk of collision has been ruled out for the 21st century, but this has not always been the case. The precovery observations allow us to extend the orbital period and provide a unique constraint. In the future, if a newly discovered object presents a non-zero risk of collision, a systematic search of past observations and a program like NAROO represent a unique tool for refining and constraining impact probabilities.
Measured positions of (152563) 1992 BF on photographic plates from the Palomar (261) Observatory.
Estimations of A2, drift in semi-major axis da/dt, and standard deviations for (152563) 1992 BF.
 |
Fig. 7 Uncertainty in angular distance of 2014 WV363, in arcseconds, over the period 1900–2100. Green points denote the propagation accuracy of the ephemeris using original astrometric observations available at the MPC. Purple points denote the propagation accuracy of the ephemeris with three precovery observations added in the dataset. |
 |
Fig. 8 Uncertainty in geocentric distance of 2014 WV363, in kilometers, over the period 1900–2100. Green points denote the propagation accuracy of the ephemeris using original astrometric observations available at the MPC. Purple points denote the propagation accuracy of the ephemeris with three precovery observations added in the dataset. |
3.4 Application to Yarkovsky effect
As presented in Desmars (2015), precoveries can be used to detect small accelerations in the motion of asteroids by extending the period of observation. In this context, the Yarkovsky acceleration is a small acceleration that produces a drift in the semi-major axis of small bodies. It can be modeled by a transverse force inversely proportional to the square of the distance (Marsden et al. 1973):
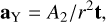 (6)
(6)
where r is the heliocentric distance to the asteroid and t is the transverse vector. The A2 parameter is determined within the orbital fitting as well as the state vector.
Precoveries have been used to constrain the Yarkovsky acceleration of (152563) 1992 BF in Vokrouhlický et al. (2008). The authors used photographic plates of POSSI from 1953 where the object is visible in order to derive a new astrometry and then measure the Yarkovsky effect. As the same plates are available in the NAROO database, we reanalyzed them to compare the results. Following the digitization, analysis, and reduction with the Gaia DR3 star catalog, we derived the astrometric positions of (152563) 1992 BF, given in Table 4. The columns in the table show the object; the UT date and time; the observed right ascension and declination (ICRF) in hour/minute/second and degree/arcminute/arcsecond, respectively; the IAU observatory code; the covariance matrix error on both spherical coordinates in arcsec; the correlation coefficient; and the measurement error on both coordinates in arcseconds. Using the original data given in Vokrouhlický et al. (2008) and more positions of the asteroid up to 2022, we first derived A2 = (−25.631 ± 2.205) × 10−15 au day−2. Then, by substituting the NAROO calculated positions, we derived A2 = (−26.415 ± 1.217) × 10−15 au day−2. Both results are in the same order of magnitude, but our new estimation has an improved accuracy by a ratio of about 45%. Table 5 provides a comparison of A2 and da/dt estimations from different orbital solutions.
The NAROO estimations appear to be better, mainly because of the quality of the digitization and the use of Gaia DR3 instead of USNO B2, which has zonal errors. As for the previous cases, the most important limitation comes from the uncertainty in timing, as revealed in Fig. 9. In fact, when divided by the norm of the apparent velocity, residuals then correspond to several tens of seconds, which is a consequence of the minute-level precision of the timing.
In addition, we tried to estimate the Yarkovsky acceleration with a reliable A2 parameter for all the precoveries given in Table 2. Table 6 provides a comparison of A2 and da/dt estimations without and with taking into account the precovery observations in orbital solutions. In most of the cases, taking into account the precovery observations allowed us to improve the accuracy of the estimation for both A2 and da/dt, with some exceptions. The estimations for (99942) Apophis did not change since its orbit is well known today. The cases of 2008 EV5 and 2015 OL35 are particular because their precoveries were rejected by the fitting program, and they do not provide reliable A2 in any case. The A2 parameter of 2013 NJ10 was not detectable without nor with precoveries. And, more interesting, the A2 parameter of 2003 VE1 became detectable. We thus demonstrate that using NAROO precovery observations helps estimate the Yarkovsky effect and improve its accuracy. This being said, there is a difference between our mean positioning accuracy of our observations of about 200 mas and those of 30 mas in Robert et al. (2021) that would have been necessary for the determination of the most precise drifts in semi-major axis. In fact, and in addition to the timing errors, we identified PHAs only on Schmidt plates that have a large field of view, decreasing the astrometric precision of all the sources, and that were not taken into account in the previous studies.
Estimations of A2, drift in semi-major axis da/dt, and standard deviations for selected PHAs, without and with their precovery observations.
 |
Fig. 9 Comparison of the astrometric residuals in spherical coordinates (top) and AL/AC coordinates (bottom) between MPC, Vokrouhlický et al. (2008), and NAROO analyses, in arcseconds, for (152563) 1992 BF. |
4 Conclusion
Old observations on photographic plates are a treasure trove since they compose a substantial source of observations of Solar System objects over a large time span. In this work, we were able to identify 10 PHAs with precovery and old observations in databases of such materials from various observatories. We also managed to digitize and analyze these past observations in the framework of the NAROO program and with the Gaia DR3 astrometric catalog.
The digitization of the photographic plates using the NAROO machine and the reduction or new reduction using the Gaia DR3 star catalog provided accurate astrometric measurements that are essential to determining reliable orbits. Introducing precovery observations in the dataset helped significantly improve the dynamics and thus the ephemerides. Moreover, they helped detect and constrain the Yarkovsky effect and improve its accuracy for several objects. We demonstrated the interest of a reduction or a new reduction of old photographic plates for orbit determination of PHAs. Such data, acquired in the framework of large programs, could be used to better assess the risk of PHAs in the context of planetary defense, space surveillance and tracking, or Space Situational Awareness.
Our analysis is an example of the capacities of the NAROO program, which is not limited to PHAs. Other populations of objects have been observed with photographic plates, including small bodies such as main belt asteroids, trans-Neptunian objects, comets, and planets. Corresponding databases are being studied with large collections to improve the object dynamics. Future applications will focus on specific targets in order to meet community needs, for example, space mission targets or future threatening PHAs.
Acknowledgements
This study shows outcomes from the NAROO program which was supported by the DIM-ACAV of Île-de-France region, PSL Research University, the Programme National GRAM (PNGRAM), the Programme National de Planétologie (PNP) and the Programme National Soleil-Terre (PNST) of CNRS/INSU with INP and IN2P3, co-funded by CNES, and the Gaia Specific Action (AF Gaia) of Paris Observatory. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. The authors are grateful to the archive and heritage commission of the OCA and the LAB.
References
- Berthier, J., Vachier, F., Thuillot, W., et al. 2006, ASP Conf. Ser., 351, 367 [NASA ADS] [Google Scholar]
- Bertin, E. & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, K. C. 2009, in Am. Astron. Soc. Meeting Abstracts, 213, 301.07 [NASA ADS] [Google Scholar]
- Desmars, J. 2015, A&A, 575, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmars, J., Bancelin, D., Hestroffer, D., & Thuillot, W. 2013, A&A, 554, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmars, J., Camargo, J. I. B., Braga-Ribas, F., et al. 2015, A&A, 584, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eastman Kodak Company 1967, Kodak plates and films for science and industry (Kodak Publication P-9) [Google Scholar]
- Everhart, E. 1985, in Astrophy. Space Sci. Lib., 115, IAU Colloq. 83: Dynamics of Comets: Their Origin and Evolution, eds. A. Carusi, & G. B. Valsecchi, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Chamberlin, A. B., & Tholen, D. J. 2015, Icarus, 245, 94 [Google Scholar]
- Fienga, A., Deram, P., Viswanathan, V., et al. 2019, Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste, 109 [Google Scholar]
- Gaia Collaboration (Spoto, F., et al.) 2018, A&A, 616, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helin, E. F., & Shoemaker, E. M. 1979, Icarus, 40, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Jaschek, C. 1984, Bulletin d’Information du Centre de Donnees Stellaires, 27, 197 [Google Scholar]
- Joye, W. A. & Mandel, E. 2003, in ASP Conf. Ser., 295, Astronomical Data Analysis Software and Systems XII, eds. H. E. Payne, R. I. Jedrzejewski, & R. N. Hook, 489 [NASA ADS] [Google Scholar]
- Hendriks, K. B., & Lesser, B. 1983, Am. Arch., 46, 52 [Google Scholar]
- Larson, S., Brownlee, J., Hergenrother, C., & Spahr, T. 1998, BAAS, 30, 1037 [NASA ADS] [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Yeomans, D. K. 1973, AJ, 78, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Minkowski, R. L., & Abell, G. O. 1963, in Basic Astronomical Data: Stars and Stellar Systems, ed. K. A. Strand, 481 [Google Scholar]
- Orbfit Consortium 2011, Astrophysics Source Code Library, [record ascl:1106.015] [Google Scholar]
- Reid, I. N., Brewer, C., Brucato, R. J., et al. 1991, PASP, 103, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Robert, V., de Cuyper, J. P., Arlot, J. E., et al. 2011, MNRAS, 415, 701 [Google Scholar]
- Robert, V., Lainey, V., Pascu, D., et al. 2015, A&A, 582, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robert, V., Pascu, D., Lainey, V., et al. 2016, A&A, 596, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robert, V., Desmars, J., Lainey, V., et al. 2021, A&A, 652, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuster, H. E. & West, R. M. 1988, The Messenger, 54, 28 [NASA ADS] [Google Scholar]
- Soulie, G., Dupouy, Teulet, Broqua, & Dulou, M. R. 1981, A&AS, 43, 147 [NASA ADS] [Google Scholar]
- Viggh, H. E. M., Stokes, G. H., Shelly, F. C., Blythe, M. S., & Stuart, J. S. 1997, in AAS/Division for Planetary Sciences Meeting Abstracts, 29, 03.02 [NASA ADS] [Google Scholar]
- Vokrouhlický, D., Chesley, S. R., & Matson, R. D. 2008, AJ, 135, 2336 [Google Scholar]
All Tables
Measured positions of selected PHAs on photographic plates from Caussols (010), Palomar (261), and La Silla (809) observatories.
Measured positions of (4179) Toutatis on photographic plates from Caussols (010) and Palomar (261) observatories.
Measured positions of (152563) 1992 BF on photographic plates from the Palomar (261) Observatory.
Estimations of A2, drift in semi-major axis da/dt, and standard deviations for (152563) 1992 BF.
Estimations of A2, drift in semi-major axis da/dt, and standard deviations for selected PHAs, without and with their precovery observations.
All Figures
 |
Fig. 1 Photographic plate from the Palomar Observatory Sky Survey II showing the Andromeda Galaxy in the top-right corner. |
| In the text | |
 |
Fig. 2 Digitization of the precovery observation of 2014 WV363 realized on 1954 October 03 at 06:18:00 UT, Palomar Observatory, POSSI photographic plate SO17. |
| In the text | |
 |
Fig. 3 Determination of the beginning and the ending of the trail-by-trail adjustment with the theoretical direction and length of the object. |
| In the text | |
 |
Fig. 4 Correspondence between spherical coordinates and AL/AC Gaia formalism. |
| In the text | |
 |
Fig. 5 Comparison between the theoretical position of the trail in blue and the measured position of the trail in red of 2014 WV363 over the exposure time from 1954 October 03 at 06:18:00 UT to 06:28:00 UT, Palomar Observatory, POSSI photographic plate SO17. |
| In the text | |
 |
Fig. 6 Comparison of the astrometric residuals in spherical coordinates (top) and AL/AC coordinates (bottom) between MPC and NAROO analyses, in arcseconds, for (4179) Toutatis. |
| In the text | |
 |
Fig. 7 Uncertainty in angular distance of 2014 WV363, in arcseconds, over the period 1900–2100. Green points denote the propagation accuracy of the ephemeris using original astrometric observations available at the MPC. Purple points denote the propagation accuracy of the ephemeris with three precovery observations added in the dataset. |
| In the text | |
 |
Fig. 8 Uncertainty in geocentric distance of 2014 WV363, in kilometers, over the period 1900–2100. Green points denote the propagation accuracy of the ephemeris using original astrometric observations available at the MPC. Purple points denote the propagation accuracy of the ephemeris with three precovery observations added in the dataset. |
| In the text | |
 |
Fig. 9 Comparison of the astrometric residuals in spherical coordinates (top) and AL/AC coordinates (bottom) between MPC, Vokrouhlický et al. (2008), and NAROO analyses, in arcseconds, for (152563) 1992 BF. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.